Игра «Жизнь» — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970 году. Это игра без игроков, в которой человек создаёт начальное состояние, а потом лишь наблюдает за её развитием. В игре можно создать процессы с полнотой по Тьюрингу, что позволяет реализовать любую машину Тьюринга.

Архитектура фон Неймана — широко известный принцип совместного хранения команд и данных в памяти компьютера. Вычислительные машины такого рода часто обозначают термином «машина фон Неймана», однако соответствие этих понятий не всегда однозначно. В общем случае, когда говорят об архитектуре фон Неймана, подразумевают принцип хранения данных и инструкций в одной памяти. Альтернативой архитектуре фон Неймана является гарвардская архитектура.

Кле́точный автома́т — дискретная модель, изучаемая в математике, теории вычислимости, физике, теоретической биологии и микромеханике. Основой является пространство из прилегающих друг к другу клеток (ячеек), образующих решётку. Каждая клетка может находиться в одном из конечного множества состояний. Решётка может быть любой размерности, бесконечной или конечной, для решётки с конечными размерами часто предусматривается закольцованность при достижении предела (границы). Для каждой клетки определено множество клеток, называемых окрестностью. Например, окрестность фон Неймана ранга 2 включает все клетки на расстоянии не более 2 от текущей. Устанавливаются правила перехода клеток из одного состояния в другое. Обычно правила перехода одинаковы для всех клеток. Один шаг автомата подразумевает обход всех клеток и на основе данных о текущем состоянии клетки и её окрестности определение нового состояния клетки, которое будет у неё при следующем шаге. Перед стартом автомата оговаривается начальное состояние клеток, которое может устанавливаться целенаправленно или случайным образом.

Алгори́тм волново́й трассиро́вки — алгоритм поиска пути, алгоритм поиска кратчайшего пути на планарном графе. Принадлежит к алгоритмам, основанным на методах поиска в ширину.

n-клетка — кубический граф обхвата n с наименьшим возможным числом вершин. Граф называется кубическим, если из каждой его вершины выходят 3 ребра. Обхват графа — это длина наименьшего цикла в нём.
Числа Деланнуа (или числа Деланоя; фр. Delannoy) D(a, b) в комбинаторике описывают количества путей из левого нижнего угла прямоугольной решётки (a, b) в противоположный по диагонали угол, используя только ходы вверх, вправо или вверх-вправо («ходом короля»). В a-мерном клеточном автомате D(a,b) задают количество клеток в окрестности фон Неймана радиуса b, последовательность A008288 в OEIS; количество клеток на поверхности окрестности задет последовательность A266213 в OEIS. Названы в честь французского математика Анри Огюста Деланнуа.

Фронтальный клеточный автомат - специальный тип вычислительных алгоритмов, основанных на моделях клеточных автоматов.
Теорией Ку́пмана — фон Не́ймана (KvN-теорией) в математической физике называется оригинальная переформулировка классической статистической механики, созданная американскими математиками Джоном фон Нейманом и Бернардом Купманом. Формализм механики Купмана — фон Неймана максимально приближен к формализму нерелятивистской квантовой механики: состояние динамической системы в ней описывается при помощи классической волновой функции, являющейся аналогом квантовомеханической волновой функции, классическое уравнение Лиувилля приобретает математическую структуру уравнения Шрёдингера и т. д.
Центрированное квадратное число — это центрированное полигональное число, которое представляет квадрат с точкой в центре и все остальные окружающие точки, находящиеся на квадратных слоях.

Джон фон Не́йман — венгеро-американский математик, физик и педагог еврейского происхождения, сделавший важный вклад в квантовую физику, квантовую логику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки.
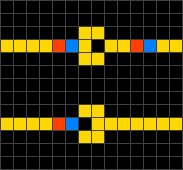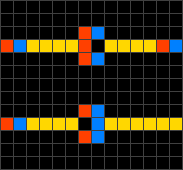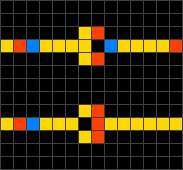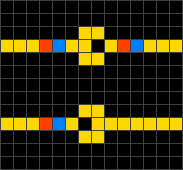
Wireworld — клеточный автомат, предложенный Брайаном Сильверманом в 1987 году, смоделированный в его программе Phantom Fish Tank. Автомат стал более известен после опубликования статьи в колонке «Computer Recreations» журнала Scientific American. Wireworld в особенности пригоден для симуляции электронных логических элементов, или «гейтов». Несмотря на простоту правил, Wireworld является полным по Тьюрингу.

Расстояние городских кварталов — метрика, введённая Германом Минковским. Согласно этой метрике, расстояние между двумя точками равно сумме модулей разностей их координат.

В теории графов смежной вершиной вершины v называется вершина, соединённая с v ребром. Окрестностью вершины v в графе G называется порождённый подграф графа G, состоящий из всех вершин, сопряжённых v и всех рёбер, соединяющих две такие вершины. Например, рисунок показывает граф с 6 вершинами и 7 рёбрами. Вершина 5 смежна вершинам 1, 2 и 4, но не смежна вершинам 3 и 6. Окрестность вершины 5 — это граф с тремя вершинами 1, 2 и 4, и одним ребром, соединяющим вершины 1 и 2.

Окре́стность Му́ра клетки — в двумерном случае — совокупность восьми клеток на квадратном паркете, имеющих общую вершину с данной клеткой. Окрестность получила своё название в честь одного из пионеров теории клеточных автоматов Эдварда Мура.
Натюрмо́рт — класс конфигураций в «Жизни» — созданной Конвеем модели клеточного автомата.

Эрнст Нейман, Франц Эрнст Кристиан Нейман — немецкий патолог и гематолог.
CW-комплекс — тип топологического пространства с дополнительной структурой, введённый Уайтхедом для удовлетворения нужд теории гомотопий. В литературе на русском языке употребляются также названия клеточное пространство, клеточное разбиение и клеточный комплекс. Класс клеточных комплексов является более широким, чем класс симплициальных комплексов, но в то же время сохраняет комбинаторную природу, которая позволяет производить эффективные вычисления.

HighLife — клеточный автомат, модификация игры «Жизнь». Придуман в 1994 году Нейтаном Томпсоном, назван Джоном Конвеем.
Проецирование в выпуклые множества, которое иногда упоминается как метод попеременного проецирования, является методом поиска точки в пересечении двух замкнутых выпуклых множеств. Это очень простой алгоритм и был переоткрыт много раз. Простой случай, когда множествами являются аффинные пространства, проанализировал Джон фон Нейман. Случай аффинных пространств является частным, поскольку итерации сходятся не просто к точке в пересечении, а к ортогональной проекции (исходной) точки на пересечение множеств. Для случая общих замкнутых выпуклых множеств предельная точка не обязательно будет проекцией. Классическая работа для случая двух замкнутых выпуклых множеств показывает, что скорость сходимости итераций линейна. Имеются расширения, в которых рассматриваются случаи более одного множества, или когда множества не выпуклы, или варианты, дающие более быструю сходимость. При анализе POCS и связанных методов пытаются показать, что алгоритм сходится, и выяснить, сходится ли метод к проекции исходной точки. Ответы, в основном, известны для простых случаев, но эта область активно исследуется в направлении обобщений. Есть два варианта алгоритма, таких как алгоритм Дикстры. См. ссылки в разделе «Литература для дальнейшего чтения» с обзором вариантов, обобщений и приложений метода POCS. Хорошее изложение истории метода можно найти в разделе III книги Комбета.
Алгоритм Дикстры — метод нахождения точки из пересечения выпуклых множеств. Является вариантом метода поочерёдного проецирования, известного также как метод проецирования в выпуклые множества. В простейшем варианте метод находит точку из пересечения двух выпуклых множеств путём итеративного проецирования в каждое из них. Метод отличается от метода поочерёдного проецирования наличием промежуточных шагов. Параллельную версия алгоритма разработали Гафке и Матар.