
Архиме́дово те́ло — выпуклый многогранник, имеющий в качестве граней два или более типов правильных многоугольников, примыкающих к идентичным вершинам. Здесь «идентичные вершины» означают, что для любых двух вершин существует изометрия всего тела, переводящая одну вершину в другую.

Окта́эдр — многогранник с восемью гранями.
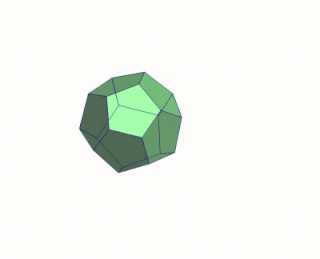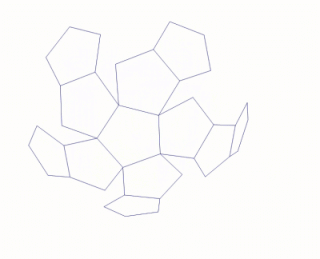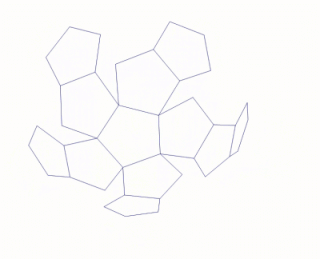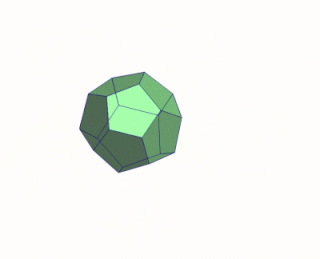
Развёртка многогранника — совокупность многоугольников, соответственно равных граням многогранника, с указанием того, какие стороны и вершины многоугольников соответствуют одним и тем же рёбрам и вершинам многогранника. Модели многогранников часто склеиваются из развёрток или отдельных многоугольников с указанием сторон, которые должны быть склеены.

Изгибаемый многогранник — многогранник, чью пространственную форму можно изменить непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров, а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника.

Ехидна́эдр — последняя звёздчатая форма икосаэдра, также называют полной или завершающей формой икосаэдра, так как она включает в себя все ячейки звёздчатой диаграммы икосаэдра.
Шестиугольная призма — призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин.

Усечение — операция в пространстве любой размерности, которая отсекает вершины многогранника и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.

Линк вершины многогранника или вершинная фигура — многогранник на единицу меньшей размерности, который получается в сечении исходного многогранника плоскостью, срезающей одну вершину. В частности линк вершины содержит информацию о порядке следования граней многогранника вокруг одной вершины.
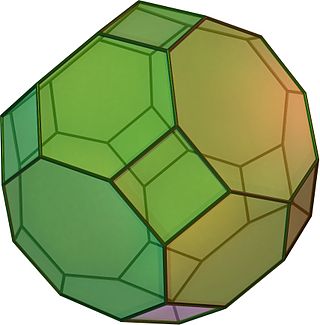
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию, усечённый кубооктаэдр является зоноэдром.
Соединение многогранников — это фигура, составленная из некоторых многогранников, имеющих общий центр. Соединения являются трёхмерными аналогами многоугольных соединений, таких как гексаграмма.

Звёздчатый октаэдр, или stella octangula, — единственная звёздчатая форма октаэдра. Латинским именем stella octangula многогранник назвал Кеплер в 1609, хотя он был известен более ранним геометрам. Так, он изображён в труде Пачоли De Divina Proportione, 1509.
Однородный многогранник — многогранник, грани которого являются правильными многоугольниками, и он вершинно транзитивен. Отсюда следует, что все вершины конгруэнтны, и многогранник имеет высокую степень зеркальной и вращательной симметрии.

Однородный звёздчатый многогранник — самопересекающийся однородный многогранник. Эти многогранники называются также невыпуклыми многогранниками, подчёркивая самопересечение. Каждый многогранник может содержать грани в виде звёздчатых многоугольников или иметь звёздчатые вершинные фигуры, но может содержать и то, и другое.

Образование звёздчатой формы — процесс расширения многоугольника, или многогранника в пространствах размерности 3 и выше с образованием новой фигуры.
Квазипра́вильный многогра́нник — полуправильный многогранник, который имеет в точности два вида правильных граней, поочерёдно следующих вокруг каждой вершины. Эти многогранники рёберно транзитивны, а потому на шаг ближе к правильным многогранникам, чем полуправильные, которые лишь вершинно транзитивны.
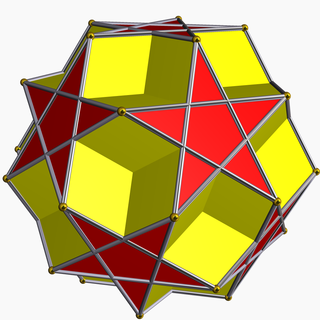
Додекододекаэдр — однородный звёздчатый многогранник, имеющий номер U36.

Многогранник Шёнхардта — простейший невыпуклый многогранник, который нельзя триангулировать тетраэдрами без добавления новых вершин. Многогранник назван именем немецкого математика Эриха Шёнхардта, построившего его в 1928 году.

Дельтаэдр — это многогранник, все грани которого являются правильными треугольниками. Название взято от греческой заглавной буквы дельта, которая имеет форму равностороннего треугольника. Существует бесконечно много дельтаэдров, но из них только восемь выпуклы, и они имеют 4, 6, 8, 10, 12, 14, 16 и 20 граней.
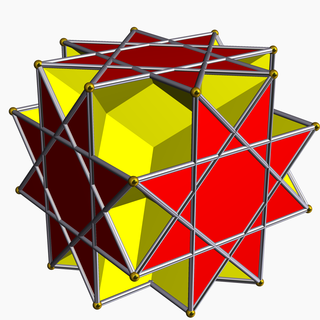
Большой ромбогексаэдр — невыпуклый однородный многогранник. Двойственным ему является большой ромбогексакрон. Вершинная фигура — самопересекающийся четырёхугольник.

Икосаэдр — это многогранник с 20 гранями.

















