Отбор признаков
Отбор признаков (отбор переменных, отбор атрибутов, отбор предикторов, реже — генерализация) — процесс отбора подмножества значимых признаков (как зависимых, так и независимых переменных) для построения модели в машинном обучении. Отбор признаков используется по четырём причинам:
- упрощение модели для повышения интерпретируемости[1]
- для сокращения времени обучения
- во избежание проклятия размерности
- улучшение обобщающей способности модели и борьба с переобучением[2].
Центральный посыл использования техники отбора признаков — наличие в данных излишних или незначимых признаков, которые могут быть удалены без существенной потери информации[2]. («Избыточность» и «незначимость» признаков — различные понятия, поскольку один значимый признак может быть излишним при присутствии другого значимого признака, с которым он сильно коррелирует[3].)
Отбор признаков следует отличать от выделения признаков. Выделение признаков создаёт новые признаки, как функции от оригинальных признаков, в то время как отбор признаков возвращает подмножество признаков. Техники отбора признаков часто используются в областях, где имеется много признаков и выборки сравнительно малы (мало точек данных). Классическими местами применения отбора признаков являются анализ рукописных текстов и ДНК-микрочипы, где имеются много тысяч признаков и от десятков до сотен экземпляров выборки.
Введение
Алгоритм отбора признаков можно рассматривать как комбинацию техник поиска для представления нового поднабора признаков вместе с вычислением меры, которая отражает различие подмножеств признаков. Простейшим алгоритмом является проверка каждого возможного подмножества признаков и нахождения того, который минимизирует величину ошибки. Это исчерпывающий поиск по пространству, и он является вычислительно трудным при большом количестве признаков. Выбор метрики влияет на выбор алгоритма. Метрики различаются для трёх основных категорий алгоритмов отбора признаков: обёртки, фильтры и методы вложения[3].
- Методы обёртывания используют модель априорной оценки результата для ранжирования поднаборов признаков. Каждый новый поднабор используется для обучения модели, которая проверяется на контрольной выборке. На этой контрольной выборке считается число ошибок (показатель ошибок модели), которое даёт оценку для данного подмножества. Так как методы обёртывания осуществляют перебор всех подмножеств признаков с последующем обучением модели, они наиболее вычислительно затратны, но дают, как правило, лучший набор признаков для конкретной модели.
- Методы фильтров используют косвенный показатель вместо показателя ошибки для оценки поднабора признаков. Этот показатель выбирается так, чтобы его можно было легко вычислить при сохранении показателя полезности набора признаков. Обычно применяемые меры — взаимная информация[3], поточечная взаимная информация[англ.][4], коэффициент корреляции смешанных моментов Пирсона, алгоритм, основанный на Relief[англ.][5] и расстояние между классами/внутри класса или результат критериев значимости для каждой комбинации класс/признак[4][6]. Фильтры обычно вычислительно менее интенсивны, чем обёртки, но они дают наборы признаков, которые не настроены на специфичный тип прогнозирующей модели[7]. Этот недостаток настройки означает, что набор признаков, полученный из фильтра, более общий, чем набор, полученный из обёртки, что приводит к меньшей обобщающей способности модели, чем у обёртки. Однако набор признаков не содержит предположений о прогнозирующей модели, а потому более пригоден для обнаружения связей между признаками. Многие фильтры обеспечивают ранжирование признаков, не давая явно лучшего их подмножества, а точка отсечения в ранжировании выбирается с помощью перекрёстной проверки. Методы фильтров используются также как предварительные шаги обработки для методов обёртывания, что позволяет применять обёртывание для больших задач. Другим популярным подходом является алгоритм рекурсивного исключения признаков, обычно используемый вместе с методом опорных векторов для многократного построения модели и удаления незначимых признаков.
- Методы вложения являются обобщающей группой техник, которые осуществляют отбор признаков как часть процесса построения модели. Примером такого подхода является метод LASSO[англ.] (англ. Least absolute shrinkage and selection operator — метод оценивания коэффициентов линейной регрессионной модели) для построения линейной модели, такой как -регуляризация, не давая коэффициентам модели расти и обнуляя наименее значимые. Любые признаки, которые имеют ненулевые коэффициенты регрессии, «выбираются» алгоритмом LASSO. Улучшения алгоритма LASSO включают алгоритм Bolasso, который формирует выборку путём бутстрэпа[8], регуляризации эластичной сети[англ.], которая комбинирует штраф алгоритма LASSO со штрафом гребневой регрессии, и метода FeaLect, который оценивает все признаки на основе комбинаторного анализа коэффициентов регрессии[9]. Эти подходы по вычислительной сложности оказываются где-то между фильтрами и обёртками.
В традиционной статистике наиболее популярной формой отбора признаков является ступенчатая регрессия[англ.], которая является техникой оборачивания. Это жадный алгоритм, который добавляет лучший признак (или удаляет худший) на каждом шаге алгоритма. Главная проблема — момент остановки алгоритма. При обучении моделей это обычно делается путём перекрёстной проверки. В статистике некоторые критерии оптимизированы. Это ведёт к наследованию проблемы вложения. Исследовались и более устойчивые методы, такие как метод ветвей и границ и кусочно-линейная сеть.
Выбор поднабора
Выбор поднабора оценивает поднабор признаков, как группу стабильности. Алгоритмы выбора поднабора можно разбить на «Обёртки», «Фильтры» и «Вложения». Обёртки используют алгоритм поиска для анализа пространства на возможные признаки и оценивают каждый поднабор путём прогона модели на поднаборе. Обёртки могут быть вычислительно затратны и имеют риск переобучения модели. «Фильтры» похожи на «Обёртки» по подходу к поиску, но вместо оценки модели ранжируется более простой фильтр. Техники «Вложения» встраиваются в модель и специфичны для неё.
Многие популярные подходы используют жадный поиск восхождением к вершине, который итеративно оценивает поднабор признаков как кандидата, затем модифицирует поднабор и оценивает, насколько новый поднабор лучше старого. Оценка поднабора требует использования оценочной метрики[англ.], которая ранжирует поднаборы признаков. Исчерпывающий поиск, как правило, невыполним, так что разработчик (или оператор) определяет точку остановки, и поднабор признаков с наибольшей достигнутой оценкой, обнаруженный к этому моменту, выбирается как удовлетворительный поднабор признаков. Критерий остановки зависит от алгоритма. Возможные критерии: оценка поднабора превышает порог, программа превысила максимальное допустимое время, и так далее.
Альтернативные техники на основе поиска базируются на целевом поиске наилучшей проекции[англ.], который находит проекции низкой размерности данных с высокой оценкой — выбираются признаки, которые имеют наибольшие проекции в пространстве низкой размерности.
Подходы для поиска:
- Исчерпывающий поиск
- Поиск по первому наилучшему совпадению
- Имитации отжига
- Генетический алгоритм[10]
- Жадный прямой отбор[11][12][13]
- Жадное обратное исключение
- Метод роя частиц[14]
- Целевой поиск наилучшей проекции[англ.]
- Распределенный поиск[15]
- Поиск с чередующимися окрестностями[англ.][16][17]
Две популярные метрики фильтров для задач классификации — корреляция и взаимная информация, хотя ни одна из них не является истинной метрикой[англ.] или «мерой расстояния» в математическом смысле, поскольку для них не выполняется неравенство треугольника, а потому они не представляют действительного «расстояния» — их следует, скорее, понимать как «оценку». Эти оценки вычисляются между признаками-кандидатами (или наборами признаков) и желаемой категорией. Есть, однако, истинные метрики, которые являются простыми функциями от взаимной информации[18].
Другие возможные метрики фильтров:
- Отделимость классов
- Вероятность ошибки
- Межклассовое расстояние
- Вероятностное расстояние
- Энтропия
- Выбор признаков на основе непротиворечивости
- Выбор признаков на основе корреляции.
Критерий оптимальности
Выбор критерия оптимальности сложен, так как имеется несколько целей в задаче отбора признаков. Многие критерии включают меру точности со штрафованием числом выбранных признаков (например, байесовский информационный критерий). Наиболее старыми являются статистика Cp Мэллоуса[англ.] и информационный критерий Акаике (англ. Akaike information criterion, AIC). Они добавляют переменные, если t-статистика превосходит .
Другими критериями являются байесовский информационный критерий (БИК, англ. Bayesian information criterion, BIC), который использует , минимальная длина описания (англ. minimum description length, MDL), который асимптотически использует , Бонферрони / RIC, который использует , отбор признаков с максимальной зависимостью, и набор новых критериев, которые продиктованы идеей уровня ложноположительных результатов[англ.] (англ. false discovery rate, FDR) и которые используют нечто, близкое к . Критерий максимума энтропийной скорости может также быть использован для выбора наиболее значимого поднабора признаков[19].
Структурное обучение
Фильтр отбора признаков является специальным случаем более общей парадигмы с названием «структурное обучение». Выбор признаков находит значимый набор признаков для конкретной целевой переменной, в то время как структурное обучение находит связи между переменными, обычно выражая эти связи в виде графа. Наиболее распространённые алгоритмы структурного обучения предполагают, что данные генерируются байесовской сетью, так что структура является ориентированной графовой моделью. Оптимальное решение задачи фильтра отбора признаков является марковским ограждением целевого узла и в байесовской сети имеется единственное марковское ограждение для каждого узла[20].
Механизмы отбора признаков на основе информационной теории
Есть различные механизмы отбора признаков, которые используют взаимную информацию для оценки различных признаков. Они обычно используют один и тот же алгоритм:
- Вычисляется взаимная информация как оценка между всеми признаками () и целевым классом ()
- Выбирается признак с наибольшей оценкой (например, ) и добавляется в набор отобранных признаков ()
- Вычисляется оценка, которая может быть получена из взаимной информации
- Выбираем признак с наибольшей оценкой и добавляем в набор отобранных признаков (например, )
- Повторяем шаги 3. и 4. Пока не наберём определённое число признаков (например, )
Наиболее простой подход использует взаимную информацию в качестве «производной» оценки[21].
Однако, есть различные походы, которые пытаются уменьшить избыточность между признаками.
Выбор признаков на основе минимальной избыточности-максимальной релевантности
Пэн, Лон и Дин[22] предложили метод отбора признаков, который может использовать взаимную информацию, корреляцию или оценку расстояния/похожести для отбора признаков. Целью является наложение штрафа на значимость признака при избыточности, вызванной присутствием в других выбранных признаках. Значимость набора признаков S для класса c определяется средним значением всех значений взаимной информации между индивидуальным признаком fi и классом c:
Избыточность всех признаков в наборе S равна среднему значению всех значений взаимной информации между признаком fi и признаком fj:
Критерий минимальной избыточности-максимальной релевантности (англ. Minimum-redundancy-maximum-relevance, mRMR) является комбинацией двух мер, заданных выше и определённой как:
Предположим, что имеется полный набор из n признаков. Пусть xi будет индикаторной функцией вхождения в множество fi, так что xi=1 отражает присутствие, а xi=0 отражает отсутствие признака fi в глобальном оптимальном наборе признаков. Пусть и . Формула выше может теперь быть переписана как задача оптимизации:
Алгоритм mRMR является аппроксимацией теоретически оптимального алгоритма отбора признаков с максимальной зависимостью, который максимизирует взаимную информацию между совместным распределением выбранных признаков и классификационной переменной. Так как mRMR аппроксимирует задачу комбинаторной оценки серией существенно меньших задач, каждая из которых использует только две переменные, он использует попарные совместные вероятности, которые более устойчивы. В некоторых ситуациях алгоритм может недооценить полезность признаков, так как он не имеет возможности измерить взаимосвязь между признаками, которая может увеличить значимость. Это может привести к плохой производительности[21], если признаки по отдельности бесполезны, но становятся значимыми в комбинации (патологический случай найден, когда класс является функцией чётности[англ.] признаков). В общем случае алгоритм более эффективен (в терминах количества требуемых данных), чем теоретически оптимальный выбор максимальной зависимости, всё же даёт набор признаков с небольшой попарной избыточностью.
Алгоритм mRMR является представителем большого класса методов фильтров, которые балансируют различным образом между значимостью и избыточностью[21][23].
Квадратичное программирование для отбора признаков
Алгоритм mRMR является типичным примером инкрементальной жадной стратегии для отбора признаков — как только признак выбран, он не может быть удалён из выборки на последующих шагах. В то время как mRMR можно оптимизировать с помощью плавающего поиска для сокращения некоторых признаков, его можно переформулировать как глобальную оптимизационную задачу квадратичного программирования[24]:
- ,
где является вектором значимости признаков в предположении, что имеется всего n признаков, является матрицей попарной значимости, а представляет относительные веса признаков. Задача QPFS решается методами квадратичного программирования. Было показано, что QFPS смещена в направлении признаков с меньшей энтропией[25] вследствие самоизбыточности признака на диагонали матрицы H.
Условная взаимная информация
Другая оценка, производная от взаимной информации, основана на условной значимости[25]:
где и .
Преимущество SPECCMI заключается в том, что оно может быть решено просто путём нахождения доминирующего собственного вектора Q. SPECCMI обрабатывает также для признаков взаимосвязи второго порядка.
Совместная взаимная информация
При изучении различных оценок Браун, Поукок, Чжао и Лухан[21] рекомендовали совместную взаимную информацию[26] в качестве хорошей оценки для отбора признаков. Оценка пытается найти признак, который добавляет наибольшую новую информацию к уже отобранным признакам, чтобы избежать избыточность. Оценка формулируется следующим образом:
Оценка использует условную взаимную информацию и взаимную информацию для оценки избыточности между уже отобранными признаками () и исследуемым признаком ().
Выбор признаков на основе критерия независимости Lasso Гильберта — Шмидта
Для данных высокой размерности и небольших данных (например, размерность > и размер выборки < ), полезным является критерий независимости Lasso Гильберта — Шмидта (HSIC Lasso)[27]. Задача оптимизации HSIC Lasso задаётся как
- ,
где является ядерной мерой независимости, называемой (эмпирическим) критерием независимости Гильберта — Шмидта (англ. Hilbert-Schmidt independence criterion, HSIC), обозначает след, является параметром регуляризации, и являются входными и выходными центрированными матрицами Грама, и являются матрицами Грама, и являются ядерными функциями, является центрированной матрицей, является m-мерной единичной матрицей (m: число элементов выборки), является m-мерным вектором со всеми единицами, а является -нормой. HSIC всегда принимает неотрицательное значение и равно нулю тогда и только тогда, когда две случайные переменные статистически независимы при применении универсального производящего ядра, такого как гауссово ядро.
HSIC Lasso можно записать как:
- ,
где является нормой Фробениуса. Задача оптимизации является задачей Lasso, а потому она может быть эффективно решена с помощью современных методов решения Lasso, таких как двойственный метод обобщённого Лагранжиана[англ.].
Отбор признаков на основе корреляции
Отбор признаков на основе меры корреляции (англ. Correlation Feature Selection, CFS) оценивает подмножества признаков на базе следующей гипотезы: «Хорошие поднаборы признаков содержат признаки, сильно коррелирующие с классификацией, но не коррелирующие друг с другом»[28][29]. Следующее равенство даёт оценку поднабора признаков S, состоящего из k признаков:
Здесь является средним значением всех корреляций признак-классификация, а является средним всех корреляций признак-признак. Критерий CFS определяется следующим образом:
Переменные и являются корреляциями, но не обязательно коэффициентами корреляции Пирсона или ρ Спирмена[англ.]*. Диссертация Марка Холла не использует ни одну из них, но использует три различных меры связанности, минимальную длину описания (англ. minimum description length, MDL), симметричную неопределённость и Relief[англ.].
Пусть xi будет индикаторной функцией вхождения в множество для признака fi. Тогда формула выше может быть переписана как задача оптимизации:
Комбинаторные задачи выше являются, фактически, смешанными 0-1 задачами линейного программирования, которые могут быть решены с помощью алгоритма ветвей и границ[30].
Регуляризованные деревья
Было показано, что признаки из дерева решений или ансамбли деревьев избыточны. Недавний метод с названием «регуляризованное дерево»[31] может быть использован для выбора поднабора признаков. Регуляризованные деревья штрафуются с помощью переменной, подобной переменным, выбранным на предыдущих узлах дерева для расщепления текущего узла. Для регуляризованных деревьев нужно строить только одну модель (иди один ансамбль деревьев), а потому вычислительно алгоритм эффективен.
Регуляризованные деревья естественным образом работают с численными и категорийными признаками, взаимодействиями и нелинейностями. Они инвариантны относительно масштаба атрибутов (единиц) и нечувствительны к выбросам, а потому требуют малой предварительной обработки данных, такой как нормализация[англ.]. Регуляризованный случайный лес (англ. Regularized random forest, RRF)[32] является одним из типов регуляризованных деревьев. Управляемый RRF является улучшенным методом RRF, который управляется оценкой важности из обычного случайного леса.
Обзор методов метаэвристики
Метаалгоритм (или метаэвристика) является общим описанием алгоритма, предназначенного для решения трудных (типично, NP-трудных задач) задач оптимизации для которых не имеется никаких методов решения. Обычно метаалгоритм является стохастическим алгоритмом, стремящимся достичь глобального оптимума. Есть много метаалгоритмов от простого локального поиска до сложного алгоритма глобального поиска.
Основные принципы
Методика отбора признаков обычно представлены тремя классами по тому, как они комбинируют алгоритмы выбора и построения модели.
Метод фильтров

Методы фильтров выбирают переменные независимо от модели. Они базируются только на общих признаках, таких как корреляция переменной с предсказанием. Методы фильтров подавляют наименее интересные переменные. Другие переменные будут частью классификации или модели регрессии, использованной для классификации или предсказания. Эти методы очень эффективны по времени вычисления и устойчивы к переобучению[33].
Однако, методы фильтров стремятся к выбору избыточных переменных, поскольку они не учитывают связь между переменными. По этой причине эти методы главным образом используются как методы предварительной обработки.
Метод обёртывания
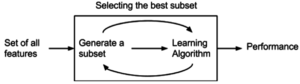
Методы обёртывания оценивают поднаборы переменных и позволяют, в отличие от подходов фильтрации, обнаружить возможную взаимосвязь между переменными[34]. Два главных недостатка этих методов:
- Увеличивается риск переобучения, когда число наблюдений недостаточно.
- Существенное время вычисления, когда число переменных велико.
Метод вложения
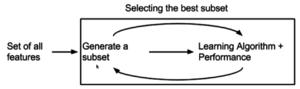
Методы вложения были предложены как попытка комбинации преимуществ двух предыдущих методов. Обучающий алгоритм имеет преимущество собственного процесса выбора переменной и осуществляет выбор признаков и классификацию одновременно.
Приложение метаэвристики отбора признаков
Ниже обзор приложений метаалгоритмов отбора признаков, использованных в литературе. Обзор был приведён в тезисах Джулии Хэммон[33].
| Приложение | Алгоритм | Подход | классификатор | Ценностная функция[англ.] | Ссылка |
|---|---|---|---|---|---|
| ОНП | Выбор признаков с помощью похожести признаков | Фильтр | r2 | Фыонг 2005[34] | |
| ОНП | Генетический алгоритм | Обёртка | Decision Tree | Правильность классификации (10-кр) | Шах, Кусиак 2004[35] |
| ОНП | Поиск восхождением к вершине | Фильтр + Обёртка | Наивный байесовский классификатор | Предсказочная остаточная суммаквадртаов | Лон 2007[36] |
| ОНП | Алгоритм имитации отжига | Наивный байесовский классификатор | Правильность классификации (5-кр) | Устункар 2011[37] | |
| Segments parole | Алгоритм муравьиной колонии | Обёртка | Искусственная нейронная сеть | MSE[англ.] | Аль-ани 2005 |
| Marketing | Алгоритм имитации отжига | Обёртка | Регрессия | AIC, r2 | Мейри 2006[38] |
| Economy | Алгоритм имитации отжига, Генетический алгоритм | Обёртка | Регрессия | БИК | Капетаниос 2005[39] |
| Spectral Mass | Генетический алгоритм | Обёртка | Множественная линейная регрессич, Частные наименьшие квадраты[англ.] | Среднеквадратичная ошибка[англ.] предсказания | Бродхёрст 2007[40] |
| Spam | Бинарный метод роя частиц + Мутация[англ.] | Обёртка | Дерево решений | взвешенная цена | Джанг 2014[14] |
| Микроматрица | Поиск с запретами + Метод роя частиц | Обёртка | Метод опорных векторов, Метод k ближайших соседей | Евклидова метрика | Чанг, Янг 2009[41] |
| Микроматрица | PSO + Генетический алгоритм | Обёртка | Метод опорных векторов | Правильность классификации (10-кр) | Альба 2007[42] |
| Микроматрица | Генетический алгоритм + Итеративный локальный поиск[англ.] | Вложенный | Метод опорных векторов | Правильность классификации (10-кр) | Дювал 2009[43] |
| Микроматрица | Обёртка | Регрессия | Апостериорная вероятность | Ханс, Дорба, Вест 2007[44] | |
| Микроматрица | Генетический алгоритм | Обёртка | Метод k ближайших соседей | Правильность классификации (Перекрёстная проверка с исключением) | Эйткен 2005[45] |
| Микроматрица | Гибридный генетический алгоритм[англ.] | Обёртка | Метод k ближайших соседей | Правильность классификации (перекрёстная проверка с исключением) | Ох, Мун 2004[46] |
| Микроматрица | Генетический алгоритм | Обёртка | Метод опорных векторов | Чувствительность и специфичность | Сюань 2011[47] |
| Микроматрица | Генетический алгоритм | Обёртка | Попарный метод опорных векторов | Правильность классификации (перекрёстная проверка с исключением) | Пэн 2003[48] |
| Микроматрица | Генетический алгоритм | Вложенный | Метод опорных векторов | Правильность классификации (10-кр) | Эрнандес 2007[49] |
| Микроматрица | Генетический алгоритм | Hybrid | Метод опорных векторов | Правильность классификации (перекрёстная проверка с исключением) | Уэрта 2006[50] |
| Микроматрица | Генетический алгоритм | Метод опорных векторов | Правильность классификации (10-кр) | Муни, Пал, Дас 2006[51]. | |
| Микроматрица | Генетический алгоритм | Обёртка | Метод опорных векторов | EH-DIALL, CLUMP | Журден 2011[52]. |
| Болезнь Альцгеймера | t-тест Уэлча[англ.]* | Фильтр | ядерный метод опорных векторов | Правильность классификации (10-кр) | Чжан 2015[53] |
| Компьютерное зрение | Бесконечный отбор признаков | Фильтр | Независим | Средняя точность[англ.], ROC-площадь под кривой | Роффо 2015[54] |
| Микроматрицы | Eigenvector Centrality FS | Фильтр | Независим | Средняя точность, Точность, ROC AUC | Роффо, Мельци 2016[55] |
| XML | Симметричный Тау-алгоритм | Фильтр | Структурная ассоциативная классификация | Точность, Покрытие | Шахарани, Хаджич 2014 |
Выбор признаков, вложенных в алгоритмы обучения
Некоторые обучающие алгоритмы осуществляют отбор признаков как часть алгоритма:
- Техники -регуляризации, такие как разреженная регрессия, LASSO, и -SVM
- Регуляризованные деревья[31], например, регуляризованный случайный лес, реализованный в пакете RRF[32]
- Дерево решений[56]
- Меметический алгоритм[англ.]
- Случайный мультиномиальный логит (англ. Random multinomial logit, RMNL)
- Автокодирующая сеть с узким уровнем
- Выделение субмодулярных[англ.] признаков[57][58][59]
- Выбор признаков на основе локального обучения[60]. По сравнению с традиционными методами данный метод не использует эвристического поиска, может легко справляться с задачами с большим количеством классов, и работает как на линейных, так и нелинейных задачах. Метод также поддержан с теоретической стороны. Численные эксперименты показали, что метод может достичь близкое к оптимальному решение даже в случае, когда данные содержат более миллиона незначимых признаков.
См. также
- Кластерный анализ
- Data mining
- Снижение размерности
- Выделение признаков
- Оптимизация гиперпараметров
- Алгоритм Relief[англ.]
Примечания
- ↑ James, Witten, Hastie, Tibshirani, 2013, с. 204.
- ↑ 1 2 Bermingham, Pong-Wong, Spiliopoulou и др., 2015, с. 10312.
- ↑ 1 2 3 Guyon, Elisseeff, 2003.
- ↑ 1 2 Yang, Pedersen, 1997.
- ↑ Urbanowicz, Meeker, LaCava, Olson, Moore, 2017.
- ↑ Forman, 2003, с. 1289–1305.
- ↑ Zhang, Li, Wang, Zhang, 2013, с. 32–42.
- ↑ Bach, 2008, с. 33–40.
- ↑ Zare, 2013, с. S14.
- ↑ Soufan, Kleftogiannis, Kalnis, Bajic, 2015, с. e0117988.
- ↑ Figueroa, 2015, с. 162–169.
- ↑ Figueroa, Neumann, 2013.
- ↑ Figueroa, Neumann, 2014, с. 4730–4742.
- ↑ 1 2 Zhang, Wang, Phillips, 2014, с. 22–31.
- ↑ Garcia-Lopez, Garcia-Torres, Melian, Moreno-Perez, Moreno-Vega, 2006, с. 477–489.
- ↑ Garcia-Lopez, Garcia-Torres, Melian, Moreno-Perez, Moreno-Vega, 2004, с. 59–68.
- ↑ Garcia-Torres, Gomez-Vela, Melian, Moreno-Vega, 2016, с. 102—118.
- ↑ Kraskov, Stögbauer, Andrzejak, Grassberger, 2003.
- ↑ Einicke, 2018, с. 1097–1103.
- ↑ Aliferis, 2010, с. 171–234.
- ↑ 1 2 3 4 Brown, Pocock, Zhao, Luján, 2012, с. 27—66.
- ↑ Peng, Long, Ding, 2005, с. 1226–1238.
- ↑ Nguyen, Franke, Petrovic, 2010, с. 1529—1532.
- ↑ Rodriguez-Lujan, Huerta, Elkan, Santa Cruz, 2010, с. 1491–1516.
- ↑ 1 2 Vinh, Chan, Romano, Bailey, 2014.
- ↑ Yang, Moody, 2000, с. 687—693.
- ↑ Yamada, Jitkrittum, Sigal, Xing, Sugiyama, 2014, с. 185—207.
- ↑ Hall, 1999.
- ↑ Senliol, Gulgezen, Yu, Cataltepe, 2008, с. 1—4.
- ↑ Nguyen, Franke, Petrovic, 2009.
- ↑ 1 2 Deng, Runger, 2012.
- ↑ 1 2 RRF: Regularized Random Forest Архивная копия от 5 января 2019 на Wayback Machine, пакет на языке R в репозитории Comprehensive R Archive Network (CRAN)
- ↑ 1 2 Hammon, 2013.
- ↑ 1 2 Phuong, Lin, Altman, 2005, с. 301—309.
- ↑ Shah, Kusiak, 2004, с. 183–196.
- ↑ Long, Gianola, Weigel, 2011, с. 247–257.
- ↑ Ustunkar, Ozogur-Akyuz, Weber, Friedrich, Son, 2011, с. 1207–1218.
- ↑ Meiri, Zahavi, 2006, с. 842—858.
- ↑ Kapetanios, 2005.
- ↑ Broadhurst, Goodacre, Jones, Rowland, Kell, 1997, с. 71—86.
- ↑ Chuang, Yang, 2009, с. 1689–1703.
- ↑ Alba, Garia-Nieto, Jourdan, Talbi, 2007.
- ↑ Duval, Hao, Hernandez, 2009, с. 201—208.
- ↑ Hans, Dobra, West, 2007, с. 507—516.
- ↑ Aitken, 2005, с. 148.
- ↑ Oh, Moon, 2004, с. 1424–1437.
- ↑ Xuan, Guo, Wang, Liu, Liu, 2011, с. 588–603.
- ↑ Peng, 2003, с. 358–362.
- ↑ Hernandez, Duval, Hao, 2007, с. 90—101.
- ↑ Huerta, Duval, Hao, 2006, с. 34—44.
- ↑ Muni, Pal, Das, 2006, с. 106—117.
- ↑ Jourdan, Dhaenens, Talbi, 2011.
- ↑ Zhang, Dong, Phillips, Wang, 2015, с. 66.
- ↑ Roffo, Melzi, Cristani, 2015, с. 4202–4210.
- ↑ Roffo, Melzi, 2016, с. 19—38.
- ↑ Kohavi, John, 1997, с. 273—324.
- ↑ Das, Kempe, 2011.
- ↑ Liu, Wei, Kirchhoff, Song, Bilmes, 2013.
- ↑ Zheng, Jiang, Chellappa, Phillip, 2014.
- ↑ Sun, Todorovic, Goodison, 2010, с. 1610—1626.
Литература
- Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. An Introduction to Statistical Learning. — Springer, 2013.
- Mairead L. Bermingham, Ricardo Pong-Wong, Athina Spiliopoulou, Caroline Hayward, Igor Rudan, Harry Campbell, Alan F. Wright, James F. Wilson, Felix Agakov, Pau Navarro, Chris S. Haley. Application of high-dimensional feature selection: evaluation for genomic prediction in man // Sci. Rep.. — 2015. — Т. 5. — doi:10.1038/srep10312. — . — PMID 25988841. — PMC 4437376.
- Othman Soufan, Dimitrios Kleftogiannis, Panos Kalnis, Vladimir B. Bajic. DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm // PLOS One. — 2015. — Т. 10, вып. 2. — ISSN 1932-6203. — doi:10.1371/journal.pone.0117988. — . — PMID 25719748. — PMC 4342225.
- Alejandro Figueroa. Exploring effective features for recognizing the user intent behind web queries // Computers in Industry. — 2015. — Т. 68. — doi:10.1016/j.compind.2015.01.005.
- Alejandro Figueroa, Guenter Neumann. Learning to Rank Effective Paraphrases from Query Logs for Community Question Answering // 27th AAAI Conference on Artificial Intelligence. — 2013.
- Alejandro Figueroa, Guenter Neumann. Category-specific models for ranking effective paraphrases in community Question Answering // Expert Systems with Applications. — 2014. — Т. 41, вып. 10. — doi:10.1016/j.eswa.2014.02.004.
- Zhang Y., Wang S., Phillips P. Binary PSO with Mutation Operator for Feature Selection using Decision Tree applied to Spam Detection // Knowledge-Based Systems. — 2014. — Т. 64. — doi:10.1016/j.knosys.2014.03.015.
- Garcia-Lopez F.C., Garcia-Torres M., Melian B., Moreno-Perez J.A., Moreno-Vega J.M. Solving feature subset selection problem by a Parallel Scatter Search // European Journal of Operational Research. — 2006. — Т. 169, № 2.
- Garcia-Lopez F.C., Garcia-Torres M., Melian B., Moreno-Perez J.A., Moreno-Vega J.M. Solving Feature Subset Selection Problem by a Hybrid Metaheuristic // First International Workshop on Hybrid Metaheuristics. — 2004. — С. 59–68.
- Garcia-Torres M., Gomez-Vela F., Melian B., Moreno-Vega J.M. High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach // Information Sciences. — 2016. — Т. 326.
- Alexander Kraskov, Harald Stögbauer, Ralph G. Andrzejak, Peter Grassberger. Hierarchical Clustering Based on Mutual Information. — 2003. — . — arXiv:q-bio/0311039.
- Nguyen X. Vinh, Jeffrey Chan, Simone Romano, James Bailey. Effective Global Approaches for Mutual Information based Feature Selection // 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD'14), August 24–27. — New York City, 2014.
- Howard Hua Yang, John Moody. Data visualization and feature selection: New algorithms for nongaussian data // Advances in Neural Information Processing Systems. — 2000.
- Yamada M., Jitkrittum W., Sigal L., Xing E. P., Sugiyama M. High-Dimensional Feature Selection by Feature-Wise Non-Linear Lasso // Neural Computation. — 2014. — Т. 26, № 1.
- Mark A. Hall. Correlation-based Feature Selection for Machine Learning. — 1999.
- Baris Senliol, Gokhan Gulgezen, Lei Yu, Zehra Cataltepe. Fast Correlation Based Filter (FCBF) with a different search strategy // ISCIS'08. 23rd International Symposium on.. — IEEE, 2008. — С. 1—4.
- Hai Nguyen, Katrin Franke, Slobodan Petrovic. Optimizing a class of feature selection measures // Conference NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML), Vancouver, Canada, December 2009. — 2009.
- Hammon J. Optimisation combinatoire pour la sélection de variables en régression en grande dimension : Application en génétique animale.. — 2013.
- Kohavi R., John G. Wrappers for feature subset selection // Artificial intelligence 97. — 1997. — Вып. 1—2.
- Deng H., Runger G. Feature Selection via Regularized Trees // Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN). — IEEE, 2012.
- Phuong T. M., Lin Z., Altman R. B. Choosing SNPs using feature selection // IEEE Computational Systems Bioinformatics Conference, CSB. IEEE Computational Systems Bioinformatics Conference. — 2005. Архивная копия от 13 сентября 2016 на Wayback Machine
- Gavin Brown, Adam Pocock, Ming-Jie Zhao, Mikel Luján. Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection // Journal of Machine Learning Research. — 2012. — Т. 13. [1]
- Shah S. C., Kusiak A. Data mining and genetic algorithm based gene/SNP selection // Artificial Intelligence in Medicine. — 2004. — Т. 31, вып. 3. — doi:10.1016/j.artmed.2004.04.002. — PMID 15302085.
- Long N., Gianola D., Weigel K. A. Dimension reduction and variable selection for genomic selection: application to predicting milk yield in Holsteins // Journal of Animal Breeding and Genetics. — 2011. — Т. 128, вып. 4. — doi:10.1111/j.1439-0388.2011.00917.x. — PMID 21749471.
- Ustunkar G., Ozogur-Akyuz S., Weber G. W., Friedrich C. M., Yesim Aydin Son. Selection of representative SNP sets for genome-wide association studies : a metaheuristic approach // Optimization Letters. — Springer-Verlag, 2011. — Ноябрь (т. 6, вып. 6). — doi:10.1007/s11590-011-0419-7.
- Meiri R., Zahavi J. Using simulated annealing to optimize the feature selection problem in marketing applications // European Journal of Operational Research. — 2006. — Juin (т. 171, № 3).
- Kapetanios G. Variable Selection using Non-Standard Optimisation of Information Criteria. — 2005. — (Working Paper, Queen Mary, University of London, School of Economics and Finance).
- Broadhurst D., Goodacre R., Jones A., Rowland J. J., Kell D. B. Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry // Analytica Chimica Acta. — 1997. — Август (т. 348, № 1—3).
- Chuang L.-Y., Yang C.-H. Tabu search and binary particle swarm optimization for feature selection using microarray data // Journal of Computational Biology. — 2009. — Т. 16, вып. 12. — doi:10.1089/cmb.2007.0211. — PMID 20047491.
- Alba E., Garia-Nieto J., Jourdan L., Talbi E.-G. Gene Selection in Cancer Classification using PSO-SVM and GA-SVM Hybrid Algorithms // Congress on Evolutionary Computation, Singapor, 2007. — Singapore, 2007.
- Duval B., Hao J.-K., Hernandez J. C. H. A memetic algorithm for gene selection and molecular classification of an cancer // Proceedings of the 11th Annual conference on Genetic and evolutionary computation, GECCO '09. — New York, NY, USA: ACM, 2009.
- Hans C., Dobra A., West M. Shotgun stochastic search for 'large p' regression // Journal of the American Statistical Association. — 2007. — Т. 102, вып. 478. — С. 507—516. — ISSN 0162-1459. — doi:10.1198/016214507000000121.
- Isabelle Guyon, André Elisseeff. An Introduction to Variable and Feature Selection // JMLR. — 2003. — Т. 3.
- Ryan J. Urbanowicz, Melissa Meeker, William LaCava, Randal S. Olson, Jason H. Moore. Relief-Based Feature Selection: Introduction and Review // Journal of Biomedical Informatics. — 2017. — Вып. 85. — doi:10.1016/j.jbi.2018.07.014.
- Yiming Yang, Jan O. Pedersen. A comparative study on feature selection in text categorization // Proceedings of the Fourteenth International Conference on Machine Learning (ICML). — 1997. — ISBN 1-55860-486-3.
- George Forman. An extensive empirical study of feature selection metrics for text classification // Journal of Machine Learning Research. — 2003. — Т. 3. — ISSN 1533-7928.
- Yishi Zhang, Shujuan Li, Teng Wang, Zigang Zhang. Divergence-based feature selection for separate classes // Neurocomputing. — 2013. — Т. 101, вып. 4. — doi:10.1016/j.neucom.2012.06.036.
- Francis R. Bach. Bolasso: model consistent lasso estimation through the bootstrap. — Proceedings of the 25th International Conference on Machine Learning. — 2008. — ISBN 9781605582054. — doi:10.1145/1390156.1390161.
- Habil Zare. Scoring relevancy of features based on combinatorial analysis of Lasso with application to lymphoma diagnosis // BMC Genomics. — 2013. — Т. 14. — doi:10.1186/1471-2164-14-S1-S14. — PMID 23369194. — PMC 3549810.
- Einicke G. A. Maximum-Entropy Rate Selection of Features for Classifying Changes in Knee and Ankle Dynamics During Running // IEEE Journal of Biomedical and Health Informatics. — 2018. — Т. 28, вып. 4. — doi:10.1109/JBHI.2017.2711487. — PMID 29969403.
- Constantin Aliferis. Local causal and markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation // Journal of Machine Learning Research. — 2010. — Т. 11.
- Peng H. C., Long F., Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 2005. — Т. 27, вып. 8. — doi:10.1109/TPAMI.2005.159. — PMID 16119262. Программа
- Nguyen H., Franke K., Petrovic S. Towards a Generic Feature-Selection Measure for Intrusion Detection // 20h International Conference on Pattern Recognition (ICPR). — Istanbul, Turkey, 2010.
- Rodriguez-Lujan I., Huerta R., Elkan C., Santa Cruz C. Quadratic programming feature selection // JMLR. — 2010. — Т. 11.
- Aitken S. Feature selection and classification for microarray data analysis : Evolutionary methods for identifying predictive genes // BMC Bioinformatics. — 2005. — Т. 6, вып. 1. — doi:10.1186/1471-2105-6-148. — PMID 15958165. — PMC 1181625.
- Oh I. S., Moon B. R. Hybrid genetic algorithms for feature selection // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 2004. — Т. 26, вып. 11. — doi:10.1109/tpami.2004.105. — PMID 15521491.
- Xuan P., Guo M. Z., Wang J., Liu X. Y., Liu Y. Genetic algorithm-based efficient feature selection for classification of pre-miRNAs // Genetics and Molecular Research. — 2011. — Т. 10, вып. 2. — doi:10.4238/vol10-2gmr969. — PMID 21491369.
- Peng S. Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines // FEBS Letters. — 2003. — Т. 555, вып. 2. — doi:10.1016/s0014-5793(03)01275-4.
- Jose Crispin Hernandez Hernandez, B´eatrice Duval, Jin-Kao Hao. A genetic embedded approach for gene selection and classification of microarray data // Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics, EvoBIO'07. — Berlin, Heidelberg: SpringerVerlag, 2007. — Т. 4447. — (Lecture Notes in Computer Science). — ISBN 3-540-71782-X.
- Huerta E. B., Duval B., Hao J.-K. A hybrid GA/SVM approach for gene selection and classification of microarray data. Evoworkshops // Applicationsof EvolutionaryComputing. — 2006. — Т. 3907. — С. 34—44. — (Lecture Notes in Computer Science).
- Muni D. P., Pal N. R., Das J. Genetic programming for simultaneous feature selection and classifier design // IEEE Transactions on Systems, Man, and Cybernetics, Part B : Cybernetics. — 2006. — Т. 36.
- Laetitia Jourdan, Clarisse Dhaenens, El-Ghazali Talbi. Linkage disequilibrium study with a parallel adaptive GA // International Journal of Foundations of Computer Science. — 2011. — Т. 16, вып. 2.
- Zhang Y., Dong Z., Phillips P., Wang S. Detection of subjects and brain regions related to Alzheimer's disease using 3D MRI scans based on eigenbrain and machine learning // Frontiers in Computational Neuroscience. — 2015. — Т. 9. — doi:10.3389/fncom.2015.00066. — PMID 26082713. — PMC 4451357.
- Roffo G., Melzi S., Cristani M. Infinite Feature Selection. — 2015 IEEE International Conference on Computer Vision (ICCV). — 2015. — ISBN 978-1-4673-8391-2. — doi:10.1109/ICCV.2015.478.
- Giorgio Roffo, Simone Melzi. Features Selection via Eigenvector Centrality // New Frontiers in Mining Complex Patterns, (NFMCP 2016).. — Springer, 2016. — Т. 10312. — С. 19—38. — (Lecture Notes in Artificial Intelligence (LNAI}). — ISBN 978-3-319-61460-1. — doi:10.1007/978-3-319-61461-8. Ссылка указывает на чуть отличающуюся версию статьи
- Abhimanyu Das, David Kempe. Submodular meets Spectral: Greedy Algorithms for Subset Selection, Sparse Approximation and Dictionary Selection // The 28th International Conference on Machine Learning. — 2011.
- Yuzong Liu, Kai Wei, Katrin Kirchhoff, Yisong Song, Jeff A. Bilmes. Submodular feature selection for high-dimensional acoustic score spaces // 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. — 2013. — doi:10.1109/ICASSP.2013.6639057.
- Jinging Zheng, Zhuolin Jiang, Rama Chellappa, P. Jonathon Phillip. Submodular Attribute Selection for Action Recognition in Video // Advances in Neural Information Processing Systems 27 (NIPS 2014) / Z. Ghahramani, M. Welling, C. Cortes, N.D. Lawrence, K.Q. Weinberger.. — 2014.
- Sun Y., Todorovic S., Goodison S. Local-Learning-Based Feature Selection for High-Dimensional Data Analysis] // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 2010. — Т. 32.
- Feature Selection for Classification: A Review (Survey, 2014)
- Feature Selection for Clustering: A Review (Survey, 2013)
- Tutorial Outlining Feature Selection Algorithms, Arizona State University
- JMLR Special Issue on Variable and Feature Selection
- Feature Selection for Knowledge Discovery and Data Mining (Book)
- An Introduction to Variable and Feature Selection (Survey)
- Toward integrating feature selection algorithms for classification and clustering (Survey)
- Efficient Feature Subset Selection and Subset Size Optimization (Survey, 2010)
- Searching for Interacting Features
- Feature Subset Selection Bias for Classification Learning
Ссылки
- Feature Selection Package, Arizona State University (Matlab Code)
- NIPS challenge 2003 (see also NIPS)
- Naive Bayes implementation with feature selection in Visual Basic Архивная копия от 14 февраля 2009 на Wayback Machine (includes executable and source code)
- Minimum-redundancy-maximum-relevance (mRMR) feature selection program
- FEAST (Open source Feature Selection algorithms in C and MATLAB)














![{\displaystyle \mathrm {mRMR} =\max _{S}\left[{\frac {1}{|S|}}\sum _{f_{i}\in S}I(f_{i};c)-{\frac {1}{|S|^{2}}}\sum _{f_{i},f_{j}\in S}I(f_{i};f_{j})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eec7b98cd9e6fc9b3b61c0ac4712a16379c8859)


![{\displaystyle \mathrm {mRMR} =\max _{x\in \{0,1\}^{n}}\left[{\frac {\sum _{i=1}^{n}c_{i}x_{i}}{\sum _{i=1}^{n}x_{i}}}-{\frac {\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j}}{(\sum _{i=1}^{n}x_{i})^{2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0baef01e8c550ba917099a82e0ac43e826f59d37)

![{\displaystyle F_{n\times 1}=[I(f_{1};c),\ldots ,I(f_{n};c)]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e655a9d669fdf3ca7c6572563f8b5d1c1d7af44e)
![{\displaystyle H_{n\times n}=[I(f_{i};f_{j})]_{i,j=1\ldots n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5d1966a8fa8bd4894b5d768dcfc4da9b1caa9de)





![{\displaystyle {\begin{aligned}JMI(f_{i})&=\sum _{f_{j}\in S}(I(f_{i};c)+I(f_{i};c|f_{j}))\\&=\sum _{f_{j}\in S}{\bigl [}I(f_{j};c)+I(f_{i};c)-{\bigl (}I(f_{i};f_{j})-I(f_{i};f_{j}|c){\bigr )}{\bigr ]}\end{aligned}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8eb2ceaf7a6af44b2ffa159591b4ea6a6c44743)
























![{\displaystyle \mathrm {CFS} =\max _{S_{k}}\left[{\frac {r_{cf_{1}}+r_{cf_{2}}+\cdots +r_{cf_{k}}}{\sqrt {k+2(r_{f_{1}f_{2}}+\cdots +r_{f_{i}f_{j}}+\cdots +r_{f_{k}f_{1}})}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dfb56cea66ca7f2e039615b8c586ed355caf9e9)


![{\displaystyle \mathrm {CFS} =\max _{x\in \{0,1\}^{n}}\left[{\frac {(\sum _{i=1}^{n}a_{i}x_{i})^{2}}{\sum _{i=1}^{n}x_{i}+\sum _{i\neq j}2b_{ij}x_{i}x_{j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9491bc46548bd4416952e59704e78388e8726480)