Отношение шансов

Отношение шансов — характеристика, применяемая в математической статистике (на русском обозначается аббревиатурой «ОШ», на английском «OR» от odds ratio) для количественного описания тесноты связи признака А с признаком Б в некоторой статистической популяции.

Рассмотрим принцип вычисления этого показателя на гипотетическом примере. Предположим, что нескольким добровольцам задают два вопроса:

1. Каково ваше артериальное давление?
2. Сколько алкоголя вы употребляете?

Далее, для каждого участника можно определить обладает ли он свойством «A» (к примеру,«высоким артериальным давлением (АД)») и свойством «Б» (к примеру, «умеренно употребляет алкоголь»). В результате опроса всей группы участников требуется построить такой интегральный показатель, который бы количественно характеризовал связь между наличием признака «A» и наличием «Б» в популяции. Существует три характеристики такого рода и одна из них - это отношение шансов (ОШ), которая рассчитывается в три шага:

1. Для каждого наблюдения, обладающего свойством «Б», вычислить шансы того, что данное наблюдение обладает свойством «A».
2. Для каждого наблюдения, которое не обладает свойством «Б», вычислить шансы того, что данное наблюдение обладает свойством «A».
3. Разделить шансы, полученные в п.1, на шансы, полученные в п.2, — это и будет отношение шансов (ОШ).

Термин «участник» не обязательно обозначает человека, популяция может объединять любые объекты, как живой так и неживой природы.

Если ОШ превышает 1, наличие признака «А» ассоциируется с признаком «Б» в том смысле, что наличие «Б» повышает (по отношению к отсутствию «Б») шансы наличия «A».

Важное замечание: наличие повышенного ОШ (ОШ>1) не является свидетельством наличия причинной-следственной связи между «Б» и «A». Хотя в некоторых случаях признак "Б" может являться причиной признака "А" (к примеру, количество осадков и уровень воды в водоёме), ОШ определяет лишь тесноту связи между признаками.

Вполне возможен вариант наличия ложной связи, опосредованной некоторым другим свойством «C», которое индуцирует оба признака «A» и «Б» (Ложная корреляция). В нашем примере ложная корреляция могла бы проявиться так: в исследуемой группе добровольцев выявляется тенденция к снижению АД у лиц умеренно употребляющих алкоголь, но при попытке принуждения к употреблению алкоголя (в умеренных количествах, естественно) добровольцев, которые ранее алкоголь не принимали мы бы обнаружили, что АД у них в среднем не изменяется. Такие противоречивые результаты можно было бы объяснить, гипотетически, влиянием постороннего фактора: к примеру, в исследуемой группе представлены, в основном, лица давно и регулярно употребляющие алкоголь в умеренных количествах, у которых ярко выражены механизмы адаптации, которые, гипотетически, могут проявляться снижением АД. Таким образом, фактор "адаптация" является здесь посторонним.

Другие два способа количественной оценки связи двух качественных признаков — это относительный риск («ОР») и абсолютное снижение риска («АСР»). В клинических исследованиях и во многих других случаях, наибольший интерес представляет характеристика ОР, которая вычисляется аналогичным образом за исключением того, что вместо шансов используются вероятности. К сожалению, исследователи часто сталкиваются с ситуацией, когда имеющиеся данные позволяют рассчитать только ОШ, особенно это касается исследований типа случай-контроль. Тем не менее, когда один из признаков, например A, встречается достаточно редко («предположение о редком случае»), тогда ОШ для наличия «A» при условии, что участник обладает «Б» является хорошим приближением для ОР (требование «A при условии Б» обязательно, так как ОШ учитывает оба свойства симметрично, а ОР и другие характеристики — нет).

Говоря техническим языком, отношение шансов является мерой величины эффекта, описывающей силу связи или зависимости между двумя двузначными (бинарными) величинами. Она используется в качестве описательной статистики и играет важную роль в логистической регрессии.

Представим себе некое редкое заболевание, которым страдает, к примеру, только один среди многих тысяч взрослых людей в стране. Предположим, что существует некий фактор (например, определенная травма, полученная в детстве), который делает более вероятным развитие данного заболевания в будущем у взрослого. Наиболее информативным, в таком случае, был бы показатель отношения рисков (ОР). Но для его расчета мы должны бы были у всех взрослых в популяции узнать a) имели ли они травму в детстве и б) имеется ли у них заболевание сейчас. После этого мы получим информацию о том каково общее число человек, имевших травму в детстве (объем экспонированной группы) ${\displaystyle N_{E}}$, из которых ${\displaystyle D_{E}}$ заболели в будущем и ${\displaystyle H_{E}}$ остались здоровы; а также общее количество человек не имевших травму в детстве (объем неэкспонированной группы), ${\displaystyle N_{NE}}$, из которых ${\displaystyle D_{NE}}$ заболели и ${\displaystyle H_{NE}}$ остались здоровы. Поскольку ${\displaystyle N_{E}=D_{E}+H_{E}}$ и аналогичная сумма имеет место для «NE» индексов, мы имеем четыре независимых числа, которые можем записать в таблицу:

	Больны	Здоровы
Фактор присутствует (Пострадали)	${\displaystyle D_{E}}$	${\displaystyle H_{E}}$
Фактор отсутствует (Не пострадали)	${\displaystyle D_{NE}}$	${\displaystyle H_{NE}}$

Чтобы избежать недоразумений в дальнейшем подчеркнем, что все эти числа получены по генеральной совокупности, а не по выборке.

Теперь риск развития заболевания при наличии травмы будет ${\displaystyle D_{E}/N_{E}}$ (где ${\displaystyle N_{E}=D_{E}+H_{E}}$), а риск развития болезни при отсутствии травмы ${\displaystyle D_{NE}/N_{NE}}$. Относительный риск (ОР) — это отношение двух чисел:

${\displaystyle RR={\frac {D_{E}/N_{E}}{D_{NE}/N_{NE}}}\,,}$

которое можно переписать так ${\displaystyle RR={\frac {D_{E}N_{NE}}{D_{NE}N_{E}}}={\frac {D_{E}/D_{NE}}{N_{E}/N_{NE}}}.}$

Рассмотрим шансы развития заболевания, которые при наличии травмы будут ${\displaystyle D_{E}/H_{E}\,,}$, а при отсутствии травмы ${\displaystyle D_{NE}/H_{NE}}$. Отношение шансов (ОШ) — это отношение двух чисел: ${\displaystyle OR={\frac {D_{E}/H_{E}}{D_{NE}/H_{NE}}}\,,}$

которое можно переписать так ${\displaystyle OR={\frac {D_{E}H_{NE}}{D_{NE}H_{E}}}={\frac {D_{E}/D_{NE}}{H_{E}/H_{NE}}}.}$

Так как заболевание является редким ОР≈ОШ. В самом деле, для редкого заболевания имеем ${\displaystyle D_{E}\ll H_{E}}$ поэтому ${\displaystyle D_{E}+H_{E}\approx H_{E}}$, но ${\displaystyle D_{E}/(D_{E}+H_{E})\approx D_{E}/H_{E}}$, или другими словами, для экспонированной группы риск развития заболевания примерно равен шансам. Аналогичные рассуждения приводят нас к пониманию того, что риск примерно равен шансам для неэкспонированной группы; но тогда отношение рисков, коим является ОР, примерно равняется отношению шансов, чем и является ОШ. Можно также заметить, что предположение о редком заболевании говорит о том что ${\displaystyle N_{E}\approx H_{E}}$ и ${\displaystyle N_{NE}\approx H_{NE},}$ из чего следует ${\displaystyle N_{E}/N_{NE}\approx H_{E}/H_{NE},}$ или другими словами знаменатели в итоговых выражениях для ОР и ОШ примерно равны. Числители же в точности совпадают, и поэтому опять мы заключаем что ОШ≈ОР.

Если вернуться назад к нашему гипотетическому исследованию, очень часто возникающая проблема — это то что у нас может не оказаться нужной информации, чтобы оценить все эти четыре числа. Например, у нас может не оказаться данных обо всей популяции по фактам наличия или отсутствия травмы в детстве.

Часто мы можем обойти эту проблему путём случайной выборки из генеральной совокупности: а именно, если ни заболевание, ни подверженность травмам в детстве не являются редкими в популяции, мы можем случайным образом выбрать, скажем, сотню человек и найти эти четыре числа в данной выборке; предполагая, что эта выборка является достаточно репрезентативной, ОР, вычисленное в данной выборке, будет хорошим приближением к ОР для всей совокупности.

В то же время, некоторые заболевания могут быть настолько редкими что, при всем желании, даже в большой выборке может не оказаться ни одного заболевшего (или их может быть так мало, что о статистической значимости не может быть и речи). По этой причине расчет ОР становится невозможным. Но мы, тем не менее, можем получить оценку ОР в данных обстоятельствах поскольку в отличие от заболевания, экспонирование травмой в детстве не является редким событием. Разумеется, вследствие редкости заболевания, это также будет всего лишь оценкой ОР.

Взглянем на последнее выражение для ОР: дробь в числителе ${\displaystyle D_{E}/D_{NE}}$ мы в состоянии оценить, собрав все известные случаи заболевания (предполагается, что такие случаи есть, иначе мы не затевали бы исследование вообще), и посмотрев сколько среди заболевших людей были экспонированы, а сколько нет. И дробь в знаменателе ${\displaystyle H_{E}/H_{NE}}$ — это шансы того, что здоровый человек в популяции получил травму в детстве. Теперь заметим что эти шансы, на самом деле, можно оценить путём случайной выборки из популяции, так как было сказано ранее, что распространенность экспонирования травмой в детстве достаточно велика, вследствие чего случайная выборка достаточного объёма с большой долей вероятности будет содержать значительное количество экспонированных человек. Поэтому здесь заболевание очень редкое, но фактор, который его вызывает уже не такой редкий; похожие ситуации довольно часто встречаются на практике.

Таким образом, мы можем оценить ОШ и затем, используя редкость заболевания, утверждать, что эта оценка также является хорошим приближением для ОР. К слову, рассмотренный случай — это обычная задача исследования типа случай-контроль^[1].

Аналогичные рассуждения можно провести не прибегая к употреблению понятия ОШ, например, так: поскольку мы имеем соотношения ${\displaystyle N_{E}\approx H_{E}}$ и ${\displaystyle N_{NE}\approx H_{NE}}$, следовательно мы получим ${\displaystyle N_{E}/N_{NE}\approx H_{E}/H_{NE}}$. Поэтому если путём случайной выборки мы стремимся оценить соотношение ${\displaystyle H_{E}/H_{NE}}$, тогда, прибегнув к предположении о редкости заболевания получим, что его хорошей оценкой будет являться величина ${\displaystyle N_{E}/N_{NE}}$, что нам и требовалось(при этом ${\displaystyle D_{E}/D_{NE}}$ мы уже знаем после изучения нескольких случаев заболевания) получить для расчета ОР. Тем не менее, считается хорошим тоном при публикации результатов приводить значение ОШ, но с оговоркой о том что ОР примерно такой же.

Отношение шансов — это дробь, в числителе которой, стоят шансы некоторого события для одной группы, а в знаменателе шансы того же события, но для другой группы. Данное выражение применяется также для расчета выборочных оценок отношения. В качестве групп могут выступать мужчины и женщины, экспериментальная и контрольная группа, а также любая дихотомия. Если вероятность события в каждой группе обозначить за p₁ (первая группа) и p₂ (вторая группа), тогда отношение шансов будет равно:

${\displaystyle {p_{1}/(1-p_{1}) \over p_{2}/(1-p_{2})}={p_{1}/q_{1} \over p_{2}/q_{2}}={\frac {\;p_{1}q_{2}\;}{\;p_{2}q_{1}\;}},}$

где q_x = 1 − p_x. Отношение шансов равное 1 означает, что исследуемое событие обладает равными шансами в обеих группах. Отношение шансов превышающее 1 означает, что событие имеет больше шансов произойти в первой группе. И отношение шансов не превышающее 1 свидетельствует о том, что событие имеет меньше шансов в первой группе. Отношение шансов всегда неотрицательная величина (если его значение определено). Значение становится неопределенным, если p₂q₁ равно нулю, то есть, если p₂ равно нулю или q₁ равно нулю.

Отношение шансов можно определить через совместное распределение вероятностей двух бинарных случайных величин. Совместное распределение бинарных случайных величин X и Y задается таблицей

	Y = 1	Y = 0
X = 1	${\displaystyle p_{11}}$	${\displaystyle p_{10}}$
X = 0	${\displaystyle p_{01}}$	${\displaystyle p_{00}}$

где p₁₁, p₁₀, p₀₁ и p₀₀ неотрицательные совместные вероятности, сумма которых равна 1. Шансы для Y в двух группах, определяемых условиями X = 1 и X = 0 вычисляются с помощью условных вероятностей при условии X, то есть P(Y|X):

	Y = 1	Y = 0
X = 1	${\displaystyle p_{11}/(p_{11}+p_{10})}$	${\displaystyle p_{10}/(p_{11}+p_{10})}$
X = 0	${\displaystyle p_{01}/(p_{01}+p_{00})}$	${\displaystyle p_{00}/(p_{01}+p_{00})}$

Таким образом, отношение шансов будет равно

${\displaystyle {{\dfrac {p_{11}/(p_{11}+p_{10})}{p_{10}/(p_{11}+p_{10})}}{\bigg /}{\dfrac {p_{01}/(p_{01}+p_{00})}{p_{00}/(p_{01}+p_{00})}}}={\dfrac {p_{11}p_{00}}{p_{10}p_{01}}}.}$

Дробь в правой части выражения, выше, легко запомнить как произведение вероятностей согласованных ячеек (X = Y) деленное на произведение вероятностей рассогласованных ячеек (X ≠ Y). Несмотря на то, что обозначение категорий с помощью 0 и 1 является произвольным, правило согласованных и несогласованных ячеек остается в силе.

Если вычислить отношение шансов с помощью условных вероятностей при условии Y,

	Y = 1	Y = 0
X = 1	${\displaystyle p_{11}/(p_{11}+p_{01})}$	${\displaystyle p_{10}/(p_{10}+p_{00})}$
X = 0	${\displaystyle p_{01}/(p_{11}+p_{01})}$	${\displaystyle p_{00}/(p_{10}+p_{00})}$

мы получим тот же результат

${\displaystyle {{\dfrac {p_{11}/(p_{11}+p_{01})}{p_{01}/(p_{11}+p_{01})}}{\bigg /}{\dfrac {p_{10}/(p_{10}+p_{00})}{p_{00}/(p_{10}+p_{00})}}}={\dfrac {p_{11}p_{00}}{p_{10}p_{01}}}.}$

Остальные меры величины эффекта для бинарных данных, например относительный риск, не обладают таким свойством симметрии.

Если X и Y независимы, их совместные вероятности можно выразить через маргинальные вероятности p_x =  P(X = 1) и p_y =  P(Y = 1) следующим образом:

	Y = 1	Y = 0
X = 1	${\displaystyle p_{x}p_{y}}$	${\displaystyle p_{x}(1-p_{y})}$
X = 0	${\displaystyle (1-p_{x})p_{y}}$	${\displaystyle (1-p_{x})(1-p_{y})}$

В этом случае отношение шансов равняется единице, и наоборот, если отношение шансов равно единице, совместные вероятности можно представить в виде таких произведений. Таким образом, отношение шансов равняется единице тогда и только тогда, когда X и Y независимы.

Отношение шансов является функцией от совместных вероятностей, и обратно, совместные вероятности можно восстановить если известны отношение шансов и маргинальные вероятности

P(X = 1) = p₁₁ + p₁₀ и P(Y = 1) = p₁₁ + p₀₁. Если отношение шансов R отлично от 1, то:

${\displaystyle p_{11}={\frac {1+(p_{1\cdot }+p_{\cdot 1})(R-1)-S}{2(R-1)}}}$

где p_1• = p₁₁ + p₁₀,  p_•1 = p₁₁ + p₀₁ и

${\displaystyle S={\sqrt {(1+(p_{1\cdot }+p_{\cdot 1})(R-1))^{2}+4R(1-R)p_{1\cdot }p_{\cdot 1}}}.}$

В случае равенства R = 1, мы имеем независимость, поэтому p₁₁ = p_1•p_•1.

Так как мы знаем p₁₁, остальные три вероятности легко определяются из маргинальных.

Предположим, что в выборке из 100 мужчин 90 употребляли вино на прошлой неделе, в то же время в выборке из 100 женщин только 20 употребляли вино за тот же период. Шансы того, что мужчина употреблял вино составляют 90 к 10, или 9:1, тогда как те же шансы для женщин только 20 к 80, или 1:4 = 0,25:1. Отношение шансов составит величину 9/0,25, или 36, которая показывает нам, что значительно большее число именно мужчин употребляют вино. Более подробные расчеты:

${\displaystyle {0,9/0,1 \over 0,2/0,8}={\frac {\;0,9\times 0,8\;}{\;0,1\times 0,2\;}}={0,72 \over 0,02}=36.}$

Данный пример показывает, как сильно различаются отношения шансов в разных системах расчета: в выборке употреблявших вино, мужчин в 90/20 = 4,5 раза больше чем женщин, но при этом у них в 36 раз больше шансов. Логарифм отношения шансов, разница логитов вероятностей, смягчает этот эффект и придает свойство симметрии по отношению к порядку групп. Например, применив натуральный логарифм к отношению шансов 36/1, мы получим 3,584, а сделав то же самое с отношением 1/36, получим −3,584.

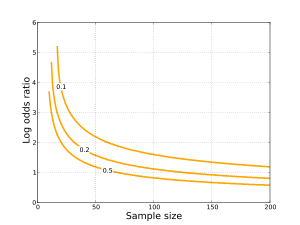
Было разработано несколько подходов для проверки статистических гипотез об отношении шансов.

Один из подходов основан на аппроксимации выборочного распределения логарифма отношения шансов (а именно, натурального логарифма отношения шансов). Если использовать обозначения в терминах совместных вероятностей, логарифм генерального отношения шансов будет равен

${\displaystyle {\log \left({\frac {p_{11}p_{00}}{p_{01}p_{10}}}\right)=\log(p_{11})+\log(p_{00}{\big )}-\log(p_{10})-\log(p_{01})}.}$

Если мы представим результаты эксперимента в виде таблицы сопряженности

	Y = 1	Y = 0
X = 1	${\displaystyle n_{11}}$	${\displaystyle n_{10}}$
X = 0	${\displaystyle n_{01}}$	${\displaystyle n_{00}}$

оценки вероятностей для совместного распределения можно определить так:

	Y = 1	Y = 0
X = 1	${\displaystyle {\hat {p}}_{11}}$	${\displaystyle {\hat {p}}_{10}}$
X = 0	${\displaystyle {\hat {p}}_{01}}$	${\displaystyle {\hat {p}}_{00}}$

где p̂_ij = n_ij / n, а n = n₁₁ + n₁₀ + n₀₁ + n₀₀ является суммой значений всех четырёх ячеек таблицы. Логарифм выборочного отношения шансов будет равен:

${\displaystyle {L=\log \left({\dfrac {{\hat {p}}_{11}{\hat {p}}_{00}}{{\hat {p}}_{10}{\hat {p}}_{01}}}\right)=\log \left({\dfrac {n_{11}n_{00}}{n_{10}n_{01}}}\right)}}$.

Распределение логарифма отношения шансов хорошо аппроксимируется нормальным распределением с параметрами:

${\displaystyle X\ \sim \ {\mathcal {N}}(\log(OR),\,\sigma ^{2}).}$

Стандартная ошибка логарифма отношения шансов оценивается по формуле

${\displaystyle {{\rm {SE}}={\sqrt {{\dfrac {1}{n_{11}}}+{\dfrac {1}{n_{10}}}+{\dfrac {1}{n_{01}}}+{\dfrac {1}{n_{00}}}}}}}$.

Данное приближение является асимптотическим, и поэтому может давать бессмысленный результат если какая-либо из ячеек содержит слишком малое число. Если обозначить за L логарифм выборочного отношения шансов, приближенная оценка 95 % доверительного интервала для логарифма генерального отношения шансов будет определяться в рамках нормальной модели так: L ± 1.96SE^[2]. От логарифма можно избавиться, воспользовавшись преобразованием exp(L − 1.96SE), exp(L + 1.96SE), и получить 95 % доверительный интервал для отношения шансов. Если требуется проверить гипотезу о равенстве генерального отношения шансов единице, можно определить двустороннее значение p-статистики как 2P(Z< −|L|/SE), где P означает вероятность, а Z — это величина, обладающая стандартным нормальным распределением.

Другой подход позволяет в некоторой степени восстановить исходное распределение выборочного отношения шансов. Для этого фиксируются маргинальные частоты признаков X и Y, а значения в ячейках таблицы меняются последовательно либо случайно. Легко понять, что изменению подлежит только одна из ячеек таблицы, поскольку все остальные определяются исходя из условия постоянства маргинальных частот.

Логистическая регрессия — это один из способов определения отношения шансов для двух бинарных переменных. Предположим, имеется одна зависимая двоичная переменная Y, одна независимая бинарная переменная X (предиктор), и группа дополнительных предикторов Z₁, …, Z_p, которые могут принимать какие угодно значения. Если мы будем использовать множественную логистическую регрессию Y на X, Z₁, …, Z_p, оценка коэффициента ${\displaystyle {\hat {\beta }}_{x}}$ для X имеет связь с условным отношением шансов. А именно, на уровне генеральной совокупности

${\displaystyle \exp(\beta _{x})={\frac {P(Y=1|X=1,Z_{1},\ldots ,Z_{p})/P(Y=0|X=1,Z_{1},\ldots ,Z_{p})}{P(Y=1|X=0,Z_{1},\ldots ,Z_{p})/P(Y=0|X=0,Z_{1},\ldots ,Z_{p})}},}$

поэтому ${\displaystyle \exp({\hat {\beta }}_{x})}$ — это оценка данного условного отношения шансов. Величина ${\displaystyle \exp({\hat {\beta }}_{x})}$, в таком случае, интерпретируется как оценка отношения шансов между Y и X при фиксированных значениях переменных Z₁, …, Z_p.

Когда данные представляют собой репрезентативную выборку, вероятности в ячейках таблицы p̂_ij интерпретируются как частоты каждой из четырёх групп в генеральной совокупности согласно комбинациям значений X и Y. Во многих случаях использование репрезентативной выборки является непрактичным, поэтому часто формируется селективная выборка. Например, в выборку отбираются объекты у которых X = 1 с заданной вероятностью f, несмотря на их реальную частоту в генеральной совокупности (вследствие этого, неизбежно, объекты со свойством X = 0 будут отобраны с вероятностью 1 − f). В таком случае, мы получим следующие совместные вероятности:

	Y = 1	Y = 0
X = 1	${\displaystyle fp_{11}/(p_{11}+p_{10})}$	${\displaystyle fp_{10}(p_{11}+p_{10})}$
X = 0	${\displaystyle (1-f)p_{01}/(p_{01}+p_{00})}$	${\displaystyle (1-f)p_{00}/(p_{01}+p_{00})}$

Отношение шансов p₁₁p₀₀ / p₀₁p₁₀ для данного распределения не зависит от f. Этот пример показывает, что отношение шансов (и, соответственно, логарифм отношения шансов) инвариантно к неслучайным относительно одной из изучаемых переменных выборкам. Однако, стоит заметить, что стандартная ошибка логарифма отношения шансов зависит от f.

Свойство инвариантности используется в двух очень важных ситуациях:

• Предполагается неудобным или непрактичным получение репрезентативной выборки, но при этом возможно получить подходящую выборку объектов с разными значениями X, такую что среди подвыборок X = 0 и X = 1 значения Y являются репрезентативными для генеральной совокупности (например, они соответствуют истинным условным вероятностям).
• Предполагается сильный перекос маргинального распределения одной из переменных, скажем, X. Например, при изучении связи между высоким уровнем потребления алкоголя и раком поджелудочной железы, встречаемость рака может быть очень низкой, поэтому для получения хоть некоторого числа случаев рака может потребоваться очень большая репрезентативная выборка. Тем не менее, мы можем использовать госпитальные данные для контакта с большинством или со всеми пациентами, страдающими раком поджелудочной железы, а затем получить случайную выборку такого же числа субъектов без рака железы (такое исследование носит название «случай-контроль»).

В обеих ситуациях отношение шансов можно без смещения оценить по данным селективной выборки.

В виду широкого распространения логистической регрессии, отношение шансов часто используется в медицинских и социальных исследованиях. Отношение шансов обычно используется в анкетировании, эпидемиологии, а также для представления результатов таких клинических испытаний как случай-контроль. В отчетах оно чаще всего сокращенно обозначается как «OR». В случае, когда объединяются результаты нескольких опросов, используется название «pooled OR».

В клинических и других исследованиях, больший интерес представляет характеристика относительного риска нежели отношения шансов. Относительный риск лучше всего определяется по генеральной совокупности, но если справедливо предположение о редком заболевании, отношение шансов является хорошим приближением для оценки относительного риска — шансы это дробь вида p / (1 − p), поэтому когда p приближается к нулю, 1 − p приближается к единице, что означает приближение шансов к величине риска, а, следовательно, приближение отношения шансов к относительному риску^[3]. Когда предположение о редком заболевании не может быть признано справедливым, отношение шансов может переоценивать относительный риск^[4][5][6].

Если в контрольной группе известна величина абсолютного риска, переход от одной величины к другой осуществляется через выражение:^[4]

${\displaystyle RR\approx {\frac {OR}{1-R_{C}+(R_{C}\times OR)}}}$

где:

• RR = относительный риск
• OR = отношение шансов
• R_C = абсолютный риск в неэкспонированной группе, заданный в виде дроби (например, величина риска 10 % вводится в формулу как  0,1)

В медицинской литературе отношение шансов часто путают с величиной относительного риска. Для аудитории нестатистиков, концепция отношения шансов трудна для понимания, поэтому производит более впечатляющий эффект на читателя^[7]. Тем не менее, большинство авторов считают, что относительный риск легко доступен для понимания^[8]. В одном из исследований сказано, что члены национального фонда борьбы с заболеванием в 3,5 раза чаще всех остальных знали об общих принципах лечения данного заболевания, но отношение шансов было 24 и в статье это было представлено как то, что члены данной организации «более чем в 20 раз чаще знают о лечении»^[9]. Исследование статей в двух журналах показало что в 26 % статей отношение шансов интерпретировалось как отношение рисков^[10].

Это может свидетельствовать о том, что авторы, не имеющие представления о сути данной величины, предпочитают её как наиболее выразительную для своей публикации^[8]. Но её использование в некоторых случаях может вводить в заблуждение^[11]. Ранее было сказано, что отношение шансов должно описывать меру эффекта когда нет возможности оценить отношение рисков непосредственно^[7].

Ещё одна уникальная особенность отношения шансов — свойство непосредственной математической обратимости, например, в зависимости от постановки задачи: изучить свободу от некоторого заболевания или изучить наличие этого заболевания, ОШ для свободы от заболевания есть величина обратная (или 1/ОШ) к ОШ для наличия заболевания. Это свойство «инвариантности отношения шансов», которым не обладает величина относительного риска. Рассмотрим его на примере:

предположим, в клиническом исследовании получен риск случая 4/100 в группе, принимавшей препарат и 2/100 в группе плацебо, то есть получены ОР = 2 и ОШ = 2,04166 для случая при сравнении групп препарат-плацебо. С другой стороны, если обратить анализ и исследовать риск неслучая, тогда в группе, принимавшей препарат, риск неслучая будет 94/100, а в группе плацебо 98/100, то есть ОР = 0,9796 для неслучая при сравнении групп препарат-плацебо, но ОШ = 0,48979. Как можно увидеть, ОР = 0,9796 не является величиной обратной к ОР = 2. Напротив, ОШ = 0,48979, на самом деле, является величиной обратной к ОШ = 2,04166.

Это и есть свойство «инвариантности отношения шансов», из-за которого ОР для свободы от события не совпадает для ОР для риска события, тогда как ОШ обладает этим свойством симметрии при анализе свободы или риска. Опасность для клинической интерпретации ОШ возникает, когда вероятность случая высока, при этом преувеличиваются имеющиеся различия, если предположение о редком заболевании не выполняется. С другой стороны, когда заболевание действительно является редким, использование ОР для описания свободы (например, ОР = 0,9796 из примера выше) может скрыть клинический эффект удвоения риска для события при приеме препарата или при экспонировании.

Выборочное отношение шансов n₁₁n₀₀ / n₁₀n₀₁ легко рассчитывается, и для умеренных и больших выборок дает хорошую оценку генерального отношения шансов. Когда одна или несколько ячеек в таблице сопряженности содержит маленькое значение, отношение шансов может стать смещенным и приобрести большую дисперсию. Было предложено несколько альтернативных оценок отношения шансов, обладающих в таких условиях лучшими свойствами. Одна из альтернатив — это оценка условного максимального правдоподобия, которая опирается на суммы строк и столбцов при определении функции правдоподобия, подлежащей максимизации (так же, как это делается при выполнении точного теста Фишера)^[12]. Альтернатива — это оценка Мантеля-Хензеля.

Следующие четыре таблицы сопряженности содержат совместные абсолютные частоты, а также соответствующие выборочные отношения шансов (OR) и логарифмы выборочных отношений шансов (LOR):

Следующие таблицы совместных распределений содержат генеральные совместные вероятности, а также соответствующие генеральные отношения шансов (OR) и логарифмы генеральных отношений шансов (LOR):

• Уровень опасности в анализе выживаемости
• Относительный риск

• Простой калькулятор для вычисления отношения шансов — сайт
• Калькулятор отношения шансов с различными тестами — сайт
• Интернет-приложение OpenEpi, которое вычисляет отношение шансов для разных ситуаций