Отображение тент
Отображение тент в теории динамических систем задаётся следующим образом:
Для значений отображение тент переводит отрезок в себя, являясь динамической системой c дискретным временем. В частности, орбитой точки из интервала является последовательность :

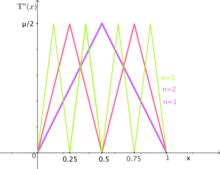
Несмотря на то, что отображение тент является довольно простой нелинейной динамической системой, оно демонстрирует ряд свойств, характерных и для более сложных систем: плотность периодических орбит, перемешивание, чувствительность к начальным условиям, т.е. хаотичность[1].
Свойства

- Если , является притягивающей неподвижной точкой: система будет стремиться к нулю с устремлением времени в бесконечность при любом исходном значении из отрезка .
- Если , все — неподвижные точки, а — предпериодические точки единичного периода (после одной итерации переходят в неподвижные).
- Если , то отображение имеет две неподвижные точки: и . Причем обе из них будут неустойчивыми, то есть значения , лежащие в окрестностях неподвижных точек, будут отдаляться от них с последующими итерациями. Более того, для таких значений , в интервале содержатся и периодические, и непериодические точки.
- Если , то система отображает множество интервалов из отрезка в себя, и их объединение является множеством Жюлиа отображения тент, т.е. множеством точек, чьи орбиты неустойчивы.
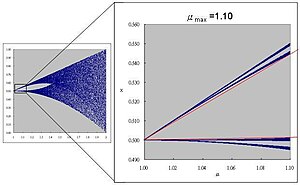
- увеличение показывает, что при μ ≈ 1, множество Жюлиа состоит из нескольких интервалов. На диаграммах видно 4 и 8 интервалов при достаточном увеличении.
 Бифуркационная диаграмма отображения тент. Более высокая плотность соответствует более высокой вероятности, что переменная x примет данное значение для параметра
Бифуркационная диаграмма отображения тент. Более высокая плотность соответствует более высокой вероятности, что переменная x примет данное значение для параметра- При увеличении вблизи острия видно 4 интервала
- При дальнейшем увеличении видно 8 интервалов

- Если , то интервалы из отрезка сходятся и множество Жюлиа — это весь интервал (см. бифуркационную диаграмму).

- Если , то система переводит отрезок [0;1] в себя. В этом случае периодические точки плотны на отрезке, так что отображение демонстрирует хаотичность[2]. Непериодическое поведение характерно только для иррациональных чисел, что может быть показано с помощью механизма, которым отображение действует на представленное в двоичной записи число: оно перемещает двоичную запятую вправо на один знак, а затем, если то, что оказалось слева от запятой — это единица, отбрасывает её и обращает все единицы в нули и наоборот (кроме последней единицы для чисел с конечной двоичной записью). Для иррационального числа, двоичная запись которого непериодична, это бесконечный процесс. Кроме того, стоит обратить внимание, что для отображение тент топологически сопряжено логистическому отображению для и полусопряжен отображению удвоения, что указывает на сходство динамических свойств этих отображений[3]. Действительно, пусть — орбита отображения тент при , а — орбита логистического отображения для , тогда они связаны соотношением: .
- Если , множество Жюлиа отображения все еще содержит бесконечное количество и периодических, и непериодических точек, но почти всюду точки отрезка стремятся к бесконечности. Само множество становится канторовым. В частности, множество Жюлиа отображения тент для — стандартное канторово множество.
Асимметричное отображение тент
Также объектом изучения теории динамических систем является асимметричное отображение тент . Его можно считать расширением случая стандартного отображения тент:
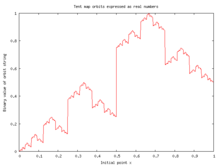
Асимметричное отображение тент сохраняет вид кусочно-линейной функции и может быть использовано для представления вещественных чисел из по аналогии с десятичной записью[4].
См. также
- Функция (математика)
- Отображение удвоения
- Логистическое отображение
- Динамическая система
- Порядок Шарковского
- Постоянная Фейгенбаума
- Аттрактор
Литература
- ↑ Lynch, Stephen. "Nonlinear discrete dynamical systems." Dynamical Systems with Applications using Maple. Birkhäuser Boston, 2010. 263-295.
- ↑ Li, Tien-Yien, and James A. Yorke. "Period three implies chaos." American mathematical monthly (1975): 985-992.
- ↑ Smale, Stephen, Morris W. Hirsch, and Robert L. Devaney. "Discrete dynamical systems." Differential equations, dynamical systems, and an introduction to chaos. Vol. 60. Academic Press, 2003. 327-357.
- ↑ Lagarias, J. C., H. A. Porta, and K. B. Stolarsky. "Asymmetric tent map expansions. I. Eventually periodic points." Journal of the London Mathematical Society 2.3 (1993): 542-556.

![{\displaystyle \mu \in [0;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6048ddab6ac04b286f05e02c694f956f291491e6)
![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)









![{\displaystyle x\in [0;0.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea123b4b748d1b42c30ae6e288d2b6b1b21c8b1a)
![{\displaystyle x\in (0.5;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27bd27ae3f95008a10cc7c1541369bc072a4c252)
![{\displaystyle \mu \in (1;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0106226fa00821ea8733ecaf445dc0f6c1387233)


![{\displaystyle x\in [\mu -{\mu ^{2}}/2;{\mu }/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447abc02b259acd607f3f9e53440af68bda7a99e)
![{\displaystyle \mu \in (1;{\sqrt {2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c21cc2362520d7912c2917090fd744057d6b0edb)
![{\displaystyle [\mu -{\mu ^{2}}/2;{\mu }/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3e9a1b7f3302530560196ecda10aaf9fe51564)


![{\displaystyle \mu \in ({\sqrt {2}};2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d6cb1d5266c8df3dc81352fbe07bc021ede938d)






![{\displaystyle f_{\alpha }:[0;1]\rightarrow [0;1],\alpha \in (1;+\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f2ee06af0952726ab8e37dd953b74cc034319cc)












