Параллакс Солнца

Параллакс Солнца, суточный параллакс Солнца (π_☉) — горизонтальный экваториальный параллакс Солнца, угол, под которым со среднего расстояния Солнца виден экваториальный радиус Земли^[1].

До 1964 года являлся фундаментальной астрономической постоянной и считался равным 8,80″^[2]. С принятием в 1964 году астрономическим союзом новой системы единиц π_☉ является производной постоянной, и составляет 8,794".^[1]

Методы определения параллакса Солнца разделяются на геометрические (тригонометрические), динамические (гравитационные) и физические.

Теория геометрических методов разработана в 1677 Эдмундом Галлеем. В их основе лежат астрометрические измерения положений небесных тел относительно звёзд. Измерения могут быть получены одновременно на двух разных обсерваториях, лежащих почти на одном меридиане и достаточно удалённых по широте, либо на одной, но в различные часы суток, используя перемещение наблюдателя в пространстве вследствие суточного вращения Земли.

В качестве небесных тел, чьи измеренные положения использовались для вычисления π_☉, в разные эпохи брались^[1]:

• Марс (начиная со 2-й половины XVII века);
• Венера и её прохождение по диску Солнца (1761, 1769, 1874 и 1882 года)
• Малые планеты, в том числе Эрос, Икар и Географ, чьи координаты определялись фотографическими наблюдениями (с конца XIX века).

Динамические методы определения параллакса Солнца основаны на изучении возмущений в движении планет и Луны, вызываемых притяжением других небесных тел. Измеренное расстояние до небесного тела R₀ сравнивается с R_с, вычисленным на основе эфемерид. В результате одного наблюдения получается условное уравнение относительно элементов орбиты планеты^[2]:

${\displaystyle R_{0}-R_{c}=\sum \limits _{k=1}^{6}{\frac {\partial R_{k}}{\partial p_{k}}}\Delta p_{k}+\epsilon }$

И полагают, что поправка к большой полуоси орбиты планеты вызвана неточностью астрономической единицы и, соответственно, параллакса Солнца.

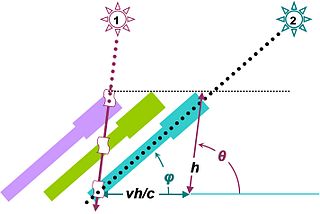
В основе физических методов определения лежит соотношение средней скорости движения Земли по гелиоцентрической орбите (V₀≈29,8 км/с) и большой полуоси орбиты.

V₀ можно определить измеряя лучевые скорости звёзд, лежащих вблизи эклиптики; определяя постоянную годичной аберрации; измеряя доплеровские смещения радиолиний (с длиной волны 21 см) в спектрах межзвёздных водородных облаков.

Большую полуось можно получить методами радиолокации измеряя расстояния между Землёй и планетами, Луной, космическими зондами.

• Блажко С. Н. Курс сферической астрономии. — 2. — М.— Л., 1954.;
• Идельсон Н. И. Фундаментальные постоянные астрономии и геодезии, в кн.: Астрономический ежегодник СССР на 1942 год. — М.— Л., 1941.;
• Куликов К. А. Фундаментальные постоянные астрономии. — М., 1956.;
• Фундаментальные постоянные астрономии (Материалы 21 Симпозиума Международного астрономического союза 21 августа 1961). — М., 1967.;
• Lilley Е., Brouwer D. The solar parallax and the hydrogen line (англ.) // The Astronomical Journal. — IOP Publishing, 1959. — Vol. 64, no. 8. — Bibcode: 1959AJ.....64R.338L.