Стати́стика — отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме.

Вероя́тность — степень возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднена. Возможны различные градации «уровней» вероятности.
Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез, основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Прогно́з — это научно обоснованное суждение о возможных состояниях объекта в будущем и (или) об альтернативных путях и сроках их осуществления. В узком смысле, это вероятностное суждение о будущем состоянии объекта исследования.
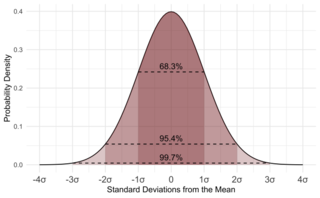
Среднеквадрати́ческое отклонение — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. Обычно означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.
Описательная статистика или дескриптивная статистика занимается обработкой эмпирических данных, их систематизацией, наглядным представлением в форме графиков и таблиц, а также их количественным описанием посредством основных статистических показателей.
Довери́тельный интерва́л — термин, используемый в математической статистике при интервальной оценке статистических параметров, более предпочтительной при небольшом объёме выборки, чем точечная. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Фидуциальный вывод, как разновидность статистического вывода, был впервые предложен сэром Р. Э. Фишером.
Статистика — измеримая числовая функция от выборки, не зависящая от неизвестных параметров распределения элементов выборки.
Точный тест Фишера — тест статистической значимости, используемый в анализе таблиц сопряжённости для выборок маленьких размеров. Относится к точным тестам значимости, поскольку не использует приближения большой выборки.
Статистическая оценка — это статистика, которая используется для оценивания неизвестных параметров распределений случайной величины.
Критерий Лиллиефорса — статистический критерий, названный по имени Хьюберта Лиллиефорса, профессора статистики Университета Джорджа Вашингтона, являющийся модификацией критерия Колмогорова–Смирнова. Используется для проверки нулевой гипотезы о том, что выборка распределена по нормальному закону для случая, когда параметры нормального распределения априори неизвестны.
Z-тест — класс методов статистической проверки гипотез, основанных на нормальном распределении. Обычно применяется для проверки равенства средних значений при известной дисперсии генеральной совокупности или при оценке выборочного среднего стандартизованных значений. Z-статистика вычисляется как отношение разницы между случайной величиной и математическим ожиданием к стандартной ошибке этой случайной величины:


В математической статистике и теории принятия решений байесовская оценка решения — это статистическая оценка, минимизирующая апостериорное математическое ожидание функции потерь. Иначе говоря, она максимизирует апостериорное математическое ожидание функции полезности. В рамках теории Байеса данную оценку можно определить как оценку апостериорного максимума.
Теория оценивания — раздел математической статистики, решающий задачи оценивания непосредственно не наблюдаемых параметров сигналов или объектов наблюдения на основе наблюдаемых данных. Для решения задач оценивания применяется параметрический и непараметрический подход. Параметрический подход используется, когда известна математическая модель исследуемого объекта и характер возмущений и требуется лишь определить в ней неизвестные параметры. В этом случае используются метод наименьших квадратов, метод максимального правдоподобия и метод моментов. Непараметрический подход используется для изучения объектов неизвестной структуры и с неизвестными возмущениями. Теория оценивания применяется в приборах для физических и других измерений, при моделировании физических, экономических, биологических и других процессов.
Непараметрическая статистика — раздел статистики, который не основан исключительно на параметризованных семействах вероятностных распределений. Непараметрическая статистика включает в себя описательную статистику и статистический вывод.
Статистический параметр или параметр совокупности — это величина, которая индексирует семейство распределений вероятностей. Его можно расценивать как числовую характеристику совокупности или статистической модели.

В статистике методы Монте-Карло с марковскими цепями (англ. MCMC) — это класс алгоритмов для семплирования, моделирующих некоторое распределение вероятностей. Построив марковскую цепь, которая имеет целевое распределение в качестве своего равновесного, можно получить выборку с тем же распределением путем записи состояний цепи. Чем больше шагов будет использовано, тем ближе распределение выборки будет к целевому. Для построения цепей используются различные алгоритмы, например, алгоритм Метрополиса-Гастингса.
Критерий Вальда — Вольфовица, названный в честь статистиков Абрахама Вальда и Джейкоба Вольфовица, представляет собой непараметрический статистический тест, который проверяет гипотезу о случайности для двух последовательностей данных одинаковой длины. Точнее, данный критерий можно использовать для проверки нулевой гипотезы о том, что элементы двух последовательностей взаимно независимы.



