Плотность
| Плотность | |
|---|---|
| Размерность | L−3 M |
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина | |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:
- .
Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:
- средняя плотность тела — отношение массы тела к его объёму . В однородном случае она называется просто плотностью тела (или плотностью вещества, из которого это тело состоит);
- плотность тела в точке — предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда объём стремится к нулю[1], или, кратко, . Так как на атомарном уровне любое тело неоднородно, при предельном переходе нужно остановиться на объёме, соответствующем используемой физической модели.
Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.
Для обозначения плотности обычно используется греческая буква (ро) (происхождение обозначения подлежит уточнению), иногда используются латинские буквы D и d (от лат. densitas «плотность»). Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.
Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.
Формула нахождения плотности
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где M — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.
При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:
где — молярная масса газа, — молярный объём (при стандартных условиях приближённо равен 22,4 л/моль).
Плотность тела в точке записывается как
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
Случай сыпучих и пористых тел
В случае сыпучих и пористых тел различают
- истинную плотность, определяемую без учёта пустот;
- насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[2].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
- Гранит имеет плотность 2600 кг/м³.
- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность золота 19320 кг/м³.
- Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
- Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным[] физическим представлениям — это планковская плотность 5,1⋅1096 кг/м³.
Плотности астрономических объектов
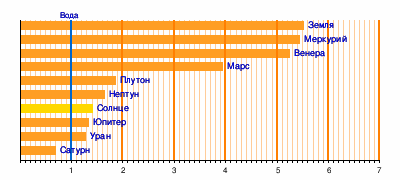
- Средние плотности небесных тел Солнечной системы см. на врезке.
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
- Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[6]
- ,
где:
- — давление,
- — молярная масса,
- — универсальная газовая постоянная, равная приблизительно 8,314 Дж/(моль·К)
- — термодинамическая температура.
Плотности некоторых жидкостей
| Бензин | 710 | Молоко | 1040 |
| Вода (4 °C) | 1000 | Ртуть (0 °C) | 13600 |
| Керосин | 820 | Диэтиловый эфир | 714 |
| Глицерин | 1260 | Этанол | 789 |
| Морская вода | 1030 | Скипидар | 860 |
| Масло оливковое | 920 | Ацетон | 792 |
| Масло моторное | 910 | Серная кислота | 1835 |
| Нефть | 550—1050 | Жидкий водород (−253 °C) | 70 |
Плотность некоторых пород древесины
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
| Осмий | 22610[7] | Родий | 12410[8] | Хром | 7190[9] |
| Иридий | 22560[10] | Палладий | 12020[11] | Германий | 5320[12] |
| Плутоний | 19840[13] | Свинец | 11350[14] | Алюминий | 2700[15] |
| Платина | 19590[16] | Серебро | 10500[17] | Бериллий | 1850[18] |
| Золото | 19300[14] | Никель | 8910[19] | Рубидий | 1530[20] |
| Уран | 19050[21] | Кобальт | 8860[22] | Натрий | 970[23] |
| Тантал | 16650[24] | Медь | 8940[25] | Цезий | 1840[26] |
| Ртуть | 13530[27] | Железо | 7870[28] | Калий | 860[29] |
| Рутений | 12450[30] | Марганец | 7440[31] | Литий | 530[32] |
Измерение плотности
Для измерений плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Различные виды ареометров — измерители плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
- Метод гидростатического взвешивания.
Остеоденситометрия — процедура измерения плотности костной ткани человека.
См. также
- Список химических элементов с указанием их плотности
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
- Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
- Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. . Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- ↑ Planetary Fact Sheet Архивировано 14 марта 2016 года. (англ.)
- ↑ Sun Fact Sheet Архивная копия от 15 июля 2010 на Wayback Machine (англ.)
- ↑ Stern, S. A., et al. The Pluto system: Initial results from its exploration by New Horizons (англ.) // Science : journal. — 2015. — Vol. 350, no. 6258. — P. 249—352. — doi:10.1126/science.aad1815.
- ↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72. Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Дата обращения: 4 января 2019. Архивировано 23 ноября 2018 года.
- ↑ Krebs, 2006, p. 158.
- ↑ Krebs, 2006, p. 136.
- ↑ Krebs, 2006, p. 96.
- ↑ Krebs, 2006, p. 160.
- ↑ Krebs, 2006, p. 138.
- ↑ Krebs, 2006, p. 198.
- ↑ Krebs, 2006, p. 319.
- ↑ 1 2 Krebs, 2006, p. 165.
- ↑ Krebs, 2006, p. 179.
- ↑ Krebs, 2006, p. 163.
- ↑ Krebs, 2006, p. 141.
- ↑ Krebs, 2006, p. 67.
- ↑ Krebs, 2006, p. 108.
- ↑ Krebs, 2006, p. 57.
- ↑ Krebs, 2006, p. 313.
- ↑ Krebs, 2006, p. 105.
- ↑ Krebs, 2006, p. 50.
- ↑ Krebs, 2006, p. 151.
- ↑ Krebs, 2006, p. 111.
- ↑ Krebs, 2006, p. 60.
- ↑ Krebs, 2006, p. 168.
- ↑ Krebs, 2006, p. 101.
- ↑ Krebs, 2006, p. 54.
- ↑ Krebs, 2006, p. 134.
- ↑ Krebs, 2006, p. 98.
- ↑ Krebs, 2006, p. 47.
Литература
- Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
- Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
- Krebs R. E. . The History and Use of Our Earth's Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки
- Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
- Подробная таблица значений плотности распространённых жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
- Урок по теме "Плотность вещества" Архивная копия от 30 января 2022 на Wayback Machine