Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки, в зависимости от подхода, круг может включать или не включать.

Ли́нза — деталь из прозрачного однородного материала, имеющая две преломляющие полированные поверхности, например, обе сферические или же одну плоскую, а другую — сферическую. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, кристаллы, оптически прозрачные пластмассы и другие материалы.

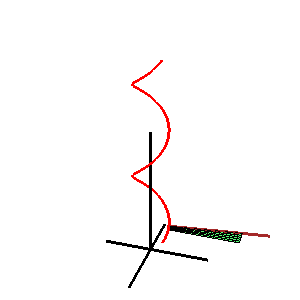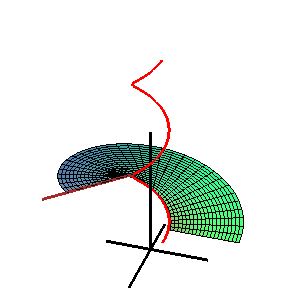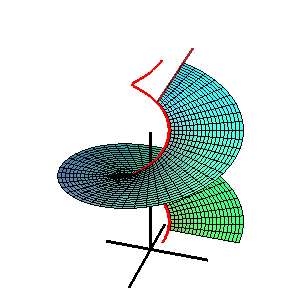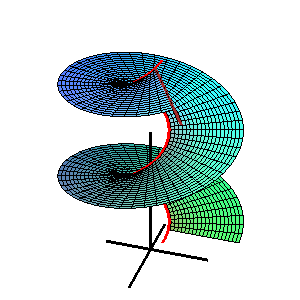
Коно́ид — линейчатая поверхность, у которой образующие пересекают фиксированную прямую — ось коноида. Если все образующие коноида перпендикулярны его оси, то такой коноид называют прямым.

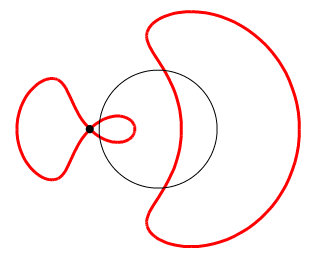
Улитка Паскаля ― плоская кривая определённого типа. Названа по имени Этьена Паскаля, впервые рассмотревшего её.
Линейчатая поверхность ― поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

Поде́ра кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривой.

Антиподе́ра кривой относительно точки — кривая, для которой данная кривая есть подера относительно той же точки.

Изгибаемый многогранник — многогранник, чью пространственную форму можно изменить непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров, а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника.

Фёдор Алексеевич Богомолов — советский и американский математик, известный своими работами по алгебраической геометрии и теории чисел.

Выпуклая кривая — кривая на евклидовой плоскости, которая лежит по одну сторону от любой касательной прямой.

Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Теорема Римана — Роха связывает комплексный анализ связных компактных римановых поверхностей с чисто топологическим родом поверхности g, используя методы, которые могут быть распространены на чисто алгебраические ситуации.

Поверхность Шерка является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году. Его первая поверхность является дважды периодической поверхностью, а вторая — просто периодической. Они были третьим нетривиальным примером минимальных поверхностей. Две поверхности сопряжены друг другу.

В дифференциальной геометрии Минимальная поверхность Каталана — это минимальная поверхность, которую впервые исследовал Эжен Шарль Каталан в 1855 г..

Неявная поверхность — это поверхность в евклидовом пространстве, определённая уравнением


Поверхности постоянной средней кривизны — класс поверхностей моделирующий поверхности мыльных плёнок разделяющие области с фиксированной разницей давлений. В частном случае, если давление с обеих сторон равно, модель определяет минимальные поверхности.
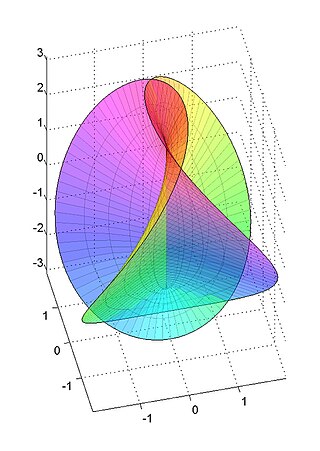
Поверхность Хеннеберга — неориентируемая минимальная поверхность, названная именем немецкого математика Лебрехта Хенненберга.

Параметризация Вейерштрасса — Эннепера минимальных поверхностей — классический раздел дифференциальной геометрии.