
Сфе́ра — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки.

Градие́нт — вектор, своим направлением указывающий направление наискорейшего роста некоторой скалярной величины  .
.
Диверге́нция — дифференциальный оператор, отображающий векторное поле на скалярное, который определяет, «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Фу́нкция Гри́на — функция, используемая для решения линейных неоднородных дифференциальных уравнений с граничными условиями . Названа в честь английского математика Джорджа Грина, который первым развил соответствующую теорию в 1830-е годы.
Лагранжева механика — формулировка классической механики, введённая Луи Лагранжем в 1788 году. В лагранжевой механике траектория объекта получается при помощи отыскания пути, который минимизирует действие — интеграл от функции Лагранжа по времени. Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией.
Метри́ческий те́нзор, или ме́трика, — симметричное тензорное поле ранга (0,2) на гладком многообразии, посредством которого задаётся скалярное произведение векторов в касательном пространстве. Иначе говоря, метрический тензор задаёт билинейную форму на касательном пространстве к этой точке, обладающую свойствами скалярного произведения и гладко зависящую от точки.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.
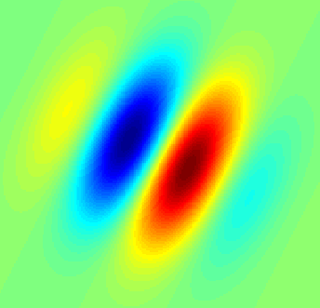
Фильтр Габора — линейный электронный фильтр, импульсная переходная характеристика которого определяется в виде гармонической функции, помноженной на гауссиан. При цифровой обработке изображений этот фильтр применяется для распознавания границ объектов.
А́том водоро́да — физико-химическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра, как правило, входит протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон образует электронную оболочку; наибольшая вероятность обнаружения электрона в единичном объёме наблюдается для центра атома. Интегрирование по сферическому слою показывает, что наибольшая вероятность обнаружения электрона в единичном слое соответствует среднему радиусу, равному боровскому радиусу  ангстрема.
ангстрема.
Криволине́йная систе́ма координа́т, или криволине́йные координа́ты, — система координат в евклидовом (аффинном) пространстве, или в области, содержащейся в нём. Криволинейные координаты не противопоставляются прямолинейным, последние являются частным случаем первых. Применяются обычно на плоскости (n=2) и в пространстве (n=3); число координат равно размерности пространства n. Наиболее известным примером криволинейной системы координат являются полярные координаты на плоскости.
Парадо́кс Кле́йна в графе́не — прохождение любых потенциальных барьеров без обратного рассеяния под прямым углом. Эффект связан с тем, что спектр носителей тока в графене линейный и квазичастицы подчиняются уравнению Дирака для графена. Эффект предсказан теоретически в 2006 году для прямоугольного барьера.
Здесь приведён список векторных дифференциальных операторов в различных системах координат.
Реше́ние Ке́рра — Нью́мена — точное решение уравнений Эйнштейна, описывающее невозмущённую электрически заряженную вращающуюся чёрную дыру без космологического члена. Астрофизическая значимость решения неясна, так как предполагается, что встречающиеся в природе коллапсары не могут быть существенно электрически заряжены.
Статическая изотропная метрика — это метрика, определяющая статическое изотропное гравитационное поле. Частным случаем этой метрики является метрика Шварцшильда, на случай пустого пространства-времени.

Фотоны, которые мигрируют в биологических тканях могут быть описаны при помощи численного моделирования методом Монте Карло или аналитическим уравнением переноса излучения (УПИ). Однако, УПИ трудно решается без применения упрощений (приближений). Стандартным методом упрощения УПИ является диффузионное приближение. Общее решение уравнения диффузии для фотонов получается быстрее, но менее точно чем методом Монте Карло.
Обобщённые координаты — переменные состояния системы, описывающие конфигурацию динамической системы относительно некоторой эталонной конфигурации в аналитической механике, а конкретно исследовании динамики твёрдых тел в системе многих тел. Эти переменные должны однозначно определять конфигурацию системы относительно эталонной конфигурации. Обобщённые скорости — производные по времени обобщённых координат системы.
Ме́тод Га́усса в небесной механике и астродинамике используется для первоначального определения параметров орбиты небесного тела по трём наблюдениям.
Диполя́рная, или дипо́льная, систе́ма координа́т — трёхмерная криволинейная ортогональная система координат, основанная на точечном (центральном) диполе, точнее, на его инвариантах преобразования координат.
Формула Сантало́ — следствие теоремы Лиувилля о сохранении фазового объёма применяемая для интегрирования функций заданных на расслоении единичных сфер риманова многообразия. А именно она даёт возможность сначала интегрировать по каждой геодезической отдельно, а затем по пространству всех геодезических.

![{\displaystyle h\colon [-1,1]\to (-1,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba1591adb5a4700221b75086a48fc5d979ad5e2a)



















