
Шестиуго́льный парке́т или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Сферический многогранник или сферическая мозаика — это тa мозаика на сфере, в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.
Теорема Штайница — это комбинаторное описание неориентированных графов, образованных рёбрами и вершинами трёхмерного выпуклого многогранника — они в точности являются (простыми) вершинно 3-связными планарными графами. То есть любой выпуклый многогранник образует 3-связный планарный граф, и любой 3-связный планарный граф может быть представлен как выпуклый многогранник. По этой причине 3-связные планарные графы называют также полиэдральными.

Пространственный многоугольник — многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется.

Звёздчатый октаэдр, или stella octangula, — единственная звёздчатая форма октаэдра. Латинским именем stella octangula многогранник назвал Кеплер в 1609, хотя он был известен более ранним геометрам. Так, он изображён в труде Пачоли De Divina Proportione, 1509.
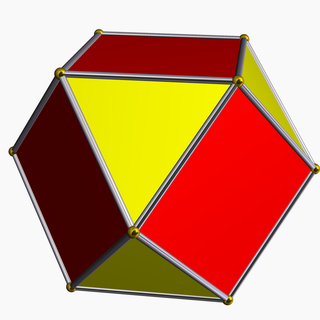
В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек. Получающийся многогранник будет ограничен фасетами вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Так, например, r{4,3} — спрямлённый куб, т.е. кубооктаэдр.

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.
Правильный косой многогранник — это обобщение множества правильных многогранников, которое включает возможность непланарных граней или вершинных фигур. Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани.

Тороидальный многогранник — это многогранник, который является также тороидом, имеющий топологический род, g, равный 1 или выше.

Диэдр — вид многогранника, состоящего из двух многоугольных граней, имеющих общий набор рёбер. В трёхмерном евклидовом пространстве он является вырожденным, если его грани плоские, в то время как в трёхмерном сферическом пространстве диэдр с плоскими гранями может рассматриваться как линза, примером которой является фундаментальная область линзового пространства L(p,q).

Четырёхмерный многогранник — многогранник в четырёхмерном пространстве. Многогранник является связанной замкнутой фигурой, состоящей из многогранных элементов меньшей размерности — вершин, рёбер, граней (многоугольников) и ячеек. Каждая грань принадлежит ровно двум ячейкам.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

В математике абстрактный многогранник, неформально говоря, это структура, которая учитывает только комбинаторные свойства традиционных многогранников и игнорирует много других их свойств, таких как углы, длины рёбер и т. д. При этом не требуется наличие какого-либо содержащего многогранник пространства, такого как евклидово пространство. Абстрактная формулировка реализует комбинаторные свойства как частично упорядоченное множество («посет»).

3-3 дуопризма или треугольная дуопризма, наименьшая из p-q дуопризм, это четырёхмерный многогранник, получающийся прямым произведением двух треугольников.
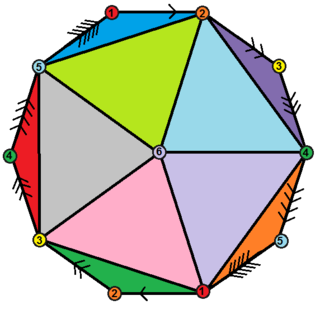
Полуикосаэдр — абстрактный правильный многогранник, содержащий половину граней правильного икосаэдра. Он может быть реализован как проективный многогранник, который можно представить себе путём построения проективной плоскости как полусферы, противоположные точки которой вдоль границы соединены и делят полусферу на три равные части.
Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.

Вещественная проективная плоскость является примером компактного неориентированного двумерного многообразия, другими словами, односторонней поверхности. Проективную плоскость невозможно вложить в обычное трёхмерное пространство без самопересечения. Основная область применения этой плоскости — геометрия, поскольку основное построение вещественной проективной плоскости — пространство прямых в R3, проходящих через начало координат.

Правильная карта — это симметричное замощение замкнутой поверхности. Более точно, правильная карта — это разложение двумерного многообразия на топологические диски, так что каждый флаг может быть переведён в любой другой флаг преобразованием симметрии разложения. Правильные карты являются в некотором смысле топологическим обобщением правильных многогранников. Теория карт и их классификация связана с теориями римановых поверхностей, геометрии Лобачевского и теории Галуа. Правильные карты классифицируются по их роду ориентируемости соответствующей поверхности, по основному графу или автоморфизму группы.



















