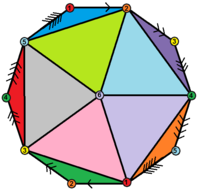
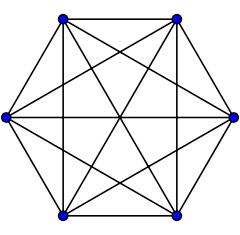
Окта́эдр — многогранник с восемью гранями.

Шестиуго́льный парке́т или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Сферический многогранник или сферическая мозаика — это тa мозаика на сфере, в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.

Усечение — операция в пространстве любой размерности, которая отсекает вершины многогранника и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.

Линк вершины многогранника или вершинная фигура — многогранник на единицу меньшей размерности, который получается в сечении исходного многогранника плоскостью, срезающей одну вершину. В частности линк вершины содержит информацию о порядке следования граней многогранника вокруг одной вершины.

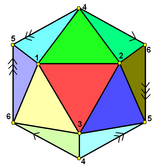
Звёздчатый октаэдр, или stella octangula, — единственная звёздчатая форма октаэдра. Латинским именем stella octangula многогранник назвал Кеплер в 1609, хотя он был известен более ранним геометрам. Так, он изображён в труде Пачоли De Divina Proportione, 1509.
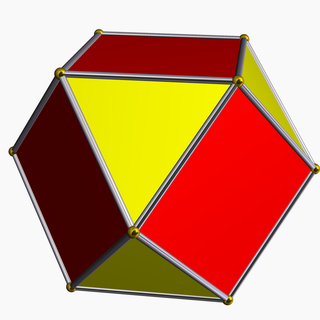
В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек. Получающийся многогранник будет ограничен фасетами вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Так, например, r{4,3} — спрямлённый куб, т.е. кубооктаэдр.

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Тороидальный многогранник — это многогранник, который является также тороидом, имеющий топологический род, g, равный 1 или выше.

Диэдр — вид многогранника, состоящего из двух многоугольных граней, имеющих общий набор рёбер. В трёхмерном евклидовом пространстве он является вырожденным, если его грани плоские, в то время как в трёхмерном сферическом пространстве диэдр с плоскими гранями может рассматриваться как линза, примером которой является фундаментальная область линзового пространства L(p,q).

Четырёхмерный многогранник — многогранник в четырёхмерном пространстве. Многогранник является связанной замкнутой фигурой, состоящей из многогранных элементов меньшей размерности — вершин, рёбер, граней (многоугольников) и ячеек. Каждая грань принадлежит ровно двум ячейкам.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

В математике абстрактный многогранник, неформально говоря, это структура, которая учитывает только комбинаторные свойства традиционных многогранников и игнорирует много других их свойств, таких как углы, длины рёбер и т. д. При этом не требуется наличие какого-либо содержащего многогранник пространства, такого как евклидово пространство. Абстрактная формулировка реализует комбинаторные свойства как частично упорядоченное множество («посет»).

В математике 11-ячейник — это самодвойственный абстрактный правильный 4-мерный многогранник. Его 11 ячеек являются полуикосаэдрами. Он имеет 11 вершин, 55 рёбер и 55 граней. Его группой симметрии является проективная специальная линейная группа L2(11), так что многогранник имеет 660 симметрий. Он имеет символ Шлефли {3,5,3}.

3-3 дуопризма или треугольная дуопризма, наименьшая из p-q дуопризм, это четырёхмерный многогранник, получающийся прямым произведением двух треугольников.
Комплексный многогранник — это обобщение многогранника в вещественном пространстве на аналогичную структуру в комплексном гильбертовом пространстве, где к каждой вещественной размерности добавляется мнимая.
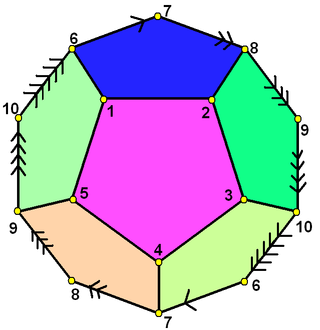
Полудодекаэдр — абстрактный правильный многогранник, содержащий половину граней правильного додекаэдра. Данный многогранник можно представить в виде проективного многогранника, который можно изобразить при построении проективной плоскости в виде полусферы, где противоположные точки вдоль границы соединены и разбивают полусферу на три равные части.

Правильная карта — это симметричное замощение замкнутой поверхности. Более точно, правильная карта — это разложение двумерного многообразия на топологические диски, так что каждый флаг может быть переведён в любой другой флаг преобразованием симметрии разложения. Правильные карты являются в некотором смысле топологическим обобщением правильных многогранников. Теория карт и их классификация связана с теориями римановых поверхностей, геометрии Лобачевского и теории Галуа. Правильные карты классифицируются по их роду ориентируемости соответствующей поверхности, по основному графу или автоморфизму группы.