Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Пара́бола — плоская кривая, один из типов конических сечений.

Циссоида Диокла — плоская алгебраическая кривая третьего порядка. В декартовой системе координат, где ось абсцисс направлена по  , а ось ординат по
, а ось ординат по  , на отрезке
, на отрезке  , как на диаметре строится вспомогательная окружность. В точке
, как на диаметре строится вспомогательная окружность. В точке  проводится касательная
проводится касательная  . Из точки
. Из точки  проводится произвольная прямая
проводится произвольная прямая  , которая пересекает окружность в точке
, которая пересекает окружность в точке  и касательную в точке
и касательную в точке  . От точки
. От точки  , в направлении точки
, в направлении точки  , откладывается отрезок
, откладывается отрезок  , длина которого равна длине отрезка
, длина которого равна длине отрезка  . При вращении линии
. При вращении линии  вокруг точки
вокруг точки  , точка
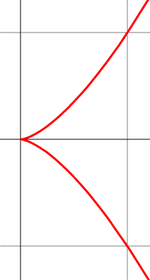
, точка  описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.
описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.

Касп, или точка возврата, — особая точка, в которой кривая линия разделяется на две ветви, имеющие в этой точке одинаковый направляющий вектор. То есть ветви в данной точке имеют общую касательную, и движение вдоль них из данной точки изначально происходит в одном и том же направлении.
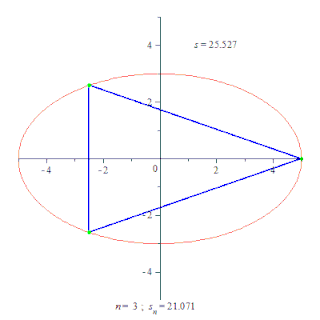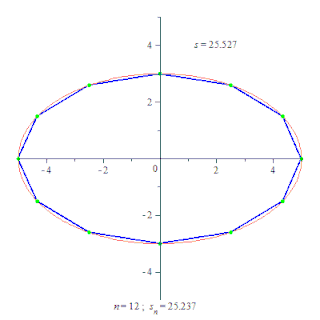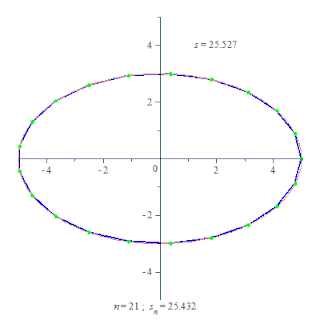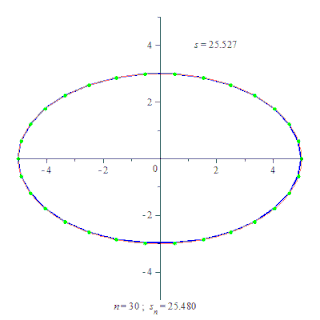
Длина́ криво́й — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой.

Поде́ра кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривой.
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида


Алгебраическая геометрия — раздел математики, который объединяет алгебру и геометрию. Главным предметом изучения классической алгебраической геометрии, а также в широком смысле и современной алгебраической геометрии, являются множества решений систем алгебраических уравнений. Современная алгебраическая геометрия во многом основана на методах общей алгебры для решения задач, возникающих в геометрии.

Алгебраическая кривая, или плоская алгебраическая кривая, — это геометрическое место (множество) точек на плоскости (O;x,y), которое определяется как множество нулей многочлена от двух переменных. Степенью (или порядком) n этой кривой называется степень этого многочлена. Алгебраические кривые степеней n = 1, 2, 3, …, 8 кратко называются прямыми, кониками, кубиками, квартиками, пентиками, секстиками, септиками, октиками соответственно. Например, единичная окружность — это алгебраическая кривая степени 2 (коника), так как она задаётся уравнением x2 + y2 − 1 = 0.
Менехм — древнегреческий математик, ученик Евдокса, член Афинской Академии Платона, брат математика Динострата. Упоминается у античных авторов как первый исследователь конических сечений и в связи с попытками решить проблему удвоения куба.
Пара́бола:
- Парабола — геометрическое место точек, равноудалённых от данной прямой и данной точки.
- Кубическая парабола — числовая функция, задаваемая многочленом третьей степени.
- Полукубическая парабола — плоская алгебраическая кривая.
- Парабола безопасности — огибающая параболических траекторий снарядов, выпущенных из определенной точки с заданной скоростью под разными углами к горизонту в фиксированной вертикальной плоскости.
- Парабола в литературе — близкий к притче рассказ иносказательного характера.

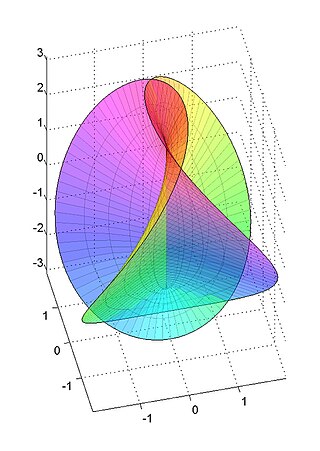
Ла́сточкин хвост — нерегулярная поверхность в трёхмерном пространстве, определить которую можно несколькими эквивалентными способами.

Алгебраическое многообразие — центральный объект изучения алгебраической геометрии. Классическое определение алгебраического многообразия — множество решений системы алгебраических уравнений над действительными или комплексными числами. Современные определения обобщают его различными способами, но стараются сохранить геометрическую интуицию, соответствующую этому определению.

Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.
Особая точка кривой — точка, в окрестности которой не существует гладкой параметризации. Точное определение зависит от типа изучаемой кривой.

Офиури́да — плоская алгебраическая кривая 3-го порядка.

«Геометрия» — труд Рене Декарта, опубликованный в Лейдене (Голландия) в 1637 году в качестве третьего приложения к философскому трактату Декарта «Рассуждение о методе». Число страниц: 106. Имя автора в первом издании не было указано. Это единственное сочинение Декарта, полностью посвящённое математике; оно рассматривалось автором как образец применения его общих методов. После 1637 года «Геометрия» издавалась отдельно от «Рассуждения о методе».
Теорема Безу — утверждение в алгебраической геометрии, описывающее число общих точек, или точек пересечения, двух плоских алгебраических кривых, не имеющих общей компоненты. Теорема утверждает, что число общих точек таких кривых не превосходит произведения их степеней, и имеет место равенство, если учитывать бесконечно удалённые точки и точки с комплексными координатами, и если точки считаются с кратностями, равными индексам пересечения.
Поверхность Хеннеберга — неориентируемая минимальная поверхность, названная именем немецкого математика Лебрехта Хенненберга.