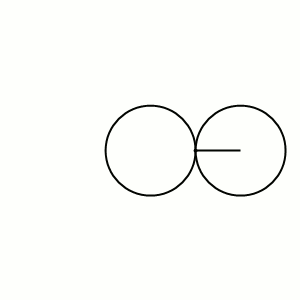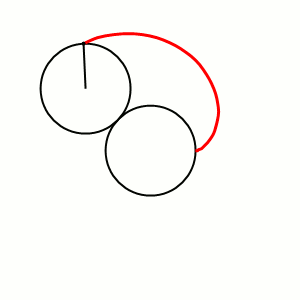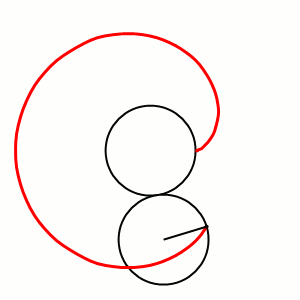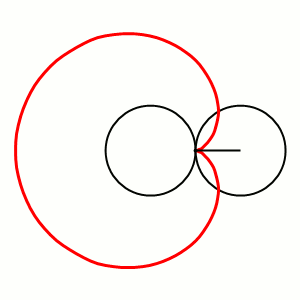Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Центр масс — геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого. Радиус-вектор данной точки задаётся формулой

Моме́нт и́мпульса — векторная физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение.

Циссоида Диокла — плоская алгебраическая кривая третьего порядка. В декартовой системе координат, где ось абсцисс направлена по  , а ось ординат по
, а ось ординат по  , на отрезке
, на отрезке  , как на диаметре строится вспомогательная окружность. В точке
, как на диаметре строится вспомогательная окружность. В точке  проводится касательная
проводится касательная  . Из точки
. Из точки  проводится произвольная прямая
проводится произвольная прямая  , которая пересекает окружность в точке
, которая пересекает окружность в точке  и касательную в точке
и касательную в точке  . От точки
. От точки  , в направлении точки
, в направлении точки  , откладывается отрезок
, откладывается отрезок  , длина которого равна длине отрезка
, длина которого равна длине отрезка  . При вращении линии
. При вращении линии  вокруг точки
вокруг точки  , точка
, точка  описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.
описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.
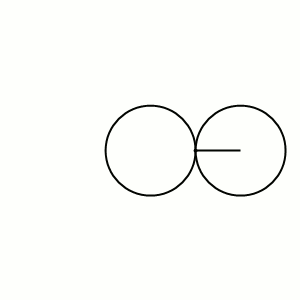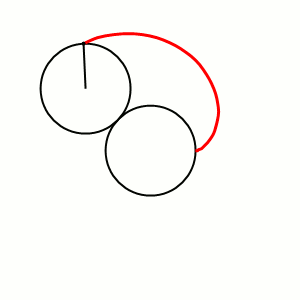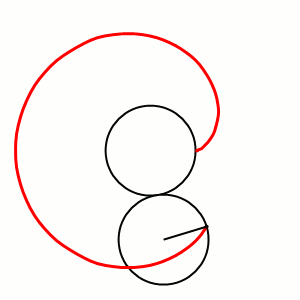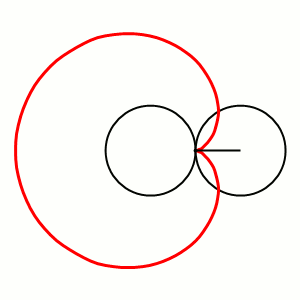
Кардио́ида, или сердцеви́дная крива́я — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.
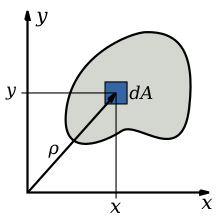
Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения, но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.
Функция Вигнера была введена Вигнером в 1932 году для изучения квантовых поправок к классической статистической механике. Целью было заменить волновую функцию, которая появляется в уравнении Шрёдингера на функцию распределения вероятности в фазовом пространстве. Она была независимо выведена Вейлем в 1931 году как символ матрицы плотности теории представлений в математике. Функция Вигнера применяется в статистической механике, квантовой химии, квантовой оптике, классической оптике и анализе сигналов в различных областях, таких как электроника, сейсмология, акустика, биология. При анализе сигналов используются названия преобразование Вигнера — Вилла и распределение Вигнера — Вилла.

Торсио́н — стержень из упругого материала, имеющий относительно небольшую крутильную жёсткость, высокую упругость и работающий на кручение.
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое описывает
- электростатическое поле,
- гравитационное поле,
- стационарное поле температуры,
- поле давления,
- поле потенциала скорости в гидродинамике.
Вселе́нная Фри́дмана — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга вокруг его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Рассе́яние части́ц — изменение направления движения частиц в результате столкновений с другими частицами.
Изгиб — в сопротивлении материалов вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев, изменение кривизны/искривление срединной поверхности пластины или оболочки. Изгиб связан с возникновением в поперечных сечениях бруса или оболочки изгибающих моментов. Прямой изгиб балки возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.

Квадратри́са — плоская трансцендентная кривая, определяемая кинематически. Была предложена в античные времена для решения задач квадратуры круга и трисекции угла. Квадратриса стала первой в математике трансцендентной кривой.
Векторными сферическими гармониками являются векторные функции, преобразующиеся при вращениях системы координат так же, как скалярные сферические функции с теми же индексами, или определенные линейные комбинации таких функций.
Мультипольное излучение — излучение, обусловленное изменением во времени мультипольных моментов системы. Используется для описания электромагнитного или гравитационного излучения от изменяющегося во времени (нестационарного) распределения удалённых источников. Мультипольное разложение применяется к физическим явлениям, которые происходят на разных масштабах — от гравитационных волн из-за столкновения галактик до гамма-излучения в результате радиоактивного распада. Мультипольное излучение анализируется способами, схожими с применяемыми для мультипольного разложения полей от стационарных источников. Однако есть важные отличия, поскольку поля мультипольного излучения ведут себя несколько иначе полей от стационарных источников. Эта статья в первую очередь касается электромагнитного мультипольного излучения, хотя гравитационные волны рассматриваются аналогично.
Преобразование Фурье на группах — обобщение дискретного преобразования Фурье от циклических к локально компактным абелевым группам или произвольным компактным группам.