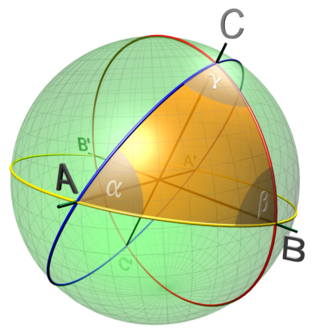
Полярный треугольник

Поля́рный треуго́льник — понятие сферической тригонометрии[1].
Полярный треугольник для сферического треугольника — новый сферический треугольник , вершины которого суть полюсы больших окружностей, содержащих стороны исходного треугольника , причём эти полюсы лежат на тех же полусферах, что и исходный треугольник (см. рисунок справа с красным полярным треугольником)[2][3][4].
Определения
Определение 1. Полярный треугольник для сферического треугольника — новый сферический треугольник , вершины которого суть полюсы больших окружностей, содержащих стороны исходного треугольника , причём эти полюсы лежат на тех же полусферах, что и исходный треугольник (см. рисунок в начале статьи с красным полярным треугольником)[3][2].
Это определение можно использовать для построения полярного треугольника[2].
Построение полярного треугольника 1. Пусть дан произвольный сферический треугольник . Строим точки , и как полюсы больших окружностей, на которых лежат соответственно стороны , и исходного треугольника, причём эти полюсы лежат на тех же полусферах, что и исходный треугольник. Соединив построенные точки короткими дугами больших окружностей, получим полярный сферический треугольник [2].

В определении 1 используются вершины нового полярного треугольника и стороны исходного. Поскольку эти треугольники взаимно полярны, иногда ещё используют определение полярного треугольника, в котором используются, наоборот, вершины исходного треугольника и стороны полярного[4].
Определение 2. Полярный треугольник для сферического треугольника — новый сферический треугольник , стороны которого лежат на больших окружностях, относительно которых вершины исходного треугольника суть полюсы, причём эти полюсы лежат на тех же полусферах, что и полярный треугольник (см. рисунок справа с красным полярным треугольником)[4].
И это определение можно использовать для построения полярного треугольника[4].
Построение полярного треугольника 2. Пусть дан произвольный сферический треугольник . Проведём поляры его вершин — большие окружности, получим восемь сферических треугольников. Полярным треугольником будет тот из восьми треугольников, стороны которого , и находятся с точками соответственно , и на одной полусфере относительно поляр этих точек[4].
Свойства
Полярные треугольники обладают свойством взаимности[5]: если сферический треугольник ABC полярен относительно сферического треугольника LMN, то и сферический треугольник LMN полярен относительно сферического треугольника ABC. Углы одного из полярных друг относительно друга треугольников дополняют стороны другого треугольника до развёрнутого угла. Таким образом, каждая теорема или формула, относящаяся к сторонам и углам треугольника, может быть преобразована в двойственную теорему или формулу об углах и сторонах полярного треугольника.
Если все стороны сферического треугольника меньше прямого угла, он будет лежать внутри полярного треугольника. Если все стороны сферического треугольника больше прямого угла, он будет сам содержать полярный треугольник. Если хотя бы одна сторона сферического треугольника меньше или равна прямому углу, тогда как остальные — больше, то он будет пересекаться с полярным треугольником[6]. Сферический треугольник, все стороны которого равны прямому углу, будет полярен самому себе.
История
Самый ранний пример применения полярного треугольника содержится в «Трактате о познании небесных дуг» Абу Насра ибн Ирака. Ибн Ирак вводит полярный треугольник при вычислении сторон данного сферического треугольника по трём его углам. Аналогичным методом пользовались впоследствии ал-Джайяни в «Книге о неизвестных дугах сферы» и Насир ад-Дин ат-Туси в «Трактате о полном четырёхстороннике».
Понятие «полярный треугольник» в Европе распространилось в 18 веке благодаря В.Снеллиусу[1], который вывел его основные свойства[7].
Примечания
- ↑ 1 2 Степанов Н. Н. Сферическая тригонометрия, 1948, § 5. Полярный сферический треугольник и его свойства, с. 14.
- ↑ 1 2 3 4 Адамар Ж. Элементарная геометрия. Часть вторая. Стереометрия, 1952, 395—396. Пополнительные трёхгранные углы. Полярные сферические треугольники, с. 64—65.
- ↑ 1 2 Розенфельд Б. А. Основные понятия сферической геометрии и тригонометрии, 1963, 2.2. Полярные треугольники, с. 530—531.
- ↑ 1 2 3 4 5 Степанов Н. Н. Сферическая тригонометрия, 1948, § 5. Полярный сферический треугольник и его свойства, с. 12.
- ↑ Weisstein Eric W. Polar Triangle, 2024.
- ↑ Степанов Н.Н. Полярный сферический треугольник и его свойства // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 12—14. — 154 с.
- ↑ Rouse Ball W. W. A short account of the history of mathematics, 1960, Snell, p. 210.
Источники
- Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. Пособие для учителей средней школы. Изд. 2-е с прил. составленных проф. Д. И. Перепёлкиным решений всех помещённых в тексте задач / Пер. с 7-го изд. под ред. проф. Д. И. Перепёлкина. М.: Учпедгиз, 1952. 760 с., ил.
- Розенфельд Б. А. Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 518—557.
- Степанов Н. Н. Сферическая тригонометрия. 2-е изд. М.—Л.: ОГИЗ. Государственное издательство технико-теоретической литературы, 1948. 154 с., ил.
- Rouse Ball W. W.[англ.] A short account of the history of mathematics. 4th edition. New York: Dover Publications, Inc, 1960. 439 p.
- Weisstein Eric W. Polar Triangle // Wolfram MathWorld Архивная копия от 25 сентября 2024 на Wayback Machine
Литература
- Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.