Порождающее множество группы
Порождающее множество группы — это такое её подмножество, что каждый её элемент может быть представлен в виде конечного произведения элементов из этого подмножества и их обратных. Также используются термины множество образующих[1] и система образующих.
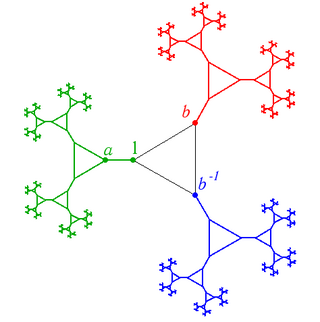
Одна и та же группа может иметь много разных порождающих множеств. Указание порождающего множества позволяет ввести на группе структуру графа Кэли. Кроме того, группы можно задавать, указывая порождающие множества и соотношения между ними.
Определение
Пусть — подмножество группы . Подгруппой, порождённой множеством , называется множество всех элементов, которые могут быть представлены в виде конечного произведения элементов из и их обратных. (другими словами, в G нет хотя бы одной собственной подгруппы, содержащей S) Если пусто, то, по-определению, является тривиальной подгруппой, состоящей только из нейтрального элемента.
Если , то говорят, что порождает группу . При этом множество называется порождающим, а его элементы — образующими или генераторами (от англ. generators) группы.
Любая группа имеет хотя бы одно порождающее множество: .
Если в группе можно выбрать конечное множество образующих, то её называют конечно порождённой. Мощность наименьшего порождающего множества группы называется её рангом.
Например, циклические группы — это в точности группы ранга один.
Замечания
- Множество совпадает с пересечением всех подгрупп группы , содержащих , и является наименьшей подгруппой в , содержащей .
- Если состоит только из одного элемента , обычно пишут вместо . В таком случае — циклическая подгруппа, состоящая из всех степеней элемента .
Порождающие полугруппы и моноида
Для случая, когда является полугруппой или моноидом, тоже можно ввести аналогичное понятие порождающего множества: порождает как полугруппу или моноид, если является минимальной полугруппой или минимальным моноидом соответственно, содержащим .
Такое определение тоже можно изложить на языке представимости элемента в виде комбинации. Для полугруппы можно сказать, что является порождающим множеством, если каждый элемент можно представить как конечное произведение элементов из . Для моноида можно сказать, что является порождающим множеством, если каждый элемент , кроме нейтрального, можно представить как конечное произведение элементов из .
Из-за разницы определений одно и то же множество может быть порождающим в одном смысле, но не быть в другом. Например, для моноида неотрицательных целых чисел порождающим множеством будет , но для полугруппы уже не является порождающим множеством, так как 0 нельзя представить в виде суммы единиц. Аналогично, для как группы является порождающим множеством, а для моноида — нет, так как в определении порождающего множества для моноида не включено взятие обратных.
Примечания
- ↑ Ленг, 1968, с. 23.
Литература
- Ленг С. Алгебра. — М.: Мир, 1968. — 564 с.
- Курош А. Г. Теория групп. — М.: Наука, 1967. — 648 с.
- Введение в алгебру часть 1 Основы алгебры 149 с.