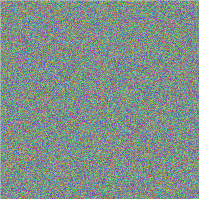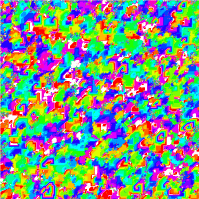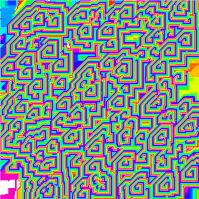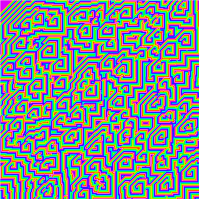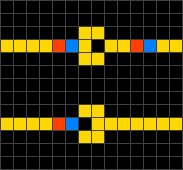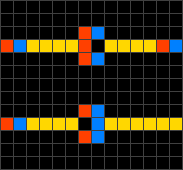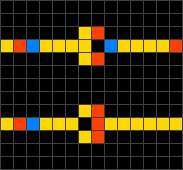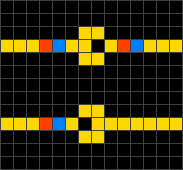Правило 184

Правило 184 (англ. Rule 184) — элементарный клеточный автомат, то есть одномерный клеточный автомат с двумя состояниями (0 и 1).
Определение
Состояние клеточного автомата задаётся линейным массивом клеток, каждая из которых содержит двоичное значение (0 или 1). На каждом шаге эволюции правило (в данном случае — правило 184) применяется одновременно к каждой из ячеек массива и определяет её новое состояние следующим образом:
| Текущая окрестность клетки | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| Новое состояние клетки | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
Запись в этой таблице определяет новое состояние каждой клетки в зависимости от предыдущего состояния этой клетки и двух её соседей слева и справа.
Название правила представляет собой код Вольфрама, описывающий приведённую таблицу: нижняя строка таблицы (10111000) при переводе из двоичной системы счисления в десятичную даёт 8 + 16 + 32 + 128 = 184.
Правило 184 можно описать на интуитивном уровне несколькими различными способами:
- На каждом шаге пары состояний вида 10 изменяются на пары вида 01. На основании этого описания Краг и Спон (1984) называют правило 184 детерминированной версией «кинетической модели Изинга с асимметричной спин-обменной динамикой».
- На каждом шаге клетка в состоянии 1, справа от которой находится клетка в состоянии 0 («свободное пространство»), перемещается вправо, освобождая занятое пространство. Это описание соответствует применению, связанному с моделированием транспортных потоков.
- Если клетка находится в состоянии 0, то её новое состояние берётся из ячейки слева от неё. В противном случае, её состояние берётся из ячейки справа от неё. Иными словами, каждая ячейка может быть реализована с помощью мультиплексора и по своему действию напоминает вентиль Фредкина[1].
Эволюция
Из описания правил можно вывести два свойства, связанных с динамикой правил. Во-первых, в течение эволюции конечного множества клеток по правилу 184 в автомате с периодическими граничными условиями[англ.], число клеток в состоянии 1 (и 0) остаётся неизменным. В массиве клеток бесконечной длины, если плотность распределения клеток в состоянии 1 определена, она также остаётся неизменной в течение эволюции[2].
Во-вторых, хотя правило 184 не является симметричным относительно перемены левого и правого направлений, оно обладает следующей симметрией: перемена левого и правого направлений с одновременной переменой ролей 1 и 0 приводит к тем же правилам эволюции.
В автомате с правилом 184 образцы (последовательности состояний клеток) обычно быстро стабилизируются, приводя к последовательности состояний, движущейся в одном из двух направлений[3].
- Если начальная плотность «единиц» меньше 50 %, в результате эволюции возникают движущиеся вправо кластеры «единиц», разделённых «нулями»; кластеры разделены блоками «нулей».
- Если начальная плотность больше 50 %, образец эволюционирует в движущиеся влево кластеры «нулей», разделённых «единицами»; кластеры разделены группами «единиц».
- Если начальная плотность равна 50 %, образец более медленно стабилизируется в последовательность чередующихся «единиц» и «нулей», которую можно с равным успехом считать движущейся влево или вправо.
Правило 184 в качестве модели
Правило 184 позволяет решить задачу классификации плотности[англ.] и описать несколько на первый взгляд разных систем частиц:
- Правило 184 может быть использовано в качестве простой модели транспортного потока на однополосном шоссе и лежит в основе многих микроскопических моделей транспортного потока[англ.]. Частицы, обозначающие транспортные средства, движутся в одном направлении, останавливаются и начинают движение в зависимости от «состояния» автомобилей прямо перед ними. Количество частиц в течение симуляции остаётся неизменным. В cвязи с этим применением правило 184 также называют «дорожным правилом»[4].
- В физике аэрозолей правило 184 применяется для моделирования осаждения[англ.] частиц на нерегулярную поверхность, где на очередном шаге симуляции каждый локальный минимум поверхности заполняется частицей. В течение симуляции число частиц возрастает; помещённая частица не перемещается.
- Автомат с правилом 184 можно рассматривать в контексте баллистической аннигиляции, как систему частиц, движущихся влево и вправо в одномерной среде. Когда две частицы сталкиваются, они аннигилируют друг с другом, так что на каждом шаге число частиц остается неизменным или уменьшается.
Кажущиеся противоречия между этими описаниями разрешаются различием способов установления взаимосвязи между свойствами клеточного автомата и элементами задачи.
Первые исследования правила 184, по-видимому, были выполнены Ли (1987) и Крагом и Споном (1988). В частности, Краг и Спон описали все три типа систем частиц, моделируемых с помощью правила 184[5].
Примечания
- ↑ Li (1992).
- ↑ Boccara и Fukś (1998) и Moreira (2003) исследовали более общий класс клеточных автоматов с аналогичными законами сохранения.
- ↑ Li (1987).
- ↑ См., напр., Fukś (1997).
- ↑ Во многих поздних работах при упоминании правила 184 приводятся ссылки на ранние статьи Стивена Вольфрама, в которых, однако, рассматривались лишь автоматы, симметричные относительно перемены левого и правого направлений и, следовательно, не рассматривалось правило 184.
Литература
- Fukś, Henryk. Solution of the density classification problem with two similar cellular automata rules (англ.) // Physical Review E : journal. — 1997. — Vol. 55, no. 3. — P. R2081—R2084. — doi:10.1103/PhysRevE.55.R2081. — .
- Fukś, Henryk; Boccara, Nino. Generalized deterministic traffic rules (неопр.) // Journal of Modern Physics C. — 1998. — Т. 9, № 1. — С. 1—12. — doi:10.1142/S0129183198000029. — . Архивировано 27 сентября 2007 года.
- Li, Wentian. Power spectra of regular languages and cellular automata (англ.) // Complex Systems : journal. — 1987. — Vol. 1. — P. 107—130. Архивировано 7 октября 2007 года.
- Li, Wentian. Phenomenology of nonlocal cellular automata (англ.) // Journal of Statistical Physics[англ.] : journal. — 1992. — Vol. 68, no. 5—6. — P. 829—882. — doi:10.1007/BF01048877. — .
- Moreira, Andres. Universality and decidability of number-conserving cellular automata (англ.) // Theoretical Computer Science : journal. — 2003. — Vol. 292, no. 3. — P. 711—721. — doi:10.1016/S0304-3975(02)00065-8. — arXiv:nlin.CG/0306032.
Ссылки
- Правило 184 Архивная копия от 30 октября 2010 на Wayback Machine в атласе Стивена Вольфрама
- Java Simulator Архивная копия от 3 сентября 2010 на Wayback Machine (симуляция на замкнутом в кольцо массиве клеток, длина массива фиксирована, по умолчанию задано правило 184)