Игра «Жизнь» — клеточный автомат, придуманный английским математиком Джоном Конвеем в 1970 году. Это игра без игроков, в которой человек создаёт начальное состояние, а потом лишь наблюдает за её развитием. В игре можно создать процессы с полнотой по Тьюрингу, что позволяет реализовать любую машину Тьюринга.

Кле́точный автома́т — дискретная модель, изучаемая в математике, теории вычислимости, физике, теоретической биологии и микромеханике. Основой является пространство из прилегающих друг к другу клеток (ячеек), образующих решётку. Каждая клетка может находиться в одном из конечного множества состояний. Решётка может быть любой размерности, бесконечной или конечной, для решётки с конечными размерами часто предусматривается закольцованность при достижении предела (границы). Для каждой клетки определено множество клеток, называемых окрестностью. Например, окрестность фон Неймана ранга 2 включает все клетки на расстоянии не более 2 от текущей. Устанавливаются правила перехода клеток из одного состояния в другое. Обычно правила перехода одинаковы для всех клеток. Один шаг автомата подразумевает обход всех клеток и на основе данных о текущем состоянии клетки и её окрестности определение нового состояния клетки, которое будет у неё при следующем шаге. Перед стартом автомата оговаривается начальное состояние клеток, которое может устанавливаться целенаправленно или случайным образом.

Стивен Вольфрам — британский физик, математик, программист и писатель. Разработчик системы компьютерной алгебры Mathematica и системы извлечения знаний WolframAlpha.

Фронтальный клеточный автомат - специальный тип вычислительных алгоритмов, основанных на моделях клеточных автоматов.

Правило 184 — элементарный клеточный автомат, то есть одномерный клеточный автомат с двумя состояниями.
A New Kind of Science — популярная, отмеченная многими наградами и вызывающая разногласия в оценках книга Стивена Вольфрама, изданная в 2002 году. Она содержит эмпирическое и систематическое обсуждение таких вычислительных систем, как клеточный автомат. Вольфрам называет эти системы простыми программами и утверждает, что научная философия и методы, применимые для изучения простых программ, также являются применимыми и в других областях науки.
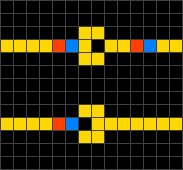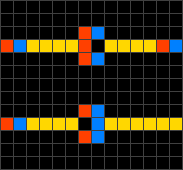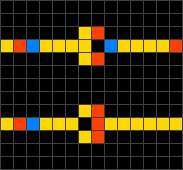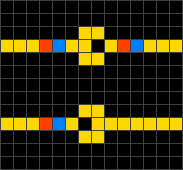
Wireworld — клеточный автомат, предложенный Брайаном Сильверманом в 1987 году, смоделированный в его программе Phantom Fish Tank. Автомат стал более известен после опубликования статьи в колонке «Computer Recreations» журнала Scientific American. Wireworld в особенности пригоден для симуляции электронных логических элементов, или «гейтов». Несмотря на простоту правил, Wireworld является полным по Тьюрингу.

Пра́вило 30 — элементарный клеточный автомат, то есть одномерный клеточный автомат с двумя состояниями, впервые описанный Стивеном Вольфрамом в 1983 году. Стивен Вольфрам говорит, что «это его самое любимое правило», и подробно описывает его в своей книге «A New Kind of Science». Из четырёх типов поведения, описанных в этой книге, Правило 30 обладает классом поведения III, показывая апериодическое, хаотическое поведение.
Сад Эде́ма — конфигурация в игре «Жизни» Конвея или другом клеточном автомате, которая не может появиться в результате эволюции, потому что не имеет предшественников. Термин «сад Эдема» был введён Джоном Тьюки ещё в 1950-х годах, задолго до появления «Жизни».

Правило 110 — один из вариантов элементарного клеточного автомата, в котором последовательность результатов преобразования образуют бинарную последовательность 01101110, что является двоичным представлением десятичного числа 110. Все элементарные клеточные автоматы представляют собой бесконечную ленту из последовательно размещённых клеток, которые могут иметь только два состояния и при этом будущее состояние клетки зависит от текущих значений трёх клеток — её самой и двух её ближайших соседей.
В математике негафибоначчиева система счисления — универсальный код, который кодирует ненулевые целые числа в двоичные кодовые слова. Обобщает фибоначчиеву систему счисления на все ненулевые целые числа. Все коды заканчиваются "11" и не имеют "11" в середине или начале слова. Коды для целых чисел от -11 до 11 приведены ниже.
xx негафибоначчиево представление негафибоначчиев код
-11 101000 0001011
-10 101001 1001011
-9 100010 0100011
-8 100000 0000011
-7 100001 1000011
-6 100100 0010011
-5 100101 1010011
-4 1010 01011
-3 1000 00011
-2 1001 10011
-1 10 011
0 0
1 1 11
2 100 0011
3 101 1011
4 10010 010011
5 10000 000011
6 10001 100011
7 10100 001011
8 10101 101011
9 1001010 01010011
10 1001000 00010011
11 1001001 10010011
Элементарный клеточный автомат — это клеточный автомат с одномерным массивом ячеек в форме бесконечной в обе стороны ленты, который имеет два возможных состояния ячеек и правило для определения состояния ячейки на следующем шаге, использующее только состояние ячейки и её двух соседей на текущем шаге. В целом такие автоматы являются одними из наиболее простых возможных клеточных автоматов, однако при некоторых правилах они показывают сложное поведение; так, использование правила 110 приводит к полному по Тьюрингу автомату.

Долгожи́тель — класс конфигураций клеточного автомата, в частности — игры «Жизнь» Конвея, которые состоят из небольшого числа живых ячеек в начальном состоянии, но стабилизируются только спустя много поколений. Под стабилизацией подразумевается распадение конфигурации на циклические и стабильные подконфигурации и удаляющиеся от точки старта космические корабли. Стабилизация для долгожителя обязательна, и это сужает круг применимости данного термина — во многих клеточных автоматах любая конфигурация либо быстро вымирает, либо растёт неограниченно.

Обратимый клеточный автомат — клеточный автомат, в котором каждое состояние имеет единственного предшественника. Таким образом, это регулярная решётка из ячеек, состояние каждой из которых берётся из конечного множества состояний, и правило для одновременного обновления состояний ячеек, исходя из состояний её соседей. Условие обратимости заключается в том, что предыдущее состояние любой ячейки может быть определено, зная обновлённые состояния всех ячеек решётки. После обращения времени получается другой обратимый клеточный автомат, возможно — с намного большими окрестностями, но также с правилом для определения будущего состояния ячейки, исходя из текущих состояний ей соседей.

«Криттеры» — блочный клеточный автомат, проявляющий поведение, схожее с игрой «Жизнь» Конвея; в частности, полон по Тьюрингу. Впервые описан Томмазо Тоффоли и Норманом Марголусом в 1987 году, как и некоторые другие обратимые клеточные автоматы.
Блочный клеточный автомат — класс клеточных автоматов, в которых решётка разбита на блоки, а функция перехода применяется к каждому блоку по отдельности. Блочные клеточные автоматы полезны для моделирования физических явлений, поскольку часто несложно выбрать функции перехода так, чтобы получившийся клеточный автомат был обратим и подчинялся выбранным законам сохранения.

Бильярдный компьютер — логическая модель для проведения обратимых вычислений, механический компьютер, основанный на законах движения Ньютона и предложенный в 1982 году Эдвардом Фредкиным и Томмазо Тоффоли.
«День и ночь» — клеточный автомат, модификация игры «Жизнь». Придуман и назван в 1997 году Нейтаном Томпсоном ; подробно исследован Дэвидом Беллом, который нашёл многие любопытные конфигурации и дал им имена.
«Жизнь без смерти» — клеточный автомат, модификация игры «Жизнь». Впервые описан в 1987 году Томмазо Тоффоли и Норманом Марголусом, которые дали ему название «Кляксы» — поскольку многие конфигураций автомата ведут себя подобно растекающемуся чернильному пятну. Известен также под названием «Хлопья».

«Семена́» — клеточный автомат, модификация игры «Жизнь». Придуман Брайаном Сильверманом, назван Миреком Вуйтовичем (Mirek Wójtowicz).