Практичное число

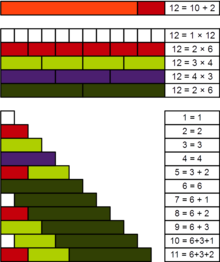
Практичное число или панаритмичное число^[1] — это положительное целое число n, такое что все меньшие положительные целые числа могут быть представлены в виде суммы различных делителей числа n. Например, 12 является практичным числом, поскольку все числа от 1 до 11 можно представить в виде суммы делителей 1, 2, 3, 4 и 6 этого числа — кроме самих делителей, мы имеем 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1 и 11 = 6 + 3 + 2.

Последовательность практичных чисел (последовательность A005153 в OEIS) начинается с

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

Практичные числа использовал Фибоначчи в своей книге Liber Abaci (1202) в связи с задачей представления рациональных чисел в виде египетских дробей. Фибоначчи не определял формально практичные числа, но он дал таблицу представления египетских дробей для дробей с практичными знаменателями^[2].

Название «практичное число» дал Шринивасан^[3]. Он заметил, что «разбиение денег, веса и других мер, использующие числа, такие как 4, 12, 16, 20 и 28, которые обычно так неудобны, что заслуживают замены на степени 10.» Он переоткрыл ряд теоретических свойств таких чисел и первым попытался классифицировать эти числа, а Стюарт^[4] и Серпинский^[5] завершили классификацию. Определение практичных чисел делает возможным определить, является ли число практичным путём просмотра разложения числа на простые множители. Любое чётное совершенное число и любая степень двойки является практичным числом.

Можно показать, что практичные числа аналогичны простым числам во многих отношениях^[6].

Исходное описание Шринивасана^[3] утверждает, что практичное число (кроме степени двойки) не может быть недостаточным числом. Если для практичного числа ${\displaystyle n}$ выписать упорядоченное множество делителей ${\displaystyle {d_{1},d_{2},...,d_{j}}}$, где ${\displaystyle d_{1}=1}$ и ${\displaystyle d_{j}=n}$, то утверждение Шринивасана можно выразить неравенством

${\displaystyle 2n\leqslant 1+\sum _{i=1}^{j}d_{i}}$.

Другими словами, упорядоченная последовательность всех делителей ${\displaystyle {d_{1}<d_{2}<...<d_{j}}}$ практичного числа должна быть полной подпоследовательностью.

Это определение расширили и завершили Стюарт^[4] и Серпинский^[5], которые показали, что определение, является ли число практичным, определяется его разложением на простые делители. Положительное целое число, большее единицы с разложением ${\displaystyle n=p_{1}^{\alpha _{1}}...p_{k}^{\alpha _{k}}}$ (с сортировкой простых делителей по возрастанию ${\displaystyle p_{1}<p_{2}<\dots <p_{k}}$), является практичным тогда и только тогда, когда каждый его простой делитель ${\displaystyle p_{i}}$ достаточно мал, чтобы ${\displaystyle p_{i}-1}$ имело представление в виде суммы меньших делителей. Чтобы это было верно, первое простое число ${\displaystyle p_{1}}$ должно быть равно 2, а для любого i от 2 до k, для каждого следующего простого числа ${\displaystyle p_{i}}$ должно выполняться неравенство

${\displaystyle p_{i}\leqslant 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},}$

где ${\displaystyle \sigma (x)}$ означает сумму делителей числа x. Например, ${\displaystyle 2\times 3^{2}\times 29\times 823=429606}$ является практичным, поскольку неравенство выполняется для каждого простого делителя: ${\displaystyle 3\leqslant \sigma (2)+1=4,29\leqslant \sigma (2\times 3^{2})+1=40}$ и ${\displaystyle 823\leqslant \sigma (2\times 3^{2}\times 29)+1=1171}$.

Условие, приведённое выше, является необходимым и достаточным. В одном направлении, это условие является необходимым, чтобы можно было представить ${\displaystyle p_{i}-1}$ в виде суммы делителей числа n, поскольку в случае нарушения неравенства сложение всех меньших делителей дало бы сумму, слишком маленькую, чтобы получить ${\displaystyle p_{i}-1}$. В другом направлении, условие является достаточным, что можно получить по индукции. Более строго, если разложение числа n удовлетворяет вышеприведённому условию, то любое число ${\displaystyle m\leqslant \sigma (n)}$ может быть представлено в виде суммы делителей числа n после следующих шагов^[4][5]:

• Пусть ${\displaystyle q=\min\{\lfloor m/p_{k}^{\alpha _{k}}\rfloor ,\sigma (n/p_{k}^{\alpha _{k}})\}}$, и пусть ${\displaystyle r=m-qp_{k}^{\sigma _{k}}}$.
• Учитывая, что можно показать по индукции, что ${\displaystyle q\leqslant \sigma (n/p_{k}^{\alpha _{k}})}$ и ${\displaystyle n/p_{k}^{\alpha _{k}}}$ являются практичными, мы можем найти представление q в виде суммы делителей ${\displaystyle n/p_{k}^{\alpha _{k}}}$.
• Учитывая, что можно показать по индукции, что ${\displaystyle r\leqslant \sigma (n)-p_{k}^{\alpha _{k}}\sigma (n/p_{k}^{\alpha _{k}})=\sigma (n/p_{k})}$ и ${\displaystyle n/p_{k}}$ являются практичными, мы можем найти представление r в виде суммы делителей ${\displaystyle n/p_{k}}$.
• Представление в виде делителей r, вместе с коэффициентом ${\displaystyle p_{k}^{\alpha _{k}}}$ для каждого делителя представления в виде делителей q, вместе образуют представление m в виде суммы делителей n.

• Единственное нечётное практичное число — 1, поскольку если n > 2 является нечётным числом, то 2 нельзя представить в виде суммы различных делителей числа n. Шринивасан^[3] заметил, что отличные от 1 и 2 практичные числа делятся на 4 и/или 6.
• Произведение двух практичных чисел является также практичным числом^[7]. Более сильное утверждение, наименьшее общее кратное любых двух практичных чисел, является также практичным числом. Эквивалентно, множество всех практичных чисел замкнуто по умножению.
• Из описания чисел Стюартом и Серпинским можно видеть, что в случае, когда n является практичным числом, а d является одним из его делителей, число n*d должно быть также практичным числом.
• В множестве всех практичных чисел существует множество простых практичных чисел. Простое практичное число — это либо практичное и свободное от квадратов число, либо практичное и при делении на любой его простой делитель, показатель которого в разложении больше 1, перестаёт быть практичным. Последовательность простых практичных чисел (последовательность A267124 в OEIS) начинается с

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

Несколько других достойных внимания множеств целых чисел состоят исключительно из практичных чисел:

• Из свойств, приведённых выше, для практичного числа n и одного из его делителей d (то есть, d|n) число n*d должно также быть практичным, так что помноженная на 6 любая степень числа 3 должна быть практичным числом, как и помноженная на 6 любая степень числа 2.
• Любая степень двойки является практичным числом ^[3]. Степень двойки тривиально удовлетворяет описанию практичных чисел в терминах разложения целых чисел — все простые числа в разложении числа, p₁, равны двум, что и требуется.
• Любое чётное совершенное число является также практичным числом^[3]. Это следует из результата Эйлера, что чётное совершенное число должно иметь вид ${\displaystyle 2^{n-1}(2^{n}-1)}$. Нечётная часть этого разложения равна сумме делителей чётной части, так что любое нечётный простой делитель такого числа должен быть не больше суммы делителей чётной части числа. Таким образом, это число должно удовлетворять описанию практичных чисел.
• Любой праймориал (произведение первых i простых для некоторого числа i) является практичным числом^[3]. Для первых двух праймориалов, двойки и шестёрки это ясно. Каждый последующий праймориал образуется умножением простого числа p_i на меньший праймориал, который делится как на двойку, так и на предыдущее простое число ${\displaystyle p_{i-1}}$. Согласно постулату Бертрана ${\displaystyle p_{i}<2p_{i-1}}$, так что каждый предшествующий простой делитель праймориала меньше, чем один из делителей предыдущего праймориала. По индукции, из этого следует, что любой праймориал удовлетворяет описанию практичных чисел. Поскольку праймориал по определению свободен от квадратов, он также является простым практичным числом.
• Обобщая праймориалы, любое число, являющееся произведением ненулевых степеней первых k простых чисел, должно быть практичным. В это множество попадают сверхсоставные числа Рамануджана (числа с количеством делителей, большим любого меньшего положительного числа), а также факториалы^[3].

Если n является практичным, то любое рациональное число вида m/n с m < n может быть представлен в виде суммы ${\displaystyle \sum {\tfrac {d_{i}}{n}}}$, где все d_i являются различными делителями числа n. Каждый член в этой сумме приводится к доле единицы, так что такая сумма даёт представление числа m/n в виде египетской дроби. Например,

${\displaystyle {\frac {13}{20}}={\frac {10}{20}}+{\frac {2}{20}}+{\frac {1}{20}}={\frac {1}{2}}+{\frac {1}{10}}+{\frac {1}{20}}.}$

Фибоначчи в своей книге 1202 года Liber Abaci^[2] приводит некоторые методы поиска представления рационального числа в виде египетской дроби. Из них первый метод заключается в проверке, не является ли число уже долей единицы, а второй метод заключается в представлении числителя в виде суммы делителей знаменателя, как описано выше. Это метод гарантирует успех только в случае, когда знаменатель является практичным числом. Фибоначчи привёл таблицы таких представлений для дробей, имеющих в качестве знаменателей практичные числа 6, 8, 12, 20, 24, 60 и 100.

Воуз^[8] показал, что любое число x/y имеет представление в виде египетской дроби с ${\displaystyle \scriptstyle O({\sqrt {\log y}})}$ членами. Доказательство использует поиск последовательности практичных чисел n_i со свойством, что любое число, меньшее n_i, может быть записано в виде суммы ${\displaystyle \scriptstyle O({\sqrt {\log n_{i-1}}})}$ различных делителей числа n_i. Тогда i выбирается так, что ${\displaystyle n_{i-1}<y\leqslant n_{i}}$ и ${\displaystyle xn_{i}}$ делится на y, давая частное q и остаток r. Из этого выбора следует, что ${\displaystyle \scriptstyle {\frac {x}{y}}={\frac {q}{n_{i}}}+{\frac {r}{yn_{i}}}}$. Разложив числители в правой части формулы на сумму делителей числа n_i получим представление числа в виде египетской дроби. Тененбаум и Йокота^[9] использовали подобную технику, использующую другую последовательность практичных чисел, чтобы показать, что любое число x/y имеет представление в виде египетской дроби, в которой наибольший знаменатель равен ${\displaystyle \scriptstyle O({\frac {y\log ^{2}y}{\log \log y}})}$.

Согласно сентябрьской 2015 года гипотезе Чжи-Вэй Сунь^[10] любое положительное рациональное число имеет представление в виде египетской дроби, в котором любой знаменатель является практичным числом. Существует доказательство гипотезы в блоге Дэвида Эппштейна^[11].

Одна из причин интереса к практичным числам заключается в том, что многие из их свойств подобны свойствам простых чисел. Более того, теоремы, аналогичные гипотезе Гольдбаха и гипотезе о числах-близнецах, известны для практичных чисел — любое положительное чётное число является суммой двух практичных чисел и существует бесконечно много троек практичных чисел ${\displaystyle x-2,x,x+2}$^[12]. Джузеппе Мелфи показал также, что существует бесконечно много практичных чисел Фибоначчи (последовательность A124105 в OEIS). Аналогичный вопрос о существовании бесконечного числа простых чисел Фибоначчи^[англ.] остаётся открытым. Хаусман и Шапиро^[13] показали, что существует всегда практичное число в интервале ${\displaystyle [x^{2},(x+1)^{2}]}$ для любого положительного вещественного x, что является аналогом гипотезы Лежандра для простых чисел.

Пусть p(x) подсчитывает количество практичных чисел, не превосходящих x. Маргенштерн^[7] высказал гипотезу, что p(x) асимптотически равна cx/log x для некоторой константы c, что напоминает формулу в теореме о распределении простых чисел и усиливает более раннее утверждение Эрдёша и Локстона^[14], что практичные числа имеют плотность ноль в множестве целых чисел. Сайес^[15] доказал, что для подходящих констант c₁ и c₂

${\displaystyle c_{1}{\frac {x}{\log x}}<p(x)<c_{2}{\frac {x}{\log x}},}$

Наконец, Вайнгартнер^[16] доказал гипотезу Маргенштерна, показав, что

${\displaystyle p(x)={\frac {cx}{\log x}}\left(1+O\!\left({\frac {\log \log x}{\log x}}\right)\right),}$

для ${\displaystyle x\geqslant 3}$ и некоторой константы ${\displaystyle c>0}$.

• Tables of practical numbers Архивная копия от 26 декабря 2017 на Wayback Machine compiled by Giuseppe Melfi.
• Practical Number (англ.) на сайте PlanetMath.
• Weisstein, Eric W. Practical Number (англ.) на сайте Wolfram MathWorld.