Предварение равноденствий
Предваре́ние равноде́нствий (от. лат. praecessio aequinoctiorum), также Преце́ссия земно́й оси́ — историческое название для постепенного смещения точек весеннего и осеннего равноденствий (то есть точек пересечения небесного экватора с эклиптикой) по звёздному небу навстречу видимому годичному движению Солнца. Другими словами, каждый звёздный год весеннее равноденствие наступает немного раньше, чем в предыдущем году, — примерно на 20 минут 24 секунды[1]. В угловых единицах смещение составляет сейчас около 50,3" в год, или 1 градус каждые 71,6 года[2]. Это смещение является периодическим, и примерно каждые 25 776 лет точки равноденствия возвращаются на прежние места.
Предварение равноденствий не означает, что времена года перемещаются по календарю; применяемый в наши дни григорианский календарь отражает длину не звёздного, а тропического года, который соответствует интервалу от равноденствия до равноденствия. Поэтому эффект предварения равноденствий фактически включён в действующий календарь[3].
Причины


Основная причина предварения равноденствий — прецессия, периодическое изменение направления земной оси под влиянием притяжения Луны, а также (в меньшей степени) Солнца. Как указал Ньютон в своих «Началах», сплюснутость Земли вдоль оси вращения приводит к тому, что гравитационное притяжение тел солнечной системы вызывает прецессию земной оси[4]; позже выяснилось, что к аналогичным последствиям приводит неоднородность плотности распределения масс внутри Земли. Величина прецессии пропорциональна массе возмущающего тела и обратно пропорциональна кубу расстояния до него; чем быстрее вращается прецессирующее тело, тем меньше скорость его прецессии[5].
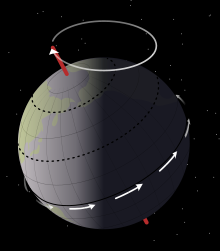
В результате прецессии земная ось описывает в пространстве конус. Поворот земной оси смещает и связанную с Землёй экваториальную систему небесных координат относительно удалённых, практически неподвижных на небесной сфере звёзд. На небесной сфере ось описывает окружность так называемого малого круга небесной сферы с центром в северном полюсе эклиптики для северного полушария и в южном полюсе эклиптики — для южного полушария, с угловым радиусом примерно 23,5 градуса[6]. Полный оборот по этой окружности происходит с периодом (по современным данным), составляющим примерно 25 800 лет. В течение года скорость земной прецессии, вызванной данным небесным телом, меняется — например, для Солнца она максимальна в дни солнцестояния, а в дни равноденствия равна нулю[7].
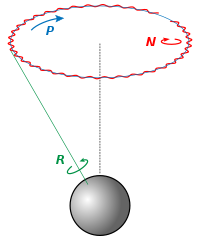
Существуют и другие причины смещения земной оси, в первую очередь — нутация, периодическое, быстрое относительно периода прецессии, «покачивание полюсов». Период нутации земной оси равен 18,61 года, и её средняя амплитуда составляет около 17" (угловых секунд). При этом нутация, в отличие от прецессии, изменяет в небольших пределах угол наклона земной оси к плоскости эклиптики[8].
Кроме Луны и Солнца, прецессионное смещение вызывают и другие планеты (в основном из-за уменьшения наклона плоскости эклиптики к экватору), но оно невелико, в сумме примерно 12 угловых секунд в столетие и направлено противоположно лунно-солнечной прецессии[6][5][7]. Имеются и другие факторы, возмущающие направление земной оси — апериодическое «блуждание полюсов[англ.]», изменения океанических течений, движение атмосферных масс, сильные землетрясения, изменяющие форму геоида и т. п., однако их вклад в смещение земной оси по сравнению с прецессией и нутацией ничтожен[9].
Аналогичные явления происходят на других планетах и их спутниках. Например, ось Юпитера под влиянием его многочисленных спутников и Солнца смещается на −3,269 секунды дуги в год[10] (в начале XX века предполагалось, что угловая скорость прецессии юпитерианской оси составляет примерно полградуса за юпитерианский год, или примерно в 50 раз больше настоящего значения[5]). Ось Марса прецессирует с угловой скоростью −7,6061(35) секунды дуги в год[11]. Существует и лунная прецессия двух типов — орбитальная прецессия с периодом 8,85 года и прецессия узлов с периодом 18,6 года.
Последствия




Поворот оси нашей планеты имеет разнообразные последствия. Направление прецессионного смещения противоположно направлению осевого вращения Земли, поэтому прецессия сокращает продолжительность тропического года, измеряемого от равноденствия до равноденствия. Другими словами, тропический год становится на 20 минут короче звёздного. Поскольку долготы звёзд отсчитываются от точки равноденствия, все они постепенно увеличиваются (на 50,26" ежегодно) — именно этот эффект исторически привёл к открытию данного явления[15].
В ходе прецессии вид звёздного неба, наблюдаемый в тех или иных широтах, меняется, так как меняются склонения тех или иных созвездий, может меняться даже сезон их наблюдения. Некоторые созвездия, видимые сейчас в средних широтах северного полушария Земли (например, Орион и Большой Пёс), постепенно опускаются под горизонт и через несколько тысяч лет будут почти недоступны для этих широт, зато на северном небе появятся созвездия Центавр, Южный Крест и ряд других. Конечно, не все созвездия южного полушария будут доступны в результате прецессии — выше всех поднимется современное «летнее» небо, меньше — «осеннее» и «весеннее», зимнее небо, наоборот, опустится, так как в настоящее время оно максимально «поднято»[5].
Схожие процессы будут и в Южном полушарии. Многие созвездия Северного полушария, которые в настоящее время не показываются в Южном, станут там видны, причём выше всего поднимется современное «зимнее» небо, которое видно из Южного полушария как летнее. Например, спустя 6 тысяч лет будет доступно из средних широт Южного полушария для наблюдения созвездие Большая Медведица, а 6 тысяч лет назад там была видна Кассиопея[5].
Полюс мира сейчас почти совпадает с Полярной звездой. Во времена строительства Великих пирамид в древнем Египте (около 4700 лет назад) он находился вблизи звезды Тубан (α Дракона). После 2103 года полюс начнёт удаляться от Полярной звезды и в V тысячелетии перейдёт в созвездие Цефея, а через 12 000 лет роль «полярной звезды» станет играть Вега. Античные астрономы видели точку весеннего равноденствия в созвездии Овна, а точку осеннего равноденствия — в созвездии Весов, поэтому обе точки до сих пор принято обозначать символами этих созвездий, хотя они переместились в созвездие Рыб и созвездие Девы соответственно[6][15].
Угол наклона земной оси относительно полюса эклиптики меняется в пределах от 22,0° до 24,5° со средним периодом 41 000 лет. Также в пределах около 4° колеблется плоскость эклиптики, в результате плоскость экватора меняет свой наклон в интервале примерно от 18° до 28° относительно эклиптики 1850 года[16].
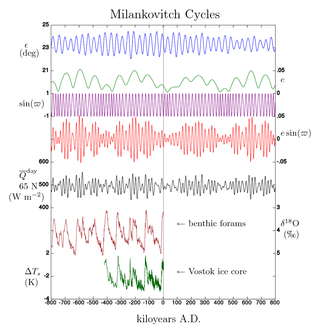
Предполагаемое влияние на климат Земли прецессии и других астрономических факторов остаётся дискуссионной темой[17]; см. об этом статью Циклы Миланковича.
Исторический очерк
На основании некоторых косвенных данных предполагают, что различие между звёздным и тропическим годом (простым логическим следствием чего является движение точек равноденствия на фоне звёзд) впервые установил в III веке до н. э. Аристарх Самосский. Разность между звёздным и тропическим годом, вычисленная на основании этих данных, соответствует скорости прецессии 1° за 100 лет, или 36" в год[18] (по современным данным, 1° за 71,6 года).

Исходя из наблюдений звёзд, предварение равноденствий было открыто выдающимся древнегреческим астрономом Гиппархом во II веке до н. э. В его распоряжении были результаты наблюдений греческого астронома III века до н. э. Тимохариса, из которых Гиппарх обнаружил, что все долготы звёзд увеличиваются примерно (по его оценке) на 1° каждые 100 лет. Во II веке н. э. существование прецессии подтвердил Клавдий Птолемей, причём скорость прецессии по его данным составляла всё те же 1° в 100 лет[19].
Большинство астрономов доптолемеева периода полагали, что все звёзды закреплены на одной сфере (сфере неподвижных звёзд), являющейся границей Вселенной. Видимое суточное вращение небосвода при этом считалось отражением вращения этой сферы вокруг своей оси — оси мира. Для объяснения прецессии Птолемей был вынужден ввести за пределами сферы неподвижных звёзд (на рисунке слева обозначена цифрой 1) ещё одну сферу, которая вращается с периодом в одни сутки вокруг оси мира (NS). К ней прикреплена сфера неподвижных звёзд 2, вращающаяся с периодом прецессии вокруг оси AD, перпендикулярной плоскости эклиптики. Таким образом, вращение сферы звёзд есть суперпозиция двух вращений, суточного и прецессионного. Наконец, внутрь этой сферы вложена ещё одна сфера 3, вращающаяся вокруг той же оси AD, но в противоположном направлении, что компенсирует прецессионное движение для всех внутренних сфер (но эта сфера по-прежнему принимает участие в суточном вращении)[20].
В V веке н.э. существование прецессии подверг сомнению знаменитый философ, математик и астроном Прокл Диадох, но её существование подтвердил его ученик Аммоний, сын Гермия.
Теон Александрийский, комментатор Птолемея (IV век), выдвинул гипотезу, что сфера неподвижных звёзд испытывает периодические колебания в пределах 8°, после чего возвращается в прежнее положение. Это явление было названо трепидацией. В IX веке эту модель поддержал знаменитый арабский астроном Сабит ибн Курра[21][22]. Уже арабские астрономы более позднего времени показали, что прецессия носит монотонный характер. Тем не менее, они полагали, что скорость прецессии периодически изменяется, так что изменение долгот звёзд можно разложить на две составляющие: равномерное увеличение (собственно прецессия), на которое наложено периодическое колебание (трепидация). Такой точки зрения придерживался, в том числе, Николай Коперник, и лишь Тихо Браге доказал полное отсутствие трепидации[5]. Ат-Туси и Браге к этому времени с хорошей точностью оценили величину прецессии: 51 угловая секунда за год[23].
Коперник первым понял, что смещается не небесный экватор, а земная ось, и получил скорость прецессии, близкую к современным представлениям — 1° за 72 года. Причина смещения была подробно объяснена в «Началах» Ньютона, причём Ньютон отдельно выделил вклад в эту величину Луны и Солнца[4]. В математической модели Ньютона Земля была мысленно разделена на шарообразную часть и кольцеобразное экваториальное утолщение; из открытых Ньютоном законов механики следовало, что притяжение Луны создаёт для утолщения дополнительный момент силы, приводящий к повороту земной оси. Этот момент силы наиболее велик тогда, когда Луна максимально удалена от плоскости земного экватора. Аналогичный механизм действует со стороны Солнца[6][5]. Рассуждения Ньютона были принципиально верны, хотя его математическая модель и содержала неточности, так как плотность Земли не является постоянной, а параметры ньютоновской модели (массы Луны и Солнца, расстояния до них) были в то время известны с большой погрешностью.
В XVIII веке большой вклад в изучение вопроса внесли двое учёных. Джеймс Брэдли открыл нутацию, составил таблицы, позволявшие учитывать при точных астрономических измерениях прецессию, нутацию и аберрацию света. Даламбер в своём труде «Исследование предварения равноденствий» (Recherches sur la precession des equinoxes, 1749) исправил и развил модель Ньютона, дал первую теорию нутации[23]. В XIX веке теорию прецессии в основном завершили Фридрих Вильгельм Бессель и Отто Вильгельм Струве[5].
Ведущий американский астроном Саймон Ньюком в 1896 году дал формулу прецессии, которая показывала и скорость изменения её величины[2]:
- Здесь T — число лет, прошедших после 1900 года.
В 1976 году XVI съезд Международного астрономического союза в Гренобле уточнил формулу Ньюкома и принял за новую базу 2000 год[2]:
- Здесь T — число лет, прошедших после 2000 года.
См. также
Примечания
- ↑ Михайлов А. А., 1978, Глава «Почему изменяется склонение звёзд?».
- ↑ 1 2 3 Михайлов А. А., 1978, Глава «Как измерить прецессию?».
- ↑ Прецессия Архивная копия от 17 августа 2016 на Wayback Machine.
- ↑ 1 2 Еремеева А. И., Цицин Ф. А., 1989, с. 183.
- ↑ 1 2 3 4 5 6 7 8 ЭСБЕ, 1890—1907.
- ↑ 1 2 3 4 Михайлов А. А., 1978, Глава «Всегда ли Полярная останется Полярной».
- ↑ 1 2 Жаров В. Е., 2002, с. 354—355.
- ↑ Кононович, Мороз, 2011, с. 114—115.
- ↑ Куликов К. А. Движение полюсов Земли. — Изд. 2-е. — М.: Изд-во АН СССР, 1962. — 87 с. — (Научно-популярная серия).
- ↑ Le Maistre S., Folkner W.M., Jacobson R.A., Serra D. Jupiter spin-pole precession rate and moment of inertia from Juno radio-science observations // Planetary and Space Science. — 2016. — Vol. 126. — P. 78—92. — doi:10.1016/j.pss.2016.03.006. — .
- ↑ Kuchynka P. et al. New constraints on Mars rotation determined from radiometric tracking of the Opportunity Mars Exploration Rover // Icarus. — 2014. — Vol. 229. — P. 340—347. — doi:10.1016/j.icarus.2013.11.015. — .
- ↑ Бакулин П. И. Курс общей астрономии. — 4-е изд.. — М.: «Наука», 1977. — 544 с.
- ↑ J. Vondrak, N. Capitaine, P. Wallace. New precession expressions, valid for long time intervals.. — 2011. Архивировано 25 января 2023 года.
- ↑ Vondrák, J.; Capitaine, N.; Wallace, P. (2011-10-01). "New precession expressions, valid for long time intervals". Astronomy & Astrophysics (англ.). 534: A22. doi:10.1051/0004-6361/201117274. ISSN 0004-6361. Архивировано 5 марта 2023. Дата обращения: 26 февраля 2023.
- ↑ 1 2 Кононович, Мороз, 2011, с. 115—116.
- ↑ A. L. Berger (1976), Obliquity and precession for the last 5000000 years., Архивировано из оригинала 4 сентября 2019, Дата обращения: 10 ноября 2020
- ↑ Циклы Миланковича. Элементы. Дата обращения: 4 августа 2016. Архивировано 30 мая 2012 года.
- ↑ Rawlins D. Continued-Fraction Decipherment: Ancestry of Ancient Yearlengths & (pre-Hipparchan) Precession (англ.) // DIO: The International Journal of Scientific History. — 1999. — Vol. 9.1. — P. 31—38. Архивировано 9 февраля 2005 года.
- ↑ Еремеева А. И., Цицин Ф. А., 1989, с. 88—91.
- ↑ Evans J. The History and Practice of Ancient Astronomy. — New York: Oxford University Press, 1998.
- ↑ Рожанская М. М., 1976.
- ↑ Куртик Г. Е., 1986.
- ↑ 1 2 Колчинский И. Г., Корсунь А. А., Родригес М. Г. Астрономы. Биографический справочник. — Киев: Наукова думка, 1986. — С. 42—43, 83, 249.
Литература
- Теория прецессии
- Белова Н. А. Вращательное движение Земли // Курс сферической астрономии (глава V). — М.: Недра, 1971. — 183 с.
- Жаров В. Е. Прецессия и нутация // Сферическая астрономия (глава 6). — М.: Век 2, 2002. — ISBN 5-85099-168-9. (Математическое описание прецессии)
- Кононович Э. В., Мороз В. И. Общий курс астрономии. — 4-е изд.. — М.: Книжный дом «ЛИБРОКОМ», 2011. — 544 с. — (Классический университетский учебник). — ISBN 978-5-397-01644-5.
- Михайлов А. А., академик. Прецессия // Земля и Вселенная. — 1978. — № 2.
- Прецессия : [арх. 15 июня 2022] / В. А. Самсонов, В. Е. Жаров // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- Цесевич В. П. Предварение равноденствий // Что и как наблюдать на небе. — М.: Наука, 1973.
- Исторические исследования
- Еремеева А. И., Цицин Ф. А. История астрономии (основные этапы развития астрономической картины мира). — М.: Изд-во МГУ, 1989. — ISBN 5-211-00347-0.
- Куртик Г. Е. Теория восхождения и нисхождения Сабита ибн Корры. К проблеме взаимоотношения теории и наблюдений // Историко-астрономические исследования, вып. XVIII. — М., 1986. — С. 111—150.
- Рожанская М. М. Механика на средневековом Востоке. — Москва: Наука, 1976.
- Evans J. The History and Practice of Ancient Astronomy (англ.). — New York: Oxford University Press, 1998.
Ссылки
- Серафимов В. Прецессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Sert, Josée. Hipparchus’s understanding of the precession (англ.). Дата обращения: 25 июля 2016.
- Ulansey D. Hipparchus and the precession of the equinoxes (англ.). Дата обращения: 25 июля 2016.