Предел Шокли — Квиссера
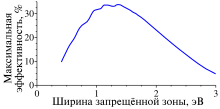
Предел Шокли — Квиссера (предел детального баланса, предел эффективности Шокли — Квиссера) — максимальная теоретическая эффективностью солнечного элемента, использующего одиночный p-n переход для сбора энергии, где единственный механизм потерь — излучательная рекомбинация в солнечном элементе. Впервые предел был рассчитан Уильямом Шокли и Хансом-Йоахимом Квиссером из компании Shockley Semiconductor в 1961 году, что дало максимальную эффективность 30 % при энергии фотонов 1,1 эВ[1]. Это ограничение является одним из самых фундаментальных в производстве солнечной энергии с помощью фотоэлектрических элементов и считается одним из самых важных вкладов в эту область[2].
Этот первый расчёт использовал спектр чёрного тела с температурой 6000 K как приближение к солнечному спектру. Последующие расчеты использовали измеренные глобальные солнечные спектры, AM 1,5, и включали зеркало на задней поверхности, которое увеличивает максимальную эффективность преобразования солнечной энергии до 33,16 % для солнечного элемента с одним p-n-переходом с оптимальной шириной запрещённой зоны 1,34 эВ[3]. То есть из всей мощности, содержащейся в солнечном свете (около 1000 Вт/м²), падающей на идеальный солнечный элемент, только 33,7 % могут быть когда-либо превращены в электричество (или 337 Вт/м²). Самый популярный материал для солнечных элементов, кремний, имеет менее благоприятную ширину запрещённой зоны 1,1 эВ, в результате чего максимальная эффективность составляет около 32 %. Современные коммерческие монокристаллические солнечные элементы обеспечивают эффективность преобразования около 24 %, потери в основном связаны с практическими проблемами, такими как отражение от передней части элемента и блокирование света тонкими проводами на поверхности элемента.
Предел Шокли — Квиссера применим только к обычным солнечным элементам с одним p-n-переходом; солнечные батареи с несколькими слоями и солнечные тепловые и некоторые другие солнечные энергетические системы могут превзойти этот предел. В лучшем случае для многопереходного солнечного элемента с бесконечным числом слоёв соответствующий предел составляет 68,7 % для обычном солнечного света[4] или 86,8 % при использовании концентрированного солнечного света[5].
Основы

В традиционном твёрдотельном полупроводнике, таком как кремний, солнечный элемент состоит из двух легированных кристаллов, один из которых представляет собой полупроводник n-типа, в котором есть дополнительные свободные электроны, а другой — полупроводник p-типа, в котором отсутствуют свободные электроны, но есть дырки. При первоначальном контакте друг с другом некоторые электроны в части n-типа проводимости перетекают в часть с p-типом проводимости, чтобы «заполнить» недостающие электроны. В конце концов через границу переместится достаточно частиц, чтобы уравнять уровни Ферми двух материалов. Результатом является область на границе раздела — p-n-переход, где носители заряда обеднены с каждой стороны интерфейса. В кремнии такой перенос электронов создаёт потенциальный барьер примерно 0,6—0,7 В[6].
Когда материал помещается на солнце, фотоны солнечного света могут поглощаться полупроводником с p-типом проводимости, в результате чего электроны в валентной зоне продвигаются по энергии в зону проводимости. Этот процесс известен как фотовозбуждение. Электроны в зоне проводимости могут свободно перемещаться по полупроводнику. Когда нагружается цепь с ячейкой в целом, эти электроны будут перетекать со стороны р-типа на сторону n-типа, терять энергию при движении по внешней цепи, а затем возвращаться в материал р-типа, где они могут воссоединиться с оставленными ими дырками в валентной зоне. Таким образом, солнечный свет создаёт электрический ток[6].
Предел
Предел Шокли — Квиссера рассчитывается путём изучения количества электрической энергии, извлекаемой на каждый фотон падающего солнечного света. Есть несколько следующих соображений.
Излучение абсолютно чёрного тела
Любой материал, находящийся не при абсолютном нуле температур, излучает электромагнитное излучение за счёт эффекта излучения абсолютно чёрного тела. Для ячейки при комнатной температуре это составляет примерно 7 % всей энергии, падающей на солнечный элемент.
Любая потеря энергии в солнечном элементе превращается в тепло, поэтому любая неэффективность в ячейке приводит к увеличению температуры элемента, помещённом под солнечный свет. По мере повышения температуры ячейки уходящее излучение и потери тепла за счёт теплопроводности и конвекции также увеличиваются, пока не будет достигнуто равновесие. На практике это равновесие обычно достигается при температурах до 360 K, и, следовательно, элементы обычно работают с более низкой эффективностью, чем при комнатной температуре. В спецификациях модуля эта зависимость от температуры обычно указана как TNOCT (NOCT — номинальная рабочая температура солнечного элемента).
Для «абсолютно чёрного тела» при нормальных температурах очень малая часть этого излучения (количество в единицу времени и на единицу площади определяется как Qc, «c» для «ячейки» англ. cell) — это фотоны с энергией, превышающей ширину запрещённой зоны (длина волны менее примерно 1,1 микрон для кремния), и часть этих фотонов (Шокли и Квайссер используют коэффициент tc) генерируются рекомбинацией электронов и дырок, что уменьшает величину тока, который мог бы генерироваться в противном случае. Это очень небольшой эффект, но Шокли и Квайссер предположили, что общая скорость рекомбинации, когда напряжение на элементе равно нулю (короткое замыкание или отсутствие света), пропорциональна излучению абсолютно чёрного тела Qc. Эта скорость рекомбинации даёт отрицательный вклад в эффективность солнечного элемента. Шокли и Квайссер рассчитали, что Qc составляет 1700 фотонов в секунду на квадратный сантиметр для кремния при температуре 300 К.
Рекомбинация

Поглощение фотона создаёт электронно-дырочную пару, которая потенциально может способствовать возникновению тока. Однако в соответствии с принципом детального равновесия возможен и обратный процесс: электрон и дырка могут встретиться и рекомбинировать, испустив фотон. Этот процесс снижает эффективность ячейки. Могут существовать и другие процессы рекомбинации, но рассмотрение этого вклада необходимо.
В модели Шокли — Квиссера скорость рекомбинации зависит от напряжения на солнечном элементе, но остаётся неизменной независимо от того, падает ли на него свет. Коэффициент даёт отношение скорости рекомбинации, вызывающей излучение, к скорости общей рекомбинации, поэтому скорость рекомбинации на единицу площади, когда «=» 0 равно и, таким образом, зависит от потока фотонов абсолютно чёрного тела с энергией выше энергии запрещённой зоны. Множитель 2 был включён в предположении, что излучение, испускаемое ячейкой, идёт в обоих направлениях. (Это на самом деле спорно, если отражающая поверхность используется на затенённой стороне.) При ненулевом напряжении концентрации носителей заряда (электронов и дырок) изменяются (уравнение Шокли для диода), и, по данным авторов, скорость рекомбинации изменяется в , где — напряжение, эквивалентное температуре солнечного элемента, или «тепловое напряжение», а именно:
- где — заряд электрона.
Таким образом, скорость рекомбинации в этой модели пропорциональна умноженному на излучение абсолютно чёрного тела с энергией выше ширины запрещённой зоны:
(На самом деле это приближение, верное, пока солнечный элемент достаточно толстый, чтобы действовать как абсолютно чёрное тело, к более точному выражению[7][8]
Однако разница в максимальной теоретической эффективности пренебрежимо мала, за исключением крошечной ширины запрещённой зоны ниже 200 мэВ[9].)
Скорость генерации электронно-дырочных пар не из-за падающего солнечного света остаётся неизменной, поэтому рекомбинация минус спонтанная генерация равна
- где
(Шокли и Квиссер принимают fc за константу, хотя и допускают, что она сама может зависеть от напряжения.)
Скорость генерации электронно-дырочных пар под действием солнечного света равна
- где — число фотонов, превышающих энергию запрещённой зоны, попадающих на солнечный элемент на единицу площади,
- — их доля, создающая электронно-дырочную пару.
Эта скорость генерации называется потому что это ток «короткого замыкания» (на единицу площади). Когда есть нагрузка, то не будет равно нулю и возникает ток равный скорости генерации пар за счёт солнечного света за вычетом разницы между рекомбинацией и спонтанной генерацией:
Таким образом, напряжение холостого хода определяется (при условии, что не зависит от напряжения) как:
Произведение тока короткого замыкания и напряжения холостого хода Шокли и Квиссер называют «номинальной мощностью». На самом деле невозможно получить такое количество энергии из солнечного элемента, но мы можем приблизиться.
Отношение напряжения холостого хода к напряжению запрещённой зоны Шокли и Квиссер называют Для разомкнутой цепи:
Асимптотически это даёт:
или:
где Vs — напряжение, эквивалентное температуре солнца. Когда отношение Vc/Vs стремится к нулю, то напряжение холостого хода становится равным напряжению запрещённой зоны, а когда оно приближается к единице, то напряжение холостого хода становится равным нулю. Вот почему КПД падает, если солнечный элемент нагревается. Фактически это выражение представляет собой термодинамический верхний предел количества работы, которую можно получить от источника тепла при температуре солнца и отвода тепла при температуре ячейки.
Спектральные потери
Поскольку акт перемещения электрона из валентной зоны в зону проводимости требует затраты энергии, только фотоны с большим количеством энергии будут создавать электронно-дырочную пару. В кремнии зона проводимости находится на расстоянии около 1,1 эВ от валентной зоны, что соответствует инфракрасному свету с длиной волны около 1,1 эВ. Другими словами, фотоны красного, жёлтого и синего света, а также некоторые ближние инфракрасное излучение будут способствовать выработке энергии, в то время как радиоволны, микроволны и большинство инфракрасных фотонов — нет[10]. Это накладывает немедленный предел на количество энергии, которую можно извлечь из солнца. Из полной мощности потока 1000 Вт/м² солнечного света (модель AM1.5) около 19 % имеют энергию менее 1,1 эВ и не производят энергию в кремниевом солнечном элементе.
Ещё одним важным фактором потерь является то, что теряется любая энергия, превышающая ширину запрещенной зоны. Хотя энергия синего света примерно в два раза больше энергии красного света, эта энергия не улавливается устройствами с одним p-n-переходом. Электрон выбрасывается в зону проводимости с более высокой энергией при столкновении с синим фотоном, но он теряет эту дополнительную энергию, когда движется к p-n-переходу (энергия преобразуется в тепло)[10]. Это составляет около 33 % падающего солнечного света, что означает для кремния только из-за потерь в спектре теоретический предел эффективности преобразования составляет около 48 %, без учёта всех других факторов.
Существует компромисс в выборе ширины запрещённой зоны. Если ширина запрещённой зоны велика, то не так много фотонов создают пары, тогда как, если ширина запрещённой зоны мала, электронно-дырочные пары не содержат столько энергии.
Шокли и Квиссер называют коэффициент эффективности, связанный с потерями спектра u, «функцией предельной эффективности». Они подсчитали, что наилучшая ширина запрещённой зоны для солнечного света составляет 1,1 эВ, значение для кремния, и даёт значение u, равное 44 %. Они использовали излучение абсолютно чёрного тела с температурой 6000 К для солнечного света и обнаружили, что оптимальная ширина запрещённой зоны будет иметь энергию 2,2 kTs.(При этом значении 22 % энергии излучения абсолютно чёрного тела будет лежать ниже ширины запрещённой зоны.) Использование более точного спектра может дать немного другой оптимум. абсолюьно чёрное тело на 6000 К выдает 7348 Вт на квадратный сантиметр, поэтому значение u равно 44 % и значение 5,73⋅1018 фотонов на джоуль (соответствует ширине запрещённой зоны 1,09 V, значение, использованное Шокли и Квиссером), даёт Qs равную 1,85⋅1022 фотонов в секунду на квадратный сантиметр.
Согласование импедансов
Если сопротивление нагрузки слишком велико, ток будет очень низким, а если сопротивление нагрузки слишком мало, то падение напряжения на ней будет очень низким. Существует оптимальное сопротивление нагрузки, которое будет потреблять наибольшую мощность от солнечного элемента при заданном уровне освещённости. Шокли и Квиссер называют отношение извлекаемой мощности к IshVoc коэффициентом согласования импеданса m. (Его также называют коэффициентом заполнения.) Оптимум зависит от формы кривой зависимости I от V. Для очень слабого освещения кривая представляет собой более или менее диагональную линию, а m будет равно 1/4. Но для большой освещенности m приближается к 1. Шокли и Квиссер приводят график, показывающий m как функцию отношения zoc напряжения холостого хода к тепловому напряжению Vc. По мнению авторов, это отношение хорошо аппроксимируется выражением ln(fQs/Qc), где f — комбинация факторов fsfωts/(2tc), в которой fω — телесный угол солнца разделённый на π. Согласно авторам, максимальное значение f без концентрации света (например, с отражателями) равно fω/2, или 1,09⋅10−5. Используя вышеупомянутые значения Qs и Qc, даёт отношение напряжения холостого хода к тепловому напряжению 32,4 (Voc равно 77 % ширины запрещённой зоны). Авторы получили уравнение
которое можно решить, чтобы найти zm, отношение оптимального напряжения к тепловому напряжению. Для zoc, равного 32,4, мы находим zm равным 29,0. Тогда можно использовать формулу
чтобы найти коэффициент согласования импеданса. Для zoc 32,4 это составляет 86,5 %.
Все факторы
Учитывая только потери спектра, солнечный элемент имеет максимальную теоретическую эффективность 48 % (или 44 %, согласно Шокли и Квиссеру — их «предельный коэффициент эффективности»). Таким образом, потери в спектре составляют большую часть потерянной мощности. С учётом эффектов рекомбинации и зависимости I от V эффективность описывается следующим уравнением:
где
где u, v и m — соответственно предельный коэффициент полезного действия, отношение напряжения холостого хода Vop к напряжению запрещёной зоны Vg и коэффициент согласования импеданса (всё обсуждалось выше), а Vc — тепловое напряжение, и Vs — напряжение, эквивалентное температуре Солнца. Принимая ts равным 1 и используя упомянутые выше значения 44 %, 77 % и 86,5 % для трёх факторов, мы получаем общую эффективность около 29 %. Шокли и Квиссер в абстракте статьи говорят о 30 %, но не приводят подробных расчётов. Более поздняя ссылка даёт для однопереходного элемента теоретическую пиковую производительность около 33,7 %, или около 337 Вт/м² в AM1.5[1][10].
Когда количество солнечного света увеличивается с помощью отражателей или линз, коэффициент fω (и, следовательно, f) будет больше. Это повышает как v, так и m. Шокли и Квиссер включают график, показывающий общую эффективность как функцию ширины запрещённой зоны для различных значений f . При значении 1 график показывает максимальную эффективность чуть более 40 %, приближаясь к предельной эффективности (по их расчетам) в 44 %.
Другие соображения
Работа Шокли и Квиссера рассматривала только самую основную физику; но существует ряд других факторов, которые ещё больше снижают теоретическую эффективность.
Ограниченная подвижность
Когда электрон выбрасывается в результате фотовозбуждения, атом, с которым он ранее был связан, остается с чистым положительным зарядом. В нормальных условиях атом отрывает электрон от соседнего атома, чтобы нейтрализовать себя. Затем этот атом попытается отобрать электрон у другого атома и так далее, вызывая цепную реакцию ионизации, которая проходит через ячейку. Поскольку их можно рассматривать как движение положительного заряда, полезно называть их «дырками», своего рода виртуальным положительным электроном.
Как и электроны, дырки движутся в материале и будут притягиваться к источнику электронов. Обычно они обеспечиваются электродом на задней поверхности солнечного жлемента. Тем временем электроны зоны проводимости движутся вперёд к электродам на передней поверхности. По разным причинам дырки в кремнии движутся гораздо медленнее, чем электроны. Это означает, что за конечное время, пока электрон движется вперёд к p-n-переходу, он может встретить медленно движущуюся дырку, оставленную предыдущим фотовозбуждением. Когда это происходит, электрон рекомбинирует на этом атоме, и энергия теряется (обычно из-за испускания фотона с этой энергией, но есть множество возможных процессов).
Рекомбинация устанавливает верхний предел скорости генерации; после определённой скорости генерации в материале движется так много дырок, что новые электроны никогда не доберутся до p-n-перехода. В кремнии это снижает теоретические характеристики при нормальных условиях работы ещё на 10 % сверх указанных выше тепловых потерь. Материалы с более высокой подвижностью электронов (или дырок) могут улучшить характеристики кремния; солнечные элементы на основе арсенида галлия (GaAs) выигрывают около 5 % в реальных примерах только благодаря этому эффекту. При более ярком свете, когда он концентрируется, например, зеркалами или линзами, этот эффект усиливается. Обычные кремниевые элементы быстро насыщаются, в то время как GaAs продолжает улучшаться при концентрациях до 1500 раз.
Безызлучательная рекомбинация
Рекомбинация между электронами и дырками вредна для солнечного элемента, поэтому разработчики стараются свести её к минимуму. Однако излучательная рекомбинация, когда электрон и дырка рекомбинируют, создавая фотон, выходящий из ячейки в воздух, неизбежна, потому что это обращённый во времени процесс поглощения света. Поэтому расчёт Шокли — Квиссера учитывает излучательную рекомбинацию; но предполагается (оптимистично), что другого источника рекомбинации нет. Более реалистичные пределы, которые ниже предела Шокли — Квиссера, могут быть рассчитаны с учётом других причин рекомбинации. К ним относятся рекомбинация на дефектах и границах зерен.
В кристаллическом кремнии, даже если кристаллические дефекты отсутствуют, всё равно имеет место оже-рекомбинация, которая происходит гораздо чаще, чем излучательная рекомбинация. С учётом этого эффекта теоретический КПД кристаллических кремниевых солнечных элементов был рассчитан на уровне 29,4 %[11].
Поглощение зависит от частоты
Частотная зависимость поглощения и, по сути, коэффициент отражения материалов можно учесть при расчёте эффективности солнечного элемента[12][13]. Согласно пределу Шокли — Квиссера, эффективность полупроводниковых солнечных элементов зависит от ширины запрещённой зоны полупроводника. Здесь предполагается, что оптическое поглощение начинается выше ширины запрещённой зоны материала. Однако из-за конечной температуры возможны оптические возбуждения ниже оптической щели. Это хорошо видно по хвосту мнимой диэлектрической проницаемости ниже оптической щели в зависимости от температуры[14]. Поскольку мнимая диэлектрическая проницаемость, хотя и низкая, отлична от нуля ниже оптической щели, то даже при энергии фотонов ниже оптической щели происходит поглощение света. Для достаточно толстых материалов это может привести к значительному поглощению. В пределе Шокли — Квиссера предполагается 100%-ное поглощение света выше ширины запрещённой зоны полупроводника, чтобы найти максимально возможную эффективность солнечного элемента в случае, если коэффициент отражения снизится до нуля, например, за счёт использования просветляющего покрытия. Однако проблема с этим предположением заключается в том, что поглощением ниже ширины запрещённой зоны материала при конечных температурах пренебрегают, что может повлиять на эффективность. При учёте поглощения ниже ширины запрещённой зоны нижний предел интеграла тока короткого замыкания изменяется с ширины запрещённой зоны на нуль, и поэтому уравнение определяется как;
где Jsc — ток короткого замыкания, A — зависящая от толщины поглощательная способность материала, Jph — поток солнечной энергии AM1,5, а ω — частота света.
Превышение предела

Анализ Шокли и Квиссера основывался на следующих предположениях:
- на каждый входящий фотон возбуждается одна электронно-дырочная пара;
- происходит термическая релаксация энергии электронно-дырочной пары выше запрещённой зоны;
- освещение происхлдит неконцентрированным солнечным светом.
Ни одно из этих предположений не обязательно верно, и для значительного превышения базового предела использовался несколько различных подходов.
Ячейки с множественными переходами
Наиболее широко исследованным путём к солнечным элементам с более высокой эффективностью были фотоэлектрические элементы с множественными переходами, также известные как тандемные элементы. Эти солнечные элементы используют несколько p-n-переходов, каждый из которых настроен на определённую частоту спектра. Это уменьшает проблему, обсуждавшуюся выше, заключающуюся в том, что материал с одной заданной шириной запрещённой зоны не может поглощать солнечный свет ниже ширины запрещённой зоны и не может в полной мере использовать солнечный спектр намного выше ширины запрещённой зоны. В наиболее распространённой конструкции солнечный элемент с большой шириной запрещённой зоны находится сверху, поглощая высокоэнергетический свет с более короткой длиной волны и пропуская остальную часть. Под ним находится солнечный элемент с более низкой шириной запрещённой зоны, который поглощает часть низкоэнергетического длинноволнового света. Под этой может быть ещё одна ячейка, всего с четырьмя слоями.
Расчёт фундаментальных пределов эффективности этих многопереходных ячеек работает так же, как и для солнечных элементов с одним переходом, с той оговоркой, что часть света будет преобразована в другие частоты и переизлучена внутри структуры. Использование методов, аналогичных исходному анализу Шокли — Квиссера, с учётом этих соображений даёт аналогичные результаты; двухслойная ячейка может достигать эффективности 42 %, трёхслойная ячейка — 49 %, а теоретический солнечный элемент с бесконечным количеством слоёв — 86 % при несконцентрированном солнечном свете[5].
В большинстве тандемных ячеек, которые были созданы на сегодняшний день, используются три слоя, настроенные на синий (вверху), жёлтый (посередине) и красный (внизу). Эти солненые элементы требуют использования полупроводников, которые можно настроить на определённые частоты, что привело к тому, что большинство из них сделано из соединений арсенида галлия (GaAs), часто германия для красного, GaAs для жёлтого и GaInP2 для синего. Их производство очень дорого с использованием технологий, аналогичных конструированию микропроцессоров, но с размерами «чипов» в несколько сантиметров. В тех случаях, когда единственным соображением является прямая производительность, эти ячейки стали обычным явлением; они широко используются, например, в спутниковых приложениях, где отношение мощности к весу перевешивает практически все остальные соображения. Их также можно использовать в концентрированных фотогальванических приложениях, где относительно небольшой солнечный элемент может обслуживать большую площадь.
Тандемные ячейки не ограничиваются высокопроизводительными приложениями; они также используются для изготовления фотоэлектрических элементов средней эффективности из дешёвых, но низкоэффективных материалов. Одним из примеров являются солнечные элементы из аморфного кремния, где тандемные элементы с тройным соединением коммерчески доступны от Uni-Solar и других компаний.
Концентрация света
Солнечный свет можно сконцентрировать линзами или зеркалами до гораздо большей интенсивности. Интенсивность солнечного света является параметром в расчёте Шокли — Квиссера, и с большей концентрацией теоретический предел эффективности несколько увеличивается. Если, однако, интенсивный свет нагревает солнечный элемент, что часто происходит на практике, теоретический предел эффективности может снизиться с учётом всех обстоятельств.
На практике выбор использования концентрации света основывается в первую очередь на других факторах, помимо небольшого изменения эффективности солнечных элементов. Эти соображения включают относительную стоимость площади солнечных элементов по сравнению с фокусирующей оптикой, такой как линзы или зеркала, стоимость систем слежения за солнцем, долю света, успешно сфокусированного на солнечном элементе, и так далее.
Для концентрации солнечного света можно использовать широкий выбор оптических систем, включая обычные линзы и изогнутые зеркала, линзы Френеля, массивы небольших плоских зеркал и люминесцентные солнечные концентраторы[15][16]. В альтернативном подходе предлагается разместить массив микроскопических солнечных элементов на поверхности и сфокусировать на них свет с помощью массивов микролинз[17], в то время как ещё одно предложение предлагает разработать массив полупроводниковых нанопроволок таким образом, чтобы свет концентрировался в нанопроволоках[18].
Фотогальваника промежуточного диапазона
Была проведена некоторая работа по созданию состояний средней энергии в монокристаллических структурах. Эти элементы будут сочетать в себе некоторые преимущества элементов с множественными переходами с простотой существующих кремниевых конструкций. Детальный расчёт предела для этих ячеек с бесконечными запрещёнными зонами предполагает максимальную эффективность 77,2 %[19]. На сегодняшний день ни одна коммерческая ячейка с использованием этой технологии не производилась.
Преобразование фотонов с повышением частоты
Как обсуждалось выше, фотоны с энергией ниже ширины запрещённой зоны теряются в обычных однопереходных солнечных элементах. Один из способов уменьшить эти потери — использовать преобразование фотонов с повышением частоты, то есть включение в модуль молекулы или материала, которые могут поглощать два или более фотона с энергией ниже запрещённой зоны, а затем излучать один фотон с энергией выше запрещённой зоны. Другая возможность — использовать двухфотонное поглощение, но это может работать только при очень высокой концентрации света[20].
Преобразование теплового фотона с повышением частоты
Тепловое преобразование с повышением частоты основано на поглощении фотонов с низкими энергиями в повышающем преобразователе, который нагревается и повторно излучает фотоны с более высокими энергиями[21]. Эффективность повышающей конверсии может быть увеличена за счёт управления оптической плотностью состояний поглотителя[22], а также за счёт настройки характеристик излучения по выделенному углу. Например, плоская платформа для теплового преобразования с повышением частоты может иметь переднюю поверхность, поглощающую низкоэнергетические фотоны, падающие в узком диапазоне углов, и заднюю поверхность, эффективно излучающую только высокоэнергетические фотоны[23]. Теоретически было предсказано, что гибридная термофотоэлектрическая платформа, использующая тепловое преобразование с повышением частоты, продемонстрирует максимальную эффективность преобразования 73 % при освещении несконцентрированным солнечным светом. Детальный анализ неидеальных гибридных платформ, допускающих до 15 % потерь на поглощение/переизлучение, дал предельное значение эффективности 45 % для Si PV-ячеек.
Захват горячих электронов
Один из основных механизмов потерь связан с потерей избыточной энергии носителей с энергией выше запрещённой зоны. Неудивительно, что было проведено значительное количество исследований способов улавливания энергии носителей до того, как они потеряют её в кристаллической решётке[24]. Одной из исследуемых систем для этого являются квантовые точки[25].
Множественная генерация экситонов
Родственная концепция заключается в использовании полупроводников, которые генерируют более одного возбуждённого электрона на поглощённый фотон вместо одного электрона на краю зоны. Квантовые точки были тщательно исследованы на предмет этого эффекта, и было показано, что они работают на длинах волн, соответствующих солнечному свету, в прототипах солнечных элементов[25][26].
Другой, более простой способ использования генерации множественных экситонов — это процесс, называемый синглетным делением (или делением синглетного экситона), при котором синглетный экситон преобразуется в два триплетных экситона с более низкой энергией. Это позволяет достичь более высокой теоретической эффективности при соединении с полупроводником с малой шириной запрещённой зоны[27], а также сообщалось о квантовой эффективности, превышающей 100 %[28].
Также в материалах, в которых (возбуждённые) электроны сильно взаимодействуют с остальными электронами, таких как изоляторы Мотта, может генерироваться несколько экситонов[29].
Флуоресцентное преобразование с понижением частоты/передачи с понижением
Другой возможностью повышения эффективности является преобразование частоты света в сторону ширины запрещённой зоны с помощью флуоресцентного материала. В частности, для превышения предела Шокли — Квиссера необходимо, чтобы флуоресцентный материал преобразовывал один высокоэнергетический фотон в несколько фотонов с более низкой энергией (квантовая эффективность > 1). Например, один фотон с более чем удвоенной энергией запрещённой зоны может дать на два фотона с энергией выше ширины запрещённой зоны. На практике, однако, этот процесс преобразования имеет тенденцию быть относительно неэффективным. Если бы была найдена очень эффективная система, то такой материал можно было бы нанести на переднюю поверхность стандартной ячейки, повысив её эффективность при небольших затратах[30]. Напротив, значительный прогресс был достигнут в исследовании флуоресцентной передачи с понижением, который преобразует высокоэнергетический свет (например, ультрафиолетовый свет) в низкоэнергетический свет (например, красный свет) с квантовой эффективностью меньше 1. Ячейка может быть более чувствительна к этим низкоэнергетическим фотонам. Красители, редкоземельные люминофоры и квантовые точки активно исследуются на предмет флуоресцентной передачи с понижением[31]. Например, кремниевые квантовые точки позволили снизить передачу, что привело к повышению эффективности современных кремниевых солнечных элементов[32].
Термофотоэлектрическое преобразование с понижением частоты
Термофотоэлектрические элементы похожи на фосфоресцентные системы, но используют пластину в качестве понижающего преобразователя. Солнечная энергия, падающая на пластину, обычно окрашенную в чёрный цвет, повторно излучается в виде низкоэнергетического инфракрасного излучения, которое затем можно улавливать в инфракрасной ячейке. Это зависит от наличия практической ИК-ячейки, но можно рассчитать теоретическую эффективность преобразования. Для преобразователя с шириной запрещённой зоны 0,92 эВ эффективность ограничена 54 % для солнечного жлемента с одним переходом и 85 % для концентрированного света, падающего на идеальные компоненты без оптических потерь и с учётом только излучательной рекомбинации[33].
Примечания
- ↑ 1 2 3 William Shockley (March 1961). "Detailed Balance Limit of Efficiency of p-n Junction Solar Cells" (PDF). Journal of Applied Physics. 32 (3): 510—519. Bibcode:1961JAP....32..510S. doi:10.1063/1.1736034. Архивировано (PDF) 11 мая 2019. Дата обращения: 5 августа 2023.
- ↑ Hans Queisser. Computer History Museum. Дата обращения: 17 января 2017. Архивировано 13 декабря 2018 года.
- ↑ S. Rühle (2016). "Tabulated values of the Shockley—Queisser limit for single junction solar cells". Solar Energy. 130: 139—147. Bibcode:2016SoEn..130..139R. doi:10.1016/j.solener.2016.02.015.
- ↑ A. De Vos (1981). "On the Thermodynamic Limit of Photovoltaic Energy Conversion". Appl. Phys. 25 (2): 119—125. Bibcode:1981ApPhy..25..119D. doi:10.1007/BF00901283.
- ↑ 1 2 De Vos, A. (1980). "Detailed balance limit of the efficiency of tandem solar cells". Journal of Physics D: Applied Physics. 13 (5): 839—846. Bibcode:1980JPhD...13..839D. doi:10.1088/0022-3727/13/5/018.
- ↑ 1 2 Photovoltaic Cells (Solar Cells), How They Work. specmat.com. Дата обращения: 2 мая 2007. Архивировано из оригинала 18 мая 2007 года.
- ↑ A. De Vos (1981). "On the Thermodynamic Limit of Photovoltaic Energy Conversion". Appl. Phys. 25 (2): 119—125. Bibcode:1981ApPhy..25..119D. doi:10.1007/BF00901283.
- ↑ W. Ruppel (1980). "Upper limit for the conversion of solar energy". IEEE Transactions on Electron Devices. 27 (4). Bibcode:1980ITED...27..877R. doi:10.1109/T-ED.1980.19950. This paper finds the same open-circuit voltage and short-circuit current as de Vos and Pauwels, but does not give the correct function for I(V).
- ↑ Byrnes. The Shockley-Queisser limit. Дата обращения: 10 марта 2016. Архивировано 10 марта 2016 года.
- ↑ 1 2 3 C. S. Solanki and G. Beaucarne, «Advanced Solar Cell Concepts» (недоступная ссылка), Interuniversity Microelectronics Center, Belgium
- ↑ A. Richter (Oct 2013). "Reassessment of the limiting efficiency for crystalline silicon solar cells". IEEE Journal of Photovoltaics. 3 (4): 1184—1191. doi:10.1109/JPHOTOV.2013.2270351.
- ↑ B. Ozdemir, V. Barone (2020). "Thickness dependence of solar cell efficiency in transition metal dichalcogenides MX2 (M: Mo, W; X: S, Se, Te)". Solar Energy Materials and Solar Cells. 212: 110557. doi:10.1016/j.solmat.2020.110557.
- ↑ S. Kim, J. A. Márquez, T. Unold, A. Walsh (2020). "Upper limit to the photovoltaic efficiency of imperfect crystals from first principles". Energy & Environmental Science. 13: 1481—1491. doi:10.1039/D0EE00291G.
{{cite journal}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка) - ↑ P. Lautenschlager, M. Garriga, L. Vina, M. Cardona (1987). "Temperature dependence of the dielectric function and interband critical points in silicon". Phys. Rev. B. 36 (9): 4821—4830. Bibcode:1987PhRvB..36.4821L. doi:10.1103/PhysRevB.36.4821. PMID 9943498.
{{cite journal}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка) - ↑ Elizabeth A. Thomson, «MIT opens new 'window' on solar energy» Архивная копия от 28 марта 2014 на Wayback Machine, MIT News, 10 July 2008
- ↑ Kittidachachan, Pattareeya (19 December 2007). "Photon Collection Efficiency of Fluorescent Solar Collectors" (PDF). CHIMIA International Journal for Chemistry. 61 (12): 780—786. doi:10.2533/chimia.2007.780. Архивировано (PDF) 5 августа 2023. Дата обращения: 5 августа 2023.
- ↑ Microsystems Enabled Photovoltaics, Sandia National Laboratories. Дата обращения: 26 марта 2013. Архивировано из оригинала 5 апреля 2013 года.
- ↑ Krogstrup, Peter (24 March 2013). "Single-nanowire solar cells beyond the Shockley—Queisser limit". Nature Photonics. 7 (4): 306—310. arXiv:1301.1068. Bibcode:2013NaPho...7..306K. doi:10.1038/nphoton.2013.32.
- ↑ Brown, Andrew S. (2002). "Impurity photovoltaic effect: Fundamental energy conversion efficiency limits". Journal of Applied Physics. 92 (3). Bibcode:2002JAP....92.1329B. doi:10.1063/1.1492016.
- ↑ Jalali, Bahram (2009). "Green Silicon Photonics". Optics and Photonics News. 20 (6). doi:10.1364/OPN.20.6.000018.
- ↑ Ekins-Daukes, N. J. (2003). "Photovoltaic efficiency enhancement through thermal up-conversion". Applied Physics Letters. 82 (12). Bibcode:2003ApPhL..82.1974E. doi:10.1063/1.1561159.
- ↑ Farrell, D. J. (2011). "A hot-carrier solar cell with optical energy selective contacts". Applied Physics Letters. 99 (11). Bibcode:2011ApPhL..99k1102F. doi:10.1063/1.3636401.
- ↑ Boriskina, Svetlana V. (2014). "Exceeding the solar cell Shockley—Queisser limit via thermal up-conversion of low-energy photons". Optics Communications. 314: 71—78. arXiv:1310.5570. Bibcode:2014OptCo.314...71B. doi:10.1016/j.optcom.2013.10.042.
- ↑ Gavin Conibeer et al., «Hot Carrier Solar Cell: Implementation of the Ultimate Photovoltaic Converter» Архивная копия от 25 января 2022 на Wayback Machine, Global Climate & Energy Project, Stanford University, September 2008
- ↑ 1 2 A. J. Nozik, «Quantum Dot Solar Cells» Архивная копия от 16 марта 2023 на Wayback Machine, National Renewable Energy Laboratory, October 2001
- ↑ Semonin, O. E. (2011). "Peak External Photocurrent Quantum Efficiency Exceeding 100% via MEG in a Quantum Dot Solar Cell". Science. 334 (6062): 1530—1533. Bibcode:2011Sci...334.1530S. doi:10.1126/science.1209845. PMID 22174246. Архивировано 5 августа 2023. Дата обращения: 5 августа 2023.
- ↑ Ehrler, B. (2012). "Singlet Exciton Fission-Sensitized Infrared Quantum Dot Solar Cells". Nano Letters. 12 (2): 1053—1057. Bibcode:2012NanoL..12.1053E. doi:10.1021/nl204297u. PMID 22257168.
- ↑ Congreve, D. N. (2013). "External Quantum Efficiency Above 100% in a Singlet-Exciton-Fission—Based Organic Photovoltaic Cell". Science. 340 (6130): 334—337. Bibcode:2013Sci...340..334C. doi:10.1126/science.1232994. PMID 23599489. Архивировано 5 августа 2023. Дата обращения: 5 августа 2023.
- ↑ P. Werner (2014). "Role of impact ionization in the thermalization of photoexcited Mott insulators". Phys. Rev. B. 90 (23): 235102. arXiv:1408.3425. Bibcode:2014PhRvB..90w5102W. doi:10.1103/PhysRevB.90.235102.
- ↑ «Sunovia, EPIR Demonstrate Optical Down-Conversion For Solar Cells». Дата обращения: 5 августа 2023. Архивировано 13 февраля 2012 года.
- ↑ Klampaftis, Efthymios (August 2009). "Enhancing the performance of solar cells via luminescent down-shifting of the incident spectrum: A review". Solar Energy Materials and Solar Cells. 93 (8): 1182—1194. doi:10.1016/j.solmat.2009.02.020.
- ↑ Pi, Xiaodong (11 October 2012). "Enhancing the Efficiency of Multicrystalline Silicon Solar Cells by the Inkjet Printing of Silicon-Quantum-Dot Ink". The Journal of Physical Chemistry C. 116 (40): 21240—21243. doi:10.1021/jp307078g.
- ↑ Harder, Nils-Peter (2003). "Theoretical limits of thermophotovoltaic solar energy conversion". Semiconductor Science and Technology. 18 (5): S151—S157. Bibcode:2003SeScT..18S.151H. doi:10.1088/0268-1242/18/5/303.











![{\displaystyle I_{0}[\exp(V/V_{c})-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a05237b4173e67f08f867e6b8197f96e158512e)





![{\displaystyle I=I_{sh}-I_{0}[\exp(V/V_{c})-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4109f4ddc1f8a0c7f32d40cb83c95eb1f08808a)




![{\displaystyle \ln I_{sh}=\ln I_{0}+\ln[\exp(V/V_{c})-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7fc424af18f05ebd1ed7e989dfbcd4281c51c2f)





















