Предел вдоль фильтра (предел по базису фильтра, предел по базе) — обобщение понятия предела.
Определение фильтра
Пусть дано множество  Непустая система
Непустая система  подмножеств множества
подмножеств множества  называется базисом фильтра (базой) множества
называется базисом фильтра (базой) множества  , если
, если
- для любого
 выполнено
выполнено 
- для любых
 существует
существует  такое, что
такое, что 
Определение предела
Везде далее  — базис фильтра (база) множества
— базис фильтра (база) множества  .
.
Предел числовой функции
Пусть  . Число
. Число  называется пределом функции
называется пределом функции  по базе
по базе  если
если
- для любого
 существует
существует  такое, что для всех
такое, что для всех  выполнено неравенство
выполнено неравенство 
Обозначение предела по базе: 
Предел функции со значениями в метрическом пространстве
Пусть  — метрическое пространство и
— метрическое пространство и  . Точка
. Точка  называется пределом функции
называется пределом функции  по базе
по базе  если
если
- для любого
 существует
существует  такое, что для всех
такое, что для всех  выполнено неравенство
выполнено неравенство 
Обозначение: 
Предел функции со значениями в топологическом пространстве
Пусть  — топологическое пространство и
— топологическое пространство и  . Точка
. Точка  называется пределом функции
называется пределом функции  по базе
по базе  если
если
- для любой окрестности
 точки
точки  существует
существует  такое, что
такое, что  , то есть для всех
, то есть для всех  выполняется включение
выполняется включение  .
.
Обозначение: 
Замечание. Последнее «равенство» корректно использовать лишь в случаях, когда пространство  — хаусдорфово. Пределом функции со значениями в нехаусдорфовом пространстве могут быть сразу несколько различных точек (и, таким образом, нарушается теорема о единственности предела).
— хаусдорфово. Пределом функции со значениями в нехаусдорфовом пространстве могут быть сразу несколько различных точек (и, таким образом, нарушается теорема о единственности предела).
Примеры
Обычный предел
Пусть  — топологическое пространство, и
— топологическое пространство, и  Пусть
Пусть  Тогда система множеств
Тогда система множеств

является базисом фильтра множества  и обозначается
и обозначается  или просто
или просто  Предел функции по базе
Предел функции по базе  множества
множества  называется пределом функции в точке
называется пределом функции в точке  и обозначается записью
и обозначается записью  .
.
Односторонние пределы
Основная статья: Односторонние пределы
- Пусть
 и
и  Тогда система множеств
Тогда система множеств

является базисом фильтра и обозначается  или
или  Предел
Предел  называется правосторонним пределом функции
называется правосторонним пределом функции  при
при  стремящемся к
стремящемся к 
- Пусть
 и
и  Тогда система множеств
Тогда система множеств

является базисом фильтра и обозначается  или
или  Предел
Предел  называется левосторонним пределом функции
называется левосторонним пределом функции  при
при  стремящемся к
стремящемся к 
Пределы на бесконечности
Основная статья: Пределы функции на бесконечности
- Пусть
 и
и  Тогда система множеств
Тогда система множеств

является базисом фильтра и обозначается  или
или  Предел
Предел  называется пределом функции
называется пределом функции  при
при  стремящемся к бесконечности.
стремящемся к бесконечности.
- Пусть
 и
и  Тогда система множеств
Тогда система множеств

является базисом фильтра и обозначается  Предел
Предел  называется пределом функции
называется пределом функции  при
при  стремящемся к минус-бесконечности.
стремящемся к минус-бесконечности.
Предел последовательности
Система множеств  где
где

является базисом фильтра и обозначается  Функция
Функция  называется числовой последовательностью, а предел
называется числовой последовательностью, а предел  пределом этой последовательности.
пределом этой последовательности.
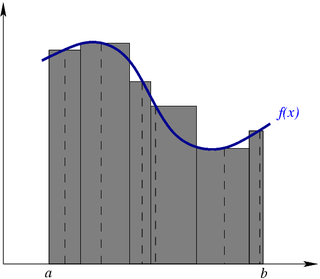
Интеграл Римана
Пусть ![{\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bada51108a3f44e79ed5224741286fc4a5a904ad) Назовём размеченным разбиением отрезка
Назовём размеченным разбиением отрезка ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) пару
пару  такую, что
такую, что ![{\displaystyle \forall i\in \{1,\cdots ,n\}\ \ x_{i-1}<x_{i}\land \xi _{i}\in [x_{i-1},x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4c469cb2e7f582b44417e96e9c88ab1308d31b) Назовём диаметром разбиения
Назовём диаметром разбиения  число
число  Тогда система множеств
Тогда система множеств  где
где

является базисом фильтра в пространстве  всех размеченных разбиений
всех размеченных разбиений ![{\displaystyle [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba5cb29655f824ce80a0b6a32d9326d0e8742cd) Определим функцию
Определим функцию  равенством
равенством

Тогда предел  называется интегралом Римана функции
называется интегралом Римана функции  на отрезке
на отрезке ![{\displaystyle [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba5cb29655f824ce80a0b6a32d9326d0e8742cd)
Литература
- Кудрявцев Л. Д. Курс математического анализа (в двух томах), — М.: Высшая школа, т. II — 584 с. — 1981.































































![{\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bada51108a3f44e79ed5224741286fc4a5a904ad)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle \forall i\in \{1,\cdots ,n\}\ \ x_{i-1}<x_{i}\land \xi _{i}\in [x_{i-1},x_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4c469cb2e7f582b44417e96e9c88ab1308d31b)





![{\displaystyle [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba5cb29655f824ce80a0b6a32d9326d0e8742cd)