Ги́льбертово простра́нство — обобщение евклидова пространства, допускающее бесконечную размерность и полное по метрике, порождённой скалярным произведением. Названо в честь Давида Гильберта.
Прямое произведение — множество, элементами которого являются все возможные упорядоченные пары элементов заданных двух непустых исходных множеств. Предполагается, что впервые «декартово» произведение двух множеств ввёл Георг Кантор.

Внешняя алгебра, или алгебра Грассмана, — ассоциативная алгебра, используемая в геометрии при построении теории интегрирования в многомерных пространствах. Впервые введена Грассманом в 1844 году.
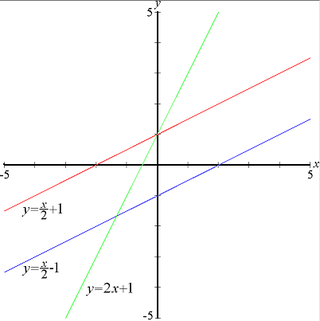
Линейная функция — функция вида
 .
.
Пото́чный или Пото́ковый шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры.
Критерий Поста — одна из центральных теорем в теории булевых функций, устанавливающая необходимое и достаточное условие для того, чтобы некоторый набор булевых функций обладал достаточной выразительностью, чтобы представить любую булеву функцию. Впервые сформулирован американским математиком Эмилем Постом.
Полином Жегалкина — многочлен над полем  , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
Пространство Соболева — функциональное пространство, состоящее из функций из пространства Лебега  , имеющих обобщённые производные заданного порядка
, имеющих обобщённые производные заданного порядка  оттуда же.
оттуда же.
Шаблон:Карточка хеш функции
Линейная булева функция — булева функция, полином Жегалкина которой имеет первую степень. Более развёрнуто булева функция  называется линейной, если она выражается в виде:
называется линейной, если она выражается в виде:


Группа Лоренца является группой Ли симметрий пространства-времени в специальной теории относительности. Эта группа может быть реализована как набор матриц, линейных преобразований или унитарных операторов на некотором гильбертовом пространстве. Группа имеет различные представления. В любой релятивистски инвариантной физической теории эти представления как-то должны быть отражены. Сама физика должна быть сделана на их основе. Более того, специальная теория относительности вместе с квантовой механикой являются двумя физическими теориями, которые тщательно проверены и объединение этих двух теорий сводится к изучению бесконечномерных унитарных представлений группы Лоренца. Это имеет как историческую важность в основном течении в теоретической физике, так и связи с более спекулятивными теориями настоящего времени.
Тест ассоциативности — проверка бинарной операции на ассоциативность. Наивная процедура проверки, заключающаяся в переборе всех возможных троек аргументов операции, требует  времени, где
времени, где  — размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за
— размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за  , если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с
, если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с  до
до  , был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время
, был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время  , что является улучшением по сравнению с поиском Гровера, работающим за
, что является улучшением по сравнению с поиском Гровера, работающим за  .
.
Ascon — семейство блочных шифров, используемых для аутентифицированного шифрования с присоединёнными данными и хеширования. Набор шифров был разработан Кристофом Добраунигом, Марией Айхелзидер, Флорианом Менделем и Мартином Шлаффером. Шифры Ascon-128 и Ascon-128a стали победителями соревнования CAESAR в категории применения в приложениях с ограниченными ресурсами.
Алгори́тм Шёнинга — вероятностный алгоритм для решения задачи выполнимости булевых формул в k-конъюнктивной нормальной форме, предложенный Уве Шёнингом в 1999 году.



















































