Математи́ческий ана́лиз — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное и интегральное исчисления.

Фу́нкция — соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого.
Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем для формализации и анализа понятия вычислимости.

Градие́нт — вектор, своим направлением указывающий направление наискорейшего роста некоторой скалярной величины  .
.
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917-го года.
Опера́тор — математическое отображение между множествами, в котором каждое из них наделено какой-либо дополнительной структурой. Понятие оператора используется в различных разделах математики для отличия от другого рода отображений ; точное значение зависит от контекста, например в функциональном анализе под операторами понимают отображения, ставящие в соответствие функции другую функцию.
Алгоритм Дойча — Йожи — квантовый алгоритм, предложенный Дэвидом Дойчем и Ричардом Йожей в 1992 году, и ставший одним из первых квантовых алгоритмов. Алгоритм основывается на явлении квантовой запутанности и принципе суперпозиции, благодаря чему демонстрирует квантовое превосходство — значительно более эффективную работу в сравнении с известными классическими алгоритмами.
Интегральное преобразование Абеля — преобразование, часто используемое при анализе сферически или цилиндрически симметричных функций. Названо в честь норвежского математика Н. Х. Абеля. Для функции  преобразование Абеля даётся уравнением
преобразование Абеля даётся уравнением

Дифференциа́льное уравне́ние в ча́стных произво́дных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию  комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией  вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Интегра́л — одно из важнейших понятий математического анализа, которое возникает при решении задач:
- о нахождении площади под кривой;
- пройденного пути при неравномерном движении;
- массы неоднородного тела, и тому подобных;
- а также в задаче о восстановлении функции по её производной.

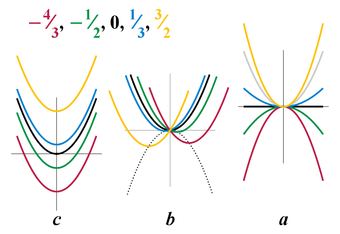
Гра́фик фу́нкции — геометрическое понятие в математике, дающее представление о геометрическом образе функции.
Скалярное поле на некотором конечномерном пространстве  — функция, ставящая в соответствие каждой точке из некоторой области этого пространства скаляр, то есть действительное или комплексное число. При фиксированном базисе пространства скалярное поле можно представить как функцию нескольких переменных, являющихся координатами точки.
— функция, ставящая в соответствие каждой точке из некоторой области этого пространства скаляр, то есть действительное или комплексное число. При фиксированном базисе пространства скалярное поле можно представить как функцию нескольких переменных, являющихся координатами точки.
E2 — в криптографии семейство симметричных блочных криптоалгоритмов на основе ячейки Фейстеля. E2 использует блок размером 128 бит и ключи длиной 128, 192, 256 бит. Создан в компании NTT в 1998 году и был представлен на AES конкурсе. Наследником данного шифра является шифр Camellia, который также является результатом творчества компании NTT.
Преобразование Меллина — преобразование, которое можно рассматривать как мультипликативную версию двустороннего преобразования Лапласа. Это интегральное преобразование тесно связано с теорией рядов Дирихле и часто используется в теории чисел и в теории асимптотических разложений. Преобразование Меллина тесно связано с преобразованием Лапласа и преобразованием Фурье, а также теорией гамма-функций и теорией смежных специальных функций.
Преобразование Фурье на группах — обобщение дискретного преобразования Фурье от циклических к локально компактным абелевым группам или произвольным компактным группам.