Произведение Адамара
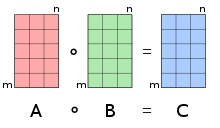
Произведение Адамара[1] (произведение Шура[2], покомпонентное произведение) — бинарная операция над двумя матрицами одинаковой размерности, результатом которой является матрица той же размерности, в которой каждый элемент с индексами — это произведение элементов с индексами исходных матриц. Операция названа в честь французского математика Жака Адамара и немецкого математика Исая Шура.
Определение и свойства
Для двух матриц одинаковой размерности произведение Адамара определено как покомпонентное произведение двух матриц:
Для двух матриц, которые имеют разные размерности, произведение Адамара не определено.
Пример для матриц 3×3:
- .
Является ассоциативной и дистрибутивной операцией и, в отличие от обычного произведения матриц, коммутативно:
- ,
- ,
- .
Свойства смешанных произведений с другими вариантами умножения матриц:
- , где — произведение Кронекера;
- , где — торцевое произведение[3];
- , где — столбцовое произведение Хатри — Рао.
Приложения
Используется в алгоритмах сжатия с потерями, например, JPEG.
В программных пакетах MATLAB и GNU Octave операция используется как стандартная операция умножения массивов и обозначается символом «.*»[4].
Операция произведения над векторными типами данных в GPGPU-технологиях программирования также реализована по принципу произведения Адамара. Другие примитивные математические операции над векторными типами данных реализованы как покомпонентные операции над их компонентами.
Блочная версия

Проникающее торцевое произведение
Данный тип матричной операции базируется на произведении Адамара и позволяет поэлементно умножать матрицу на произвольное количество блоков той же размерности , образующих блочную матрицу [5]:
- .
Например, для
получим:
- .
Основные свойства:
- ;
- ,
где - символ торцевого произведения матриц.
- , где - вектор.
Данный вид матричного умножения был предложен в 1998 г. Слюсарем В.И. для описания откликов цифровой антенной решётки с неидентичными приёмными каналами[5]. Кроме того, это произведение позволяет формализовать процесс функционирования свёрточной нейросети. Например, если рассматривать указанную матрицу как массив пикселей изображения на входе нейросетевого алгоритма, то блоки матрицы будут соответствовать различным наборам коэффициентов, используемым для формирования свёрточного слоя в нескольких параллельных каналах обработки изображения нейросетью[6].
Операция проникающего торцевого произведения вектора и матрицы реализована в библиотеке машинного обучения TensorFlow с помощью встроенной функции "tf.multiply"[6][7].
Примечания
- ↑ Million, Elizabeth The Hadamard Product. Дата обращения: 2 января 2012. Архивировано 12 июня 2013 года.
- ↑ Davis, Chandler. «The norm of the Schur product operation.» Numerische Mathematik 4.1 (1962): 343—344.
- ↑ Slyusar, V. I. End products in matrices in radar applications // Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3. — 1996. — 27 декабря. — С. 50—53. Архивировано 27 июля 2020 года.
- ↑ Arithmetic Operators + - * / \ ^ ' -. MATLAB documentation. MathWorks. Дата обращения: 2 января 2012. Архивировано из оригинала 24 апреля 2012 года.
- ↑ 1 2 Slyusar, V. I. A Family of Face Products of Matrices and its properties (англ.) // Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz. 1999. : journal. — 1998. — 13 March (vol. 35, no. 3). — P. 379—384. — doi:10.1007/BF02733426. Архивировано 25 января 2020 года.
- ↑ 1 2 Слюсар В.И. Тензорно-матричная модель нейросетей. // Всеукраїнська науково-практична Iнтернет-конференція “Автоматизація та комп’ютерно-інтегровані технології у виробництві та освіті: стан, досягнення, перспективи розвитку”, 15 - 21 березня 2021 року, м. Черкаси, Черкаський національний університет імені Богдана Хмельницького [1]
- ↑ Tensorflow, how to multiply a 2D tensor (matrix) by corresponding elements in a 1D vector. – 2017. Дата обращения: 17 января 2021. Архивировано 15 октября 2021 года.
Литература
- Хорн Р. Матричный анализ: Пер. с англ. / Р. Хорн, Ч. Джонсон. – М.: Мир, 1989.– 655 с.

















![{\displaystyle \mathbf {A} [\circ ]\mathbf {B} =\left[{\begin{array}{c | c | c | c }\mathbf {A} \odot \mathbf {B} _{1}&\mathbf {A} \odot \mathbf {B} _{2}&\ ...\ &\mathbf {A} \odot \mathbf {B} _{n}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a459df8d26ad11a261decaaa074c51778c5fd8f6)
![{\displaystyle \mathbf {A} =\left[{\begin{array}{c}1&2&3\\4&5&6\\7&8&9\end{array}}\right],\quad \mathbf {B} =\left[{\begin{array}{c | c | c }\mathbf {B} _{1}&\mathbf {B} _{2}&\mathbf {B} _{3}\end{array}}\right]=\left[{\begin{array}{c c c | c c c | c c c }1&4&7&2&8&14&3&12&21\\8&20&5&10&25&40&12&30&6\\2&8&3&2&4&2&7&3&9\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9641997828b98145e460a5d51ae04061860dce38)
![{\displaystyle \mathbf {A} [\circ ]\mathbf {B} =\left[{\begin{array}{c c c | c c c | c c c }1&8&21&2&16&42&3&24&63\\32&100&30&40&125&240&48&150&36\\14&64&27&14&32&18&49&24&81\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c43da3f56eee534b69ab24976d7826a87a3e371)
![{\displaystyle \mathbf {A} [\circ ]\mathbf {B} =\mathbf {B} [\circ ]\mathbf {A} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/39da27a289706aa8da37ea3611b797adfc31e157)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/861e013501c6602cb57058543bfe9ca9f409492d)
![{\displaystyle \mathbf {c} \bullet \mathbf {M} =\mathbf {c} [\circ ]\mathbf {M} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b9def408e42cb688035b3d6fe7a905be7f60999)

























