
Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.

Сфе́ра Ри́мана — наглядное изображение множества  в виде сферы, подобно тому, как множество действительных чисел изображают в виде прямой и как множество комплексных чисел изображает в виде плоскости. По этой причине термин «сфера Римана» часто используется как синоним к термину «множество комплексных чисел, дополненных бесконечно удалённой точкой», наряду с термином «расширенная комплексная плоскость».
в виде сферы, подобно тому, как множество действительных чисел изображают в виде прямой и как множество комплексных чисел изображает в виде плоскости. По этой причине термин «сфера Римана» часто используется как синоним к термину «множество комплексных чисел, дополненных бесконечно удалённой точкой», наряду с термином «расширенная комплексная плоскость».
В термодинамике и физике твёрдого тела модель Дебая — метод, развитый Дебаем в 1912 г. для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая, согласно закону Дебая, пропорциональна  . В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.
. В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.
Ме́тод максима́льного правдоподо́бия или метод наибольшего правдоподобия в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия. Основан на предположении о том, что вся информация о статистической выборке содержится в функции правдоподобия. Метод максимального правдоподобия был проанализирован, рекомендован и значительно популяризирован Р. Фишером между 1912 и 1922 годами.
А́том водоро́да — физико-химическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра, как правило, входит протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон образует электронную оболочку; наибольшая вероятность обнаружения электрона в единичном объёме наблюдается для центра атома. Интегрирование по сферическому слою показывает, что наибольшая вероятность обнаружения электрона в единичном слое соответствует среднему радиусу, равному боровскому радиусу  ангстрема.
ангстрема.
Эллипти́ческий интегра́л — некоторая функция  над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
 ,
,
Гауссов пучок — пучок электромагнитного излучения, в котором распределение электрического поля и излучения в поперечном сечении хорошо аппроксимируется функцией Гаусса. Когерентный световой пучок с гауссовым распределением поля имеет фундаментальное значение в теории волновых пучков. Этот пучок называют основной модой в отличие от других мод более высокого порядка.
Ядро Пуассо́на — ядро, используемое для решения двумерного уравнения Лапласа с учетом граничных условий Дирихле в единичном круге. Ядро можно представить как производную функции Грина для уравнения Лапласа. Ядро названо в честь С. Пуассона.
Пространства Бесова  — полные квазиметрические пространства функций, являющиеся банаховыми при 1 ≤ p, q ≤ ∞. Названы в честь разработчика — советского математика Олега Владимировича Бесова. Эти пространства, наравне с определяемыми похожим образом пространствами Трибеля — Лизоркина, являются обобщением более простых функциональных пространств и применяются для определения свойств регулярности функций.
— полные квазиметрические пространства функций, являющиеся банаховыми при 1 ≤ p, q ≤ ∞. Названы в честь разработчика — советского математика Олега Владимировича Бесова. Эти пространства, наравне с определяемыми похожим образом пространствами Трибеля — Лизоркина, являются обобщением более простых функциональных пространств и применяются для определения свойств регулярности функций.

Тета-функции — это специальные функции от нескольких комплексных переменных. Они играют важную роль во многих областях, включая теории абелевых многообразий, пространства модулей и квадратичных форм. Они применяются также в теории солитонов. После обобщения к алгебре Грассмана функции появляются также в квантовой теории поля.

Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом. Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.
Векторными сферическими гармониками являются векторные функции, преобразующиеся при вращениях системы координат так же, как скалярные сферические функции с теми же индексами, или определенные линейные комбинации таких функций.
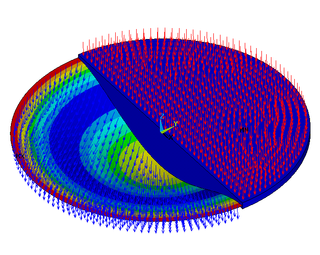
Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах, под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально имеет плоскую форму.

В математике существует несколько интегралов, известных как интеграл Дирихле, названные в честь немецкого математика Петера Густава Лежена Дирихле, один из которых является несобственным интегралом функции sinc по положительной действительной прямой:

Мультипольное излучение — излучение, обусловленное изменением во времени мультипольных моментов системы. Используется для описания электромагнитного или гравитационного излучения от изменяющегося во времени (нестационарного) распределения удалённых источников. Мультипольное разложение применяется к физическим явлениям, которые происходят на разных масштабах — от гравитационных волн из-за столкновения галактик до гамма-излучения в результате радиоактивного распада. Мультипольное излучение анализируется способами, схожими с применяемыми для мультипольного разложения полей от стационарных источников. Однако есть важные отличия, поскольку поля мультипольного излучения ведут себя несколько иначе полей от стационарных источников. Эта статья в первую очередь касается электромагнитного мультипольного излучения, хотя гравитационные волны рассматриваются аналогично.
Почти периодическая функция — это функция на множестве вещественных чисел, которая периодична с любой желаемой точностью, если заданы достаточно большие равномерно распределённые «почти периоды». Концепцию первым изучал Харальд Бор и её впоследствии обобщили, среди прочих, Вячеслав Васильевич Степанов, Герман Вейль и Абрам Самойлович Безикович. Есть также понятие почти периодических функций на локально компактных абелевых группах, которое первым изучал Джон фон Нейман.
Анализ парциальных волн в контексте квантовой механики относится к методу решения задач рассеяния путём разложения каждой волны на составляющие её компоненты углового момента и построения решения с использованием граничных условий.





























