
Геоме́трия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. В практических задачах геометрия позволяет предсказывать геометрические размеры тела, зная другие геометрические размеры этого тела с помощью известных геометрических законов.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

Проекти́вная пло́скость — двумерное проективное пространство. Важным частным случаем является вещественная проективная плоскость.
Проективное преобразование проективной плоскости — это преобразование, переводящее прямые в прямые.
Проективная геометрия — раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции.
Однородные координаты ― система координат, используемая в проективной геометрии, подобно тому, как декартовы координаты используются в евклидовой геометрии.
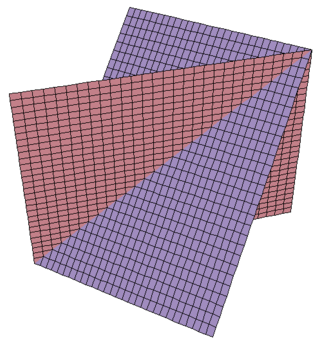
Пло́скость — одно из фундаментальных понятий в геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. В тесной связи с плоскостью принято рассматривать принадлежащие ей точки и прямые; они также, как правило, вводятся как неопределяемые понятия, свойства которых задаются аксиоматически.

Алгебраическая геометрия — раздел математики, который объединяет алгебру и геометрию. Главным предметом изучения классической алгебраической геометрии, а также в широком смысле и современной алгебраической геометрии, являются множества решений систем алгебраических уравнений. Современная алгебраическая геометрия во многом основана на методах общей алгебры для решения задач, возникающих в геометрии.
Важное свойство проективной плоскости — «симметрия» ролей, которые играют точки и прямые в определениях и теоремах, и двойственность является формализацией этой концепции. Имеются два подхода к концепции двойственности: один, использующий язык «принципа двойственности», позволяет объявить ряд теорем двойственными друг к другу, при этом двойственная к верной теореме тоже верна; и другой, функциональный подход, основанный на специальном отображении двойственности. Связь между подходами состоит в том, что двойственная теорема получается применением отображения двойственности к каждому объекту исходной. Возможен и координатный подход.

Двойственная кривая к заданной кривой на проективной плоскости — это кривая на двойственной проективной плоскости, состоящая из касательных к заданной гладкой кривой. В этом случае кривые называются взаимно двойственными (дуальными). Понятие может быть обобщено для негладких кривых и на многомерное пространство.

Алгебраическое многообразие — центральный объект изучения алгебраической геометрии. Классическое определение алгебраического многообразия — множество решений системы алгебраических уравнений над действительными или комплексными числами. Современные определения обобщают его различными способами, но стараются сохранить геометрическую интуицию, соответствующую этому определению.
Поверхность Веронезе — алгебраическая поверхность в пятимерном проективном пространстве, которая реализуется как образ вложения Веронезе. Существует также обобщение вложения Веронезе на произвольные размерности проективных пространств. Названа в честь итальянского математика Джузеппе Веронезе.
Геометрия инцидентности — раздел классической геометрии, изучающий структуры инцидентности, например принадлежность точки прямой.
В математике сизигетический пучок или пучок Гессе — это пучок плоских кубических эллиптических кривых на комплексной проективной плоскости, удовлетворяющих уравнению

Комплексная проективная плоскость — двумерное комплексное проективное пространство; является двумерным комплексным многообразием, его вещественная размерность равна 4.
Отношение инцидентности — это бинарное отношение между двумя различными типами объектов. Это включает понятия, которые можно выразить такими фразами как «точка лежит на прямой» или «прямая принадлежит плоскости». Наиболее существенное отношение инцидентности — между точкой P и прямой l, которое записывается как P I l. Если P I l, пара (P, l) называется флагом. В разговорном языке существует много выражений, описывающих отношение инцидентности (например, прямая проходит через точку, точка лежит на плоскости, и т. д.), однако термин «инцидентна» предпочтительнее, поскольку не предполагает дополнительных cопутствующих понятий и может быть использован симметрично, отражая свойство симметричности отношения. Утверждения, такие как «прямая l1 пересекает прямую l2», также являются утверждениями об отношении инцидентности, но в этом случае проще сказать: «существует точка P, инцидентная обоим прямым l1 и l2». Когда один тип объектов можно рассматривать как множество объектов другого типа (а именно, плоскость является множеством точек), отношение инцидентности можно рассматривать как включение.
Когерентные пучки — класс пучков, тесно связанных с геометрическими свойствами пространства-носителя. В определении когерентного пучка используется пучок колец, который хранит эту геометрическую информацию.
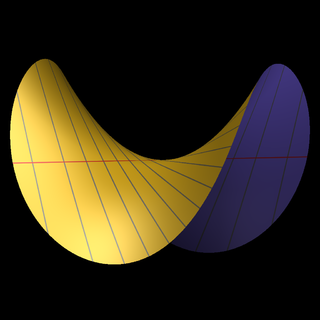
Разду́тие — операция в алгебраической геометрии. В простейшем случае оно, грубо говоря, состоит в замене точки на множество всех прямых, проходящих через неё.






















