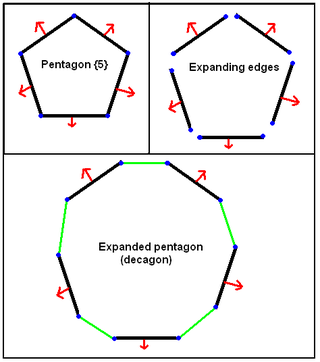
Пятиугольный многогранник
Пятиугольный многогранник — правильный многогранник в пространстве размерности n, построенный из группы Коксетера Hn. Семейству дал имя Гарольд Коксетер, поскольку двумерным пятиугольным многогранником является пятиугольник. В зависимости от его символа Шлефли он может быть назван додекаэдральным ({5, 3n − 2}) или икосаэдральным ({3n − 2, 5}).
Члены семейства
Семейство начинается с одномерных многогранников (отрезок, n = 1) и завершается бесконечным замощением 4-мерной гиперболической сферы с n = 5.
Существует два типа пятиугольных многогранников. Один тип можно назвать додекаэдральные многогранники, а другой — икосаэдральные, в зависимости от его трёхмерных частей. Эти два типа двойственны друг другу.
Додекаэдральные многогранники
Полное семейство додекаэдральных многогранников состоит из:
- Отрезок, { }
- Пятиугольник, {5}
- Додекаэдр, {5, 3} (12 пятиугольных граней)
- Стодвадцатигранник, {5, 3, 3} (120 додекаэдральных ячеек)
- Стодвадцатиячейные соты порядка 3, {5, 3, 3, 3} — замощают гиперболическое 4-мерное пространство
Фасеты любого додекаэдрального многогранника являются додекаэдральными пятиугольными многогранниками на единицу меньшей размерности. Их вершинными фигурами являются симплексы на единицу меньшей размерности.
| n | Группа Коксетера | Многоугольник Петри (проекция) | Название диаграмма Коксетера Символ Шлефли | Фасеты | Элементы | ||||
|---|---|---|---|---|---|---|---|---|---|
| Вершины | Рёбра | Грани | Ячейки[англ.] | 4-грани | |||||
| 1 | [ ] (порядок 2) | Отрезок { } | 2 вершины | 2 | |||||
| 2 | [5] (порядок 10) |  | Пятиугольник {5} | 5 рёбер | 5 | 5 | |||
| 3 | [5,3] (порядок 120) |  | Додекаэдр {5, 3} | 12 пятиугольников | 20 | 30 | 12 | ||
| 4 | [5,3,3] (порядок 14400) |  | Стодвадцатиячейник {5, 3, 3} | 120 додекаэдров | 600 | 1200 | 720 | 120 | |
| 5 | [5,3,3,3] (порядок ∞) | Стодвадцатиячейные соты {5, 3, 3, 3} | ∞ Стодвадцатиячейников | ∞ | ∞ | ∞ | ∞ | ∞ | |
Икосаэдральные многогранники
Полное семейство икосаэдральных пятиугольных многогранников состоит из:
- Отрезок, { }
- Пятиугольник, {5}
- Икосаэдр, {3, 5} (20 треугольных граней)
- Шестисотячейник, {3, 3, 5} (120 тетраэдральных ячеек)
- Пятиячейные соты пятого порядка[англ.], {3, 3, 3, 5} — замощают гиперболическое 4-мерное пространство (∞ пятиячейных фасет)
Фасеты любого икосаэдрального пятиугольного многогранника являются симплексами на единицу меньшей размерности. Вершинными фигурами многогранников являются икосаэдральные пятиугольные многогранники на единицу меньшей размерности.
| n | Группа Коксетера | Многоугольник Петри (проекция) | Название диаграмма Коксетера Символ Шлефли | Фасеты | Элементы | ||||
|---|---|---|---|---|---|---|---|---|---|
| Вершины | Рёбра | Грани | Ячейки[англ.] | 4-грани | |||||
| 1 | [ ] (порядок 2) | Отрезок { } | 2 вершины | 2 | |||||
| 2 | [5] (порядок 10) |  | Пятиугольник {5} | 5 рёбер | 5 | 5 | |||
| 3 | [5,3] (порядок 120) | 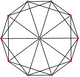 | Икосаэдр {3, 5} | 20 правильных треугольников | 12 | 30 | 20 | ||
| 4 | [5,3,3] (порядок 14400) |  | Шестисотячейник {3, 3, 5} | 600 тетраэдров | 120 | 720 | 1200 | 600 | |
| 5 | [5,3,3,3] (порядок ∞) | Пятиячейные соты пятого порядка[англ.] {3, 3, 3, 5} | ∞ Пятиячейников | ∞ | ∞ | ∞ | ∞ | ∞ | |
Связанные звёздчатые многогранники и соты
От пятиугольных многогранников могут быть образованы звёзчатые формы с получением новых звёздчатых правильных многогранников:
- В трёхмерном пространстве получаются четыре многогранника Кеплера — Пуансо — {3,5/2}, {5/2,3}, {5,5/2} и {5/2,5}.
- В четырёхмерном пространстве получаются десять многогранников Шлефли-Гесса: {3,5,5/2}[англ.],{{5/2,5,3}[англ.], {5,5/2,5}[англ.], {5,3,5/2}[англ.], {5/2,3,5}[англ.], {5/2,5,5/2}[англ.], {5,5/2,3}[англ.], {3,5/2,5}[англ.], {3,3,5/2}[англ.] и {5/2,3,3}.
- В четырёхмерном гиперболическом пространстве существуют четыре правильных звёздчатых сот: {5/2,5,3,3}[англ.], {3,3,5,5/2}[англ.], {3,5,5/2,5}[англ.] и {5,5/2,5,3}[англ.].
Примечания
Литература
- H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H. S. M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25-36]
- H.S.M. Coxeter. Regular Polytopes[англ.]. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — С. 292—293. — ISBN 0-486-61480-8.
| Основные выпуклые правильные и однородные политопы в размерностях 2—10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Семейство | An | Bn | I₂(p) / Dn | E₆ / E₇ / E₈ / F₄ / G₂ | H₄ | |||||||
| Правильный многоугольник | Правильный треугольник | Квадрат | Правильный p-угольник | Правильный шестиугольник | Правильный пятиугольник | |||||||
| Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | ||||||||
| Однородный многоячейник | Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник | |||||||
| Однородный 5-политоп | Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | |||||||||
| Однородный 6-политоп | Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | 6-полугиперкуб | 122 • 221 | ||||||||
| Однородный 7-политоп | Правильный 7-симплекс | 7-ортоплекс • 7-гиперкуб | 7-полугиперкуб | 132 • 231 • 321 | ||||||||
| Однородный 8-политоп | Правильный 8-симплекс | 8-ортоплекс • 8-гиперкуб | 8-полугиперкуб | 142 • 241 • 421 | ||||||||
| Однородный 9-политоп | Правильный 9-симплекс | 9-ортоплекс • 9-гиперкуб | 9-полугиперкуб | |||||||||
| Однородный 10-политоп | Правильный 10-симплекс | 10-ортоплекс • 10-гиперкуб | 10-полугиперкуб | |||||||||
| Однородный n-политоп | Правильный n-симплекс | n-ортоплекс • n-гиперкуб | n-полугиперкуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | |||||||
| Темы: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений | ||||||||||||