Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее значение случайной величины. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения. Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.
Обобщённая фу́нкция, или распределе́ние, — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах.
Ле́мма Фату́ — техническое утверждение, используемое при доказательстве различных теорем в функциональном анализе и теории вероятностей. Оно даёт одно из условий, при которых предел почти всюду сходящейся функциональной последовательности будет суммируемым.

Экспоненциа́льное распределе́ние — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости. В теорию характеристических функций внесли большой вклад Ю. В. Линник, И. В. Островский, К. Р. Рао, Б. Рамачандран.
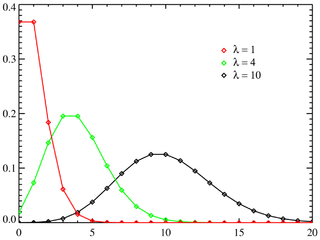
Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Производя́щая фу́нкция моме́нтов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.

Распределе́ние Ве́йбулла в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений.

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.
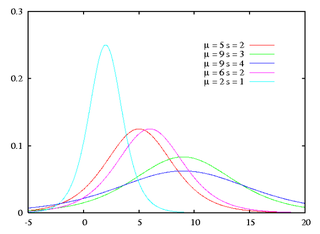
Логисти́ческое распределе́ние в теории вероятностей и математической статистике — один из видов абсолютно непрерывных распределений. Формой напоминает нормальное распределение, но имеет более «тяжёлые» концы и больший коэффициент эксцесса.
Стохастический интеграл — интеграл вида  , где
, где  — случайный процесс с независимыми нормальными приращениями. Стохастические интегралы широко используются в стохастических дифференциальных уравнениях. Стохастический интеграл нельзя вычислять как обычный интеграл Стилтьеса.
— случайный процесс с независимыми нормальными приращениями. Стохастические интегралы широко используются в стохастических дифференциальных уравнениях. Стохастический интеграл нельзя вычислять как обычный интеграл Стилтьеса.
Постоянная Голомба — Дикмана — математическая константа, возникающая в случайных перестановках и в теории чисел, равная:
 .
.
Теорема Пуассона — теорема в теории вероятностей.
Криптосистема Пэйе — вероятностная криптосистема с открытым ключом, изобретенная французским криптографом Паскалем Пэйе в 1999 году. Аналогично криптосистемам RSA, Гольдвассера-Микали и Рабина, криптосистема Пэйе основана на сложности факторизации составного числа, являющегося произведением двух простых чисел.
Принцип максимума энтропии утверждает, что наиболее характерными распределениями вероятностей состояний неопределенной среды являются такие распределения, которые максимизируют выбранную меру неопределенности при заданной информации о «поведении» среды. Впервые подобный подход использовал Д.Гиббс для нахождения экстремальных функций распределений физических ансамблей частиц. Впоследствии Э.Джейнсом был предложен формализм восстановления неизвестных законов распределения случайных величин при наличии ограничений из условий максимума энтропии Шеннона.
 Функция вероятности
Функция вероятности 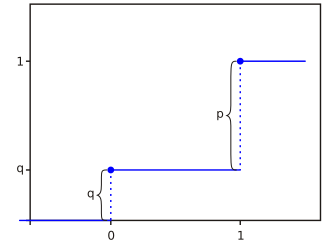 Функция распределения
Функция распределения 

























![{\displaystyle \mathbb {E} [X]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bff53623cf28729d4da4500f0618fd24380b0b)
![{\displaystyle \operatorname {D} [X]=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676350236a16d3c5d5d603eaf93da7b006fc3454)

![{\displaystyle \mathbb {E} \left[X^{n}\right]=\Pr(X=1)\cdot 1^{n}+\Pr(X=0)\cdot 0^{n}=p\cdot 1^{n}+q\cdot 0^{n}=p=\mathbb {E} [X],\forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9798a45d24eee884b4c9b48c1b79129d8132b4fc)




























