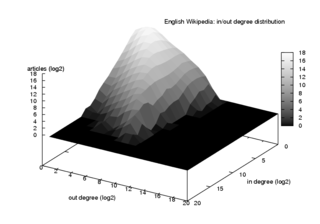
Сложные се́ти или комплексные сети — это существующие в природе сети (графы), обладающие нетривиальными топологическими свойствами.
Модель Барабаши-Альберт (БА) — алгоритм генерации случайных безмасштабных сетей с использованием принципа предпочтительного присоединения. Безмасштабные сети широко распространены в природных сетях и сетях, созданных человеком.
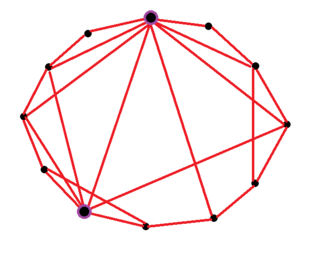
Граф «Мир тéсен» — разновидность графа, который имеет следующее свойство: если взять две произвольные вершины a и b, то они с большой вероятностью не являются смежными, однако одна достижима из другой посредством небольшого количества переходов через другие вершины. А именно, граф «Мир тесен» определяется как сеть, в которой типичное расстояние L между двумя произвольно выбранными вершинами растёт пропорционально логарифму от числа вершин N в сети, таким образом:

Проектная сеть — технологическая платформа, онлайн-сервис или веб-сайт, предназначенные для предоставления возможности самоорганизации участникам, обладающим ключевыми компетенциями, в проектную команду, для выполнения мероприятий с изначально установленными целями, достижение которых определяет завершение проекта.

k-Вырожденный граф — это неориентированный граф, в котором каждый подграф имеет вершины со степенью, не превосходящей k. Вырожденность графа — это наименьшее значение k, для которого граф является k-вырожденным. Вырожденность графа отражает, насколько граф разрежен и отражает другие меры разреженности, такие как древесность графа.
Биологические сети — любые сети, являющиеся частью биологических систем. Сеть — это любая система с подразделениями, которые связаны в единое целое, например, единичные виды, которые связаны в единую пищевую сеть. Биологические сети обеспечивают математическое представление связей, обнаруженных в результате экологических, эволюционных и физиологических исследований, таких как нервные сети. Анализ биологических сетей в отношении заболеваний человека привёл к появлению такой области, как сетевой медицины.

В статистике степенной закон — это такая функциональная зависимость между двумя величинами, при которой относительное изменение одной величины приводит к пропорциональному относительному изменению другой величины, независимо от исходных значений этих величин: зависимость одной величины от другой представляет собой степенную функцию. Например, рассмотрим зависимость площади квадрата от длины его стороны. Если длина будет увеличена вдвое, то площадь увеличится вчетверо.
Модель Эрдёша — Реньи — это одна из двух тесно связанных моделей генерации случайных графов. Модели названы именами математиков Пала Эрдёша и Альфреда Реньи, которые первыми представили одну из моделей в 1959 году, в то время как Эдгар Гильберт предложил другую модель одновременно и независимо от Эрдёша и Реньи. В модели Эрдёша и Реньи все графы с фиксированным набором вершин и фиксированным набором рёбер одинаково вероятны. В модели, предложенной Гильбертом, каждое ребро имеет фиксированную вероятность присутствия или отсутствия, независимую от других рёбер. Эти модели можно использовать в вероятностном методе для доказательства существования графов, удовлетворяющих различным свойствам или для обеспечения точного определения, это для свойства понимается, что оно выполняется для почти всех графов.

Степень посредничества — это мера центральности в графе, основанная на кратчайших путях. Для любой пары вершин в связном графе существует по меньшей мере один (кратчайший) путь между вершинами, для которого минимально либо число рёбер, по которым путь проходит,, либо сумма весов этих рёбер. Степень посредничества для каждой вершины равна числу этих кратчайших путей через вершину.

Показатель центральности или близости к центру в теории графов и анализе сетей определяет наиболее важные вершины графа. Приложения показателя применяются для выявления наиболее влиятельного лица (лиц) в социальной сети, ключевых узлов инфраструктуры в интернете или городских сетей и разносчиков болезни. Концепции центральности первоначально развивались в анализе социальных сетей и многие термины центральности используются для измерения социологических первоисточников. Не следует путать эти показатели с метриками влияния узлов, которые ищут количественные характеристики влияния каждого узла в сети.
Степень близости узла — это мера центральности в сети, вычисляемая как обратная величина суммы длин кратчайших путей между узлом и всеми другими узлами графа. Таким образом, чем более централен узел, тем ближе он ко всем другим узлам.

Наука о сетях — это научная область, которая изучает комплексные сети, такие как коммуникационные, компьютерные, биологические, когнитивные и семантические сети, а также социальные сети, и рассматривает различные элементы или участников процесса, представленных узлами, и связи между элементами или участниками, представленные связями. Эта научная область заимствует теории и методы из теории графов, статистической механики, интеллектуального анализа данных и визуализации информации из информатики, моделирование логического вывода из статистики и социальную структуру из социологии. Национальный научно-исследовательский совет США определяет науку о сетях как «изучение сетевых представлений физических, биологических и социальных явлений, ведущее к прогнозирующим моделям этих явлений».
Показатель влияния узла — это мера, которая ранжирует или количественно выражает влияние каждого узла в графе. Показатели имеют связь с индексами центральности. Приложения показателя включают меры влияния каждого лица в социальной сети, понимание роли узлов в транспортных сетях, интернете, или городских сетях и роль данного узла в динамике заболевания.

Модулярность — одна из мер структуры сетей или графов. Мера была разработана для измерения силы разбиения сети на модули. Сети с высокой модулярностью имеют плотные связи между узлами внутри модулей, но слабые связи между узлами в различных модулях. Модулярность часто используется в оптимизации методов для распознавания структуры сообщества в сетях. Однако было показано, что модулярность обладает проблемой пределов разрешающей способности, поэтому эта мера неспособна различить малые сообщества. Биологические сети, включая мозги животных, обнаруживают высокую степень модулярности.

Альберт-Ласло Барабаши — венгерско-американский физик румынского происхождения. Известен своими исследованиями в области теории сетей.

Квантовый точечный контакт (КТК) — узкое сужение между двумя широкими электропроводящими областями, ширина которого сопоставима с длиной волны электронов.

Ассортати́вность, или ассортативное смешивание — предпочтение узлов сети присоединяться к другим узлам, которые каким-либо образом похожи на них. Хотя конкретная мера сходства может различаться, теоретики сетей часто исследуют ассортативность в терминах степеней узла. Добавление этой характеристики в сетевые модели часто позволяет более точно аппроксимировать поведение многих реальных сетей.
В области комплексных сетей ассортативное смешивание, или ассортативность, — это смещение в пользу связей между узлами сети со схожими характеристиками. В конкретном случае социальных сетей ассортативное смешивание также известно как гомофилия. Более редкий термин дизассортативное смешивание обозначает смещение в пользу связей между несхожими узлами.
Паттерны смешивания относятся к систематическим тенденциям одного типа узлов какой-либо сети соединяться с другим типом. Например, узлы могут иметь тенденцию соединяться с другими узлами, которые очень похожи или очень отличаются. Эта особенность весьма распространена во многих социальных сетях, хотя также иногда наблюдается в не-социальных сетях. Паттерны смешивания тесно связаны с ассортативностью; однако, для целей данной статьи этот термин используется для обозначения ассортативного или дизассортативного смешивания, в зависимости от факторов реального мира, топологических или социологических.