Расстояние Фреше
Расстояние Фреше — это мера сходства кривых, принимающая во внимание число и порядок точек вдоль кривых. Расстояние названо по имени французского математика Мориса Фреше.
Интуитивное определение
Представьте себе человека, идущего по конечному криволинейному пути, выгуливающего свою собаку на поводке, причем собака пересекает отдельный конечный изогнутый путь. Каждый из них может изменять свою скорость, чтобы не ослаблять поводок, но ни один из них не может двигаться назад. Расстояние Фреше между двумя кривыми — это длина кратчайшего поводка, достаточная для того, чтобы оба могли пройти свои отдельные пути от начала до конца.
Обратите внимание, что определение симметрично относительно двух кривых: расстояние Фреше было бы таким же, если бы собака выгуливала своего хозяина.
Формальное определение
Пусть — метрическое пространство. Кривая в пространстве — это непрерывное отображение единичного отрезка в , т.е. . Репараметризация отрезка — это непрерывная неубывающая сюръекция .
Пусть и — две кривые в . Тогда расстояние Фреше между и определяется как точная нижняя граница по всем репараметризациям и отрезка по всем максимумам расстояний в между и . В математических обозначениях расстояние Фреше равно
,
где — функция расстояния пространства .
Неформально, мы можем считать параметр «временем». Тогда является положением собаки, а — положением владельца собаки по времени (или наоборот). Длина поводка между ними в момент времени равна расстоянию между и . Взятие инфимума по всем возможным репараметризациям отрезка соответствует выбору прогулки вдоль кривых, при которой максимальная длина поводка минимизируется. Ограничение, что и не убывают, означает, что ни собака, ни её владелец не могут повернуть назад.
Метрика Фреше принимает во внимание течение двух кривых, поскольку пары точек, расстояние между которыми определяет расстояние Фреше, «пробегают» вдоль кривых. Это делает расстояние Фреше лучшей мерой похожести кривых по сравнению с метрикой Хаусдорфа для произвольного множества точек. Две кривые могут иметь маленькое хаусдорфово расстояние, но большое расстояние Фреше.
Расстояние Фреше и его вариации находят применение в некоторых задачах, от морфинга[1] и распознавания рукописного ввода[2] до расположения протеиновых структур[3]. Альт и Годау[4] первыми описали алгоритм полиномиального времени для вычисления расстояния Фреше между двумя ломаными в евклидовом пространстве, основанном на принципах параметрического поиска[англ.]. Время работы их алгоритма равно для двух ломаных с m и n отрезками.
Диаграмма свободного пространства
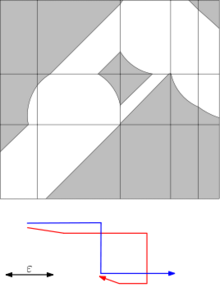
Важным средством вычисления расстояния Фреше между двумя кривыми является диаграмма свободного пространства, которую предложили Альт и Годау[4]. Диаграмма свободного пространства между двумя кривыми для заданного порога расстояния ε — это двумерная область в пространстве параметров, состоящая из всех пар точек двух кривых, находящихся на расстоянии, не превосходящем ε:
Расстояние Фреше не превосходит ε тогда и только тогда, когда диаграмма свободного пространства содержит путь из левого нижнего угла в правый верхний угол, монотонный как по горизонтали, так и по вертикали.
Варианты
Слабое расстояние Фреше — это вариант классического расстояния Фреше без требования монотонности движения вдоль кривых, собаке и её владельцу разрешается обратное движение. Альт и Годау[4] описали простой алгоритм для вычисления слабого расстояния Фреше между ломаными, основанном на вычислении минимаксного пути в связанной решётке.
Дискретное расстояние Фреше, называемое также сцепленным расстоянием, — это аппроксимация метрики Фреше для ломаных, определённая Айтером и Маннилой[5]. Дискретное расстояние Фреше рассматривает только положения поводка в вершинах двух ломаных и никогда внутри ребра. Эта специальная структура позволяет вычислить дискретное расстояние Фреше за полиномиальное время с помощью простого алгоритма динамического программирования.
Если две кривые вложены в метрическое пространство, отличное от евклидова, такое как многогранный рельеф[англ.], или вложены в евклидово пространство с препятствиями, расстояние между двумя точками на кривых естественно определить как длину кратчайшего пути между ними. Поводок в этом случае является геодезической, соединяющей две точки. Получившаяся метрика между кривыми называется геодезическим расстоянием Фреше[1][6][7]. Кук и Венк[6] описали алгоритм полиномиального времени вычисления геодезического расстояния Фреше между двумя ломаными в простом многоугольнике.
Если мы потребуем, чтобы поводок двигался непрерывно в окружающем метрическом пространстве, получим понятие гомотопное расстояние Фреше[8] между двумя кривыми. Поводок не может «перепрыгивать» с одной позиции в другую и, в частности, не может «перепрыгивать» через препятствия и может «перелезать» через горы, только будучи достаточно длинным. Движение поводка описывает гомотопия между двумя кривыми. Чамберс с соавторами[8] описал алгоритм полиномиального времени вычисления гомотопного расстояния Фреше между ломаными на евклидовой плоскости с препятствиями.
Примеры
Расстояние Фреше между двумя концентричными окружностями с радиусами и равно . Наибольший поводок нужен, когда владелец стоит, а собака бежит в противоположную точку окружности (), а наименьший поводок будет, когда владелец и собака движутся с одинаковой угловой скоростью вокруг окружности ().
Примечания
- ↑ 1 2 Efrat, Guibas, Har-Peled, Mitchell, Murali, 2002, с. 535–569.
- ↑ Sriraghavendra, Karthik, Bhattacharyya, 2007, с. 461–465.
- ↑ Minghui, Ying, Binhai, 2008, с. 51–64.
- ↑ 1 2 3 Alt, Godau, 1995, с. 75–91.
- ↑ Eiter, Mannila, 1994.
- ↑ 1 2 Cook, Wenk, 2008.
- ↑ Maheshwari, Yi, 2005, с. 41–44.
- ↑ 1 2 Chambers и др., 2009, с. 295–311.
Литература
- Alon Efrat, Leonidas J. Guibas, Sariel Har-Peled, Joseph S. B. Mitchell, T. M. Murali. New similarity measures between polylines with applications to morphing and polygon sweeping // Discrete and Computational Geometry. — 2002. — Т. 28, вып. 4. — С. 535—569. — doi:10.1007/s00454-002-2886-1.
- R. Sriraghavendra, K. Karthik, Chiranjib Bhattacharyya. Proc. 9th International Conference on Document Analysis and Recognition (ICDAR '07). — 2007. — С. 461—465. — doi:10.1109/ICDAR.2007.121.
- Jiang Minghui, Xu Ying, Zhu Binhai. Protein structure-structure alignment with discrete Fréchet distance // Journal of Bioinformatics and Computational Biology. — 2008. — Т. 6, вып. 1. — С. 51—64. — doi:10.1142/S0219720008003278. — PMID 18324745.
- Helmut Alt, Michael Godau. Computing the Fréchet distance between two polygonal curves // International Journal of Computational Geometry and Applications. — 1995. — Т. 5, вып. 1—2. — С. 75—91. — doi:10.1142/S0218195995000064.
- Thomas Eiter, Heikki Mannila. Computing discrete Fréchet distance. — Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria, 1994. — (Tech. Report CD-TR 94/64).
- Atlas F. Cook, Carola Wenk. Geodesic Fréchet distance with polygonal obstacles. — University of Texas at San Antonio, 2008. — (Tech. Report CS-TR-2008-0010).
- Anil Maheshwari, Jiehua Yi. Proc. 21st European Workshop on Computational Geometry. — 2005. — С. 41—44.
- Erin Wolf Chambers, Éric Colin de Verdière, Jeff Erickson, Sylvain Lazard, Francis Lazarus, Shripad Thite. Homotopic Fréchet distance between curves, or Walking your dog in the woods in polynomial time // Computational Geometry: Theory and Applications. — 2009. — Т. 43. — С. 295—311. — doi:10.1016/j.comgeo.2009.02.008. (недоступная ссылка)
Литература для дальнейшего чтения
- Mark de Berg. Computational Geometry, Two Selected Topics. — С. 11—75..
- Boris Aronov, Sariel Har-Peled, Christian Knauer, Yusu Wang, Carola Wenk. Proc. 14th European Symposium on Algorithms. — Springer-Verlag, 2006. — Т. 4168. — С. 52—63. — (Lecture Notes in Computer Science). — doi:10.1007/11841036_8..
- Helmut Alt, Maike Buchin. Can we compute the similarity between surfaces? // Discrete and Computational Geometry. — 2010. — Т. 43. — С. 78—99. — doi:10.1007/s00454-009-9152-8. — arXiv:cs.CG/0703011..


![{\displaystyle A:[0,1]\rightarrow S}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6edd4c77af36de6c609ab6800cce5f57c21742e)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle \alpha :[0,1]\rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3670292977d70d09aa06595f56abffe9173dfa8f)


![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)



![{\displaystyle F(A,B)=\inf _{\alpha ,\beta }\,\,\max _{t\in [0,1]}\,\,{\Bigg \{}d{\Big (}A(\alpha (t)),\,B(\beta (t)){\Big )}{\Bigg \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3395e48df64fa6870dcdc64f6992558789a2a1f7)



![{\displaystyle D_{\varepsilon }(A,B):=\{\,(\alpha ,\beta )\in [0,1]^{2}\mid d(A(\alpha ),B(\beta ))\leq \varepsilon \,\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5528eadf0a7d67fe052cdcf26a27b5a350b19b5)