
Диффу́зия — неравновесный процесс перемещения вещества из области с высокой концентрацией в область с низкой концентрацией, приводящий к самопроизвольному выравниванию концентраций по всему занимаемому объёму. Обычно рассматривают диффузию одного вещества в среде, но возможно и диффузия двух веществ, тогда говорят о взаимной диффузии газов. В плазме ионы и электроны имеют заряд и при взаимном проникновении одного вещества в другое вместо взаимной диффузии используют термин амбиполярная диффузия. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией против направления градиента концентрации.
Уравне́ние Шрёдингера — линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах.
Си́мплекс или n-ме́рный тетра́эдр — геометрическая фигура, являющаяся n-мерным обобщением треугольника.
Лагранжева механика — формулировка классической механики, введённая Луи Лагранжем в 1788 году. В лагранжевой механике траектория объекта получается при помощи отыскания пути, который минимизирует действие — интеграл от функции Лагранжа по времени. Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией.
Антидеси́ттеровское простра́нство — псевдориманово многообразие постоянной отрицательной кривизны. Его можно считать псевдоримановым аналогом  -мерного гиперболического пространства. Названо как противопоставление пространству де Ситтера, обозначается обычно
-мерного гиперболического пространства. Названо как противопоставление пространству де Ситтера, обозначается обычно  .
.
В этой статье рассматривается математический базис общей теории относительности.
Вселе́нная Фри́дмана — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
Уравнение Колмогорова — Чепмена для однопараметрического семейства непрерывных линейных операторов  в топологическом векторном пространстве выражает полугрупповое свойство:
в топологическом векторном пространстве выражает полугрупповое свойство:

Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие их физического подобия.
Ло́ренц-ковариа́нтность — свойство систем математических уравнений, описывающих физические законы, сохранять свой вид при применении преобразований Лоренца. Более точно, всякий физический закон должен представляться релятивистски инвариантной системой уравнений, то есть инвариантной относительно полной ортохронной неоднородной группы Лоренца. Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.
Фундаментальное решение линейного дифференциального оператора L или, эквивалентно, соответствующего ему линейного уравнения в частных производных — математическое понятие, обобщающее идею функции Грина для дифференциальных операторов, без связи с какой-либо областью и граничными условиями.
Тео́рия Бра́нса — Ди́кке — скалярно-тензорная теория гравитации, совпадающая в одном из пределов с общей теорией относительности. В теории Йордана — Бранса — Дикке как скалярно-тензорной метрической теории гравитационное воздействие на материю реализуется через метрический тензор пространства-времени, а материя влияет на метрику не только непосредственно, но и через генерируемое дополнительно скалярное поле  . Из-за этого в теории Йордана — Бранса — Дикке гравитационная постоянная G не обязательно постоянна, но зависит от скалярного поля
. Из-за этого в теории Йордана — Бранса — Дикке гравитационная постоянная G не обязательно постоянна, но зависит от скалярного поля  , которое может изменяться в пространстве и времени.
, которое может изменяться в пространстве и времени.

Статистическая механика или статистическая термодинамика — механика больших ансамблей относительно простых систем, таких как атомы в кристалле, молекулы в газе, фотоны в лазерном пучке, звёзды в галактике, автомобили на шоссе. Статистическая механика использует статистические методы для определения свойств и поведения макроскопических физических систем, находящихся в термодинамическом равновесии, на основе их микроскопической структуры и законов движения, которые считаются заданными. Статистические методы были введены в этом контексте Максвеллом в серии из трех статей (1860—1879) и Больцманом в серии из четырёх статей (1870—1884), которые заложили основы кинетической теории газов. Классическая статистическая механика была основана Гиббсом (1902); а позднее описание микроскопических состояний на основе классической механики было исправлено и дополнено в соответствии с квантовой механикой. Термодинамика, кинетическая теория и статистическая механика — это дисциплины, связанные объектом исследования, но отличающиеся используемыми методами; часто они представлены вместе под общим названием статистической физики. Последовательное построение неравновесной статистической механики было выполнено Н. Н. Боголюбовым в 1946 году. При описании систем в рамках статистической механики используется понятие среднего по ансамблю. Основными уравнениями статистической механики являются уравнения Лиувилля и цепочка уравнений Боголюбова.
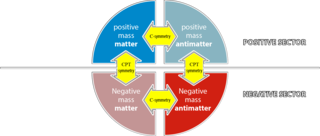
Биметрические теория гравитации — альтернативные теории гравитации, в которых вместо одного метрического тензора используются два или более. Часто вторая метрика вводится только при высоких энергиях, в предположении, что скорость света может зависеть от энергии. Наиболее известными примерами биметрических теорий являются теория Розена и релятивистская теория гравитации.
Пропагатор в квантовой механике и квантовой теории поля (КТП) — функция, характеризующая распространение релятивистского поля от одного акта взаимодействия до другого. Эта функция определяет амплитуду вероятности перемещения частицы из одного места пространства в другое за заданный промежуток времени или перемещения частицы с определённой энергией и импульсом. Для расчёта частоты столкновений в КТП используются виртуальные частицы, представленные в диаграммах Фейнмана пропагаторами, вносят свой вклад в вероятность рассеяния, описываемого соответствующей диаграммой. Их также можно рассматривать как оператор, обратный волновому оператору, соответствующему частице, и поэтому их часто называют (причинными) функциями Грина.
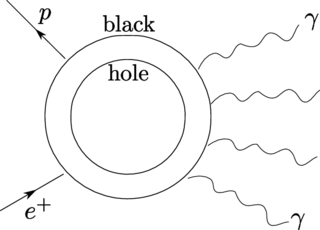
Виртуальная чёрная дыра — гипотетический объект квантовой гравитации: чёрная дыра, возникшая в результате квантовой флуктуации пространства-времени. Является одним из примеров так называемой квантовой пены и гравитационным аналогом виртуальных электрон-позитронных пар в квантовой электродинамике.
Функция Гильберта, ряд Гильберта и многочлен Гильберта градуированной коммутативной алгебры, конечно порождённой над полем — это три тесно связанных понятия, которые позволяют измерить рост размерности однородных компонент алгебры.

Специальная теория относительности (СТО) описывает пространство-время в виде псевдориманова многообразия с одним отрицательным собственным значением метрического тензора, которое соответствует «временноподобному» направлению. Метрика с несколькими отрицательными собственными значениями будет соответственно подразумевать наличие нескольких временных направлений, то есть время будет многомерным, но в настоящее время нет консенсуса насчёт связи этих дополнительных «времён» с временем в обычном понимании.
Информационная метрика Фишера в информационной геометрии — это особая риманова метрика, которая может быть определена на гладком статистическом многообразии, то есть на гладком многообразии, точки которого являются вероятностными мерами из общего вероятностного пространства. Ее можно использовать для расчета информационной разницы между измерениями.

![{\displaystyle {\text{d}}s^{2}=-{\text{d}}t^{2}+\sum _{j=1}^{D-1}t^{2p_{j}}[{\text{d}}x^{j}]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7613446822d0efd7919a5e3d32a9b9071d189d91)

















