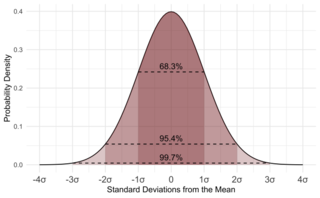
Стати́стика — отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме.

Матема́тика — точная формальная наука, первоначально исследовавшая количественные отношения и пространственные формы. В более современном понимании, это наука об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, — именно тех, которые в качестве аксиом положены в основание той или иной математической теории.

Прикладна́я матема́тика — область математики, рассматривающая применение математических методов, алгоритмов в других областях науки и техники. Примерами такого применения будут: численные методы, математическая физика, линейное программирование, оптимизация и исследование операций, моделирование сплошных сред, биоматематика и биоинформатика, теория информации, теория игр, теория вероятностей и статистика, финансовая математика и актуарные расчёты, криптография, а следовательно комбинаторика и в некоторой степени конечная геометрия, теория графов в приложении к сетевому планированию, и во многом то, что называется информатикой. В вопросе о том, что является прикладной математикой, нельзя составить чёткую логическую классификацию. Математические методы обычно применяются к специфическому классу прикладных задач путём составления математической модели.

Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.
Математи́ческий ана́лиз — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное и интегральное исчисления.

Биоинформа́тика — междисциплинарная область, объединяющая общую биологию, молекулярную биологию, кибернетику, генетику, химию, компьютерные науки, математику и статистику. Крупномасштабные биологические проблемы, требующие анализа больших объёмов данных, решаются биоинформатикой с вычислительной точки зрения. Биоинформатика главным образом включает в себя изучение и разработку компьютерных методов и направлена на получение, анализ, хранение, организацию и визуализацию биологических данных.

Тео́рия игр — математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более стороны, ведущие борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.

Данная статья представляет собой обзор основных событий и тенденций в истории математики с древнейших времён до наших дней.
Динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.

Аполло́ний Пергский — древнегреческий математик, один из трёх великих геометров античности, живших в III веке до н. э.
Математи́ческая моде́ль — математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе. Математическая модель, в частности, предназначена для прогнозирования поведения реального объекта, но всегда представляет собой ту или иную степень его идеализации.

Оптимизация — задача нахождения экстремума целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств или неравенств.
Игра — тип олимпиадных задач по математике, в которых требуется проанализировать стратегию игры и/или назвать победителя этой игры. Обычно заканчивается традиционным вопросом: «Кто выиграет при правильной игре?»
Машинное обучение — класс методов искусственного интеллекта, характерной чертой которых является не прямое решение задачи, а обучение за счёт применения решений множества сходных задач. Для построения таких методов используются средства математической статистики, численных методов, математического анализа, методов оптимизации, теории вероятностей, теории графов, различные техники работы с данными в цифровой форме.
Шансы — термин, использующийся игроками в покер для определения математического ожидания хода в игре. Шансы обычно указываются в форме отношения ожидаемого количества побед к количеству поражений, например, 1:4, именно таким форматом будем пользоваться далее. Иногда также используется обратная пропорция — шансы против улучшения, то есть отношение поражений к победам — 4:1. Шансы можно перевести в вероятность наступления события по формуле: кол-во побед/(кол-во побед + кол-во поражений). Таким образом, шансам 1:4 соответствует вероятность 1/(1+4)=1/5.
Задача Бертрана — задача, обратная к задаче двух тел и состоящая в определении силы взаимодействия по известным свойствам траекторий движения.
Кенгуру, официальное международное название Международный Математический Кенгуру или «Кенгуру без границ» — международный математический конкурс-игра для школьников.
Основнóй государственный экзáмен (ОГЭ) — итоговый экзамен за курс основного общего образования в России. Служит для контроля знаний, полученных учащимися за 9 лет, а также для приёма в учреждения среднего профессионального образования. Является одной из трёх форм Государственной итоговой аттестации (ГИА).
Детерминированный алгоритм — алгоритмический процесс, который выдаёт уникальный и предопределённый результат для заданных входных данных.

История теории вероятностей отмечена многими уникальными особенностями. Прежде всего, в отличие от появившихся примерно в то же время других разделов математики, у теории вероятностей по существу не было античных или средневековых предшественников, она целиком — создание Нового времени. Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой», её строгое обоснование было разработано только в 1929 году, то есть даже позже, чем аксиоматика теории множеств (1922). В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения; «нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы».










