Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с элементами симметрии.

Трикли́нная сингони́я — одна из семи сингоний в кристаллографии. Её элементарная ячейка определяется тремя базовыми векторами (трансляциями) разной длины, все углы между которыми не являются прямыми. Таким образом, форма ячейки определяется шестью параметрами: длинами базовых векторов a, b и c и углами между ними α, β и γ. Объём ячейки равен 

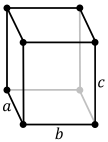
Монокли́нная сингони́я — в кристаллографии одна из семи сингоний. Элементарная ячейка моноклинной сингонии строится на трёх векторах a, b и c, имеющих разную длину, с двумя прямыми и одним непрямым углами между ними. Таким образом, форма ячейки определяется четырьмя параметрами: длинами базовых векторов a, b и c и углом β, отличающимся от прямого угла. Объём ячейки равен произведению 
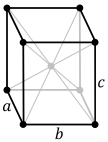
Решётка Браве́ — понятие для характеристики кристаллической решётки относительно сдвигов. Названа в честь французского физика Огюста Браве. Решёткой или системой трансляций Браве называется набор элементарных трансляций или трансляционная группа, которыми может быть получена вся бесконечная кристаллическая решётка. Все кристаллические структуры описываются 14 решётками Браве, число которых ограничивается симметрией.

В кристаллографии куби́ческая сингони́я — одна из семи сингоний. Элементарная ячейка кристалла кубической сингонии определяется тремя векторами равной длины a, перпендикулярными друг другу. Объём ячейки равен a3.

Тригона́льная сингони́я — одна из семи сингоний в кристаллографии. Элементарная ячейка определяется тремя базовыми векторами одинаковой длины, с равными, но не прямыми, углами между векторами; таким образом, форма ячейки определяется двумя параметрами: длиной базового вектора a и углом между базовыми векторами β. Объём ячейки равен 
Тетрагона́льная cингони́я — одна из семи cингоний в кристаллографии. Элементарная ячейка определяется тремя базовыми векторами; два из трёх базовых векторов имеют одинаковую длину, а третий отличается от них. Все три вектора перпендикулярны друг другу. Таким образом, форма ячейки определяется двумя параметрами: длинами базовых векторов a и c. Объём ячейки равен a2c.

Сингони́я — классификация кристаллографических групп симметрии, кристаллов и кристаллических решёток в зависимости от системы координат ; группы симметрии с единой координатной системой объединяются в одну сингонию. Кристаллы, принадлежащие к одной и той же сингонии, имеют подобные углы и рёбра элементарных ячеек.
Кристаллографическая группа — дискретная группа движений  -мерного евклидова пространства, имеющая ограниченную фундаментальную область.
-мерного евклидова пространства, имеющая ограниченную фундаментальную область.

Ромбоэдр — это геометрическое тело, являющееся обобщением куба, у которого грани не обязательно квадратны, а лишь являются ромбами. Ромбоэдр является параллелепипедом, в котором все рёбра равны. Ромбоэдр можно использовать для определения ромбоэдрической решётчатой системы, сот с ромбоэдрическими ячейками.
Кристаллогра́фия — наука о кристаллах, их структуре, возникновении и свойствах. Она тесно связана с минералогией, физикой твёрдого тела и химией. Исторически кристаллография возникла в рамках минералогии, как наука, описывающая идеальные кристаллы.

Постоя́нная решётки, или параметр решётки — размеры элементарной кристаллической ячейки кристалла. В общем случае элементарная ячейка представляет собой параллелепипед с различными длинами рёбер, обычно эти длины обозначают как a, b, c. Но в некоторых частных случаях кристаллической структуры дли́ны этих рёбер совпадают. Если к тому же выходящие из одной вершины рёбра равны и взаимно перпендикулярны, то такую структуру называют кубической. Структуру с двумя равными рёбрами, находящимися под углом 120 градусов, и третьим ребром, перпендикулярным им, называют гексагональной.

Элементарная ячейка — в геометрии, физике твёрдого тела и минералогии, в частности при обсуждении кристаллической решётки, минимальная ячейка, отвечающая единичной решёточной точке структуры с трансляционной симметрией в 2D, 3D или других размерностях.
Кристаллографические группы, или фёдоровские группы — набор групп симметрий, которые описывают все возможные симметрии бесконечного количества периодически расположенных точек в трёхмерном пространстве. Эта классификация симметрий была сделана независимо и почти одновременно русским математиком Фёдоровым и немецким математиком Шёнфлисом. Полученные сведения играют большую роль в кристаллографии.
Символы Германа — Могена используются для обозначения симметрии точечных групп, плоских групп и пространственных групп. Были предложены немецким кристаллографом Карлом Германом в 1928 году и модифицированы французским минералогом Шарлем-Виктором Могеном в 1931 году. Также называются международными символами, поскольку используются в Интернациональных Таблицах по Кристаллографии, начиная с их первого издания в 1935 году. До этого для обозначения точечных и пространственных групп пользовались, как правило, символами Шёнфлиса.

Стефанит — минерал из класса сульфосолей, открыт в 1845 году. Назван в честь эрцгерцога австрийского Стефана Франца Виктора Габсбурга-Лотарингского (1817—1867), который собрал выдающуюся коллекцию минералов из 20 тысяч образцов. Из свойств можно отметить разложение разбавленной азотной кислотой с выделением S и Sb2S3, легкоплавкость и образование тёмного налёта под действием света. Стефанит также называли кислым серебром, ломким серебром и чёрным серебром.

Группа орнамента — это математическая классификация двумерных повторяющихся узоров, основанных на симметриях. Такие узоры часто встречаются в архитектуре и декоративном искусстве. Существует 17 возможных различных групп.
Симметрии в квантовой механике — преобразования пространства-времени и частиц, которые оставляют неизменными уравнения квантовой механики. Рассматриваются во многих разделах квантовой механики, которые включают релятивистскую квантовую механику, квантовую теорию поля, стандартную модель и физику конденсированного состояния. В целом, симметрия в физике, законы инвариантности и сохранения являются основополагающими ограничениями для формулирования физических теорий и моделей. На практике это мощные методы решения задач и прогнозирования того, что может случиться. Хотя законы сохранения не всегда дают конечное решение проблемы, но они формируют правильные ограничения и наметки к решению множества задач.

Молекулярная симметрия — это фундаментальная концепция химии, описывающая и классифицирующая симметрию молекулы, используемая для предсказания или объяснения химических свойств молекул. Например, таких как дипольный момент и разрешённые спектроскопические переходы. Изучение молекулярной симметрии основано на теории групп. Состояние молекулы классифицируется с помощью неприводимых представлений из таблицы характеров группы симметрии молекулы.