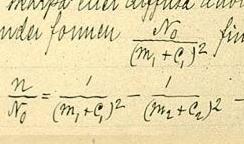Сверхтонкая структура

Сверхто́нкая структу́ра — расщепление спектральных линий вследствие взаимодействия электронной оболочки атомов со спином ядра, а также вследствие существования различных изотопов элементов, отличающихся массой и магнитным моментом ядра.
Объяснение происхождения (из-за спина ядра) этих линий предложил Вольфганг Паули.
Исследование сверхтонкой структуры спектральных линий можно использовать для определения спина ядра, например, для одного стабильного изотопа натрия он равен 3/2 (в единицах постоянной Планка).
Сверхтонкая структура энергетических уровней атома цезия используется в современном определении единицы времени — секунды.
История
Первые исследования сверхтонкой структуры проводились ещё в XIX веке: В 1891 году Майкельсон наблюдал её с помощью своего интерферометра. В 1897 году её описывали Фабри и Перо[1], а позже — Люммер и Герке[англ.][2]. Оказалось, что каждая спектральная линия на самом деле состоит из многих (до 10 и более) близко расположенных компонент.
Параллельно с этим, в 1910 году были открыты изотопы радиоактивных элементов, а в 1912 году — и стабильных элементов. В 1918 году Аронберг смог экспериментально обнаружить изотопический сдвиг, сравнивая излучения двух образцов свинца[3].
В 1924 году Паули предположил, что расщепление спектральных линий связано с взаимодействием магнитных моментов атомного ядра и орбитальных электронов[1].
В 1925 году Гаудсмит и Уленбек открыли спин электрона, благодаря чему в 1927—1928 годах Бак и Гаудсмит смогли теоретически интерпретировать полученные к тому времени экспериментальные данные. В течение следующих трёх лет их результаты дополнялись и уточнялись многими учёными: в этом направлении работали Ферми, Бэчер, Казимир, Гаргривз и другие[4]. Большое значение для объяснения этого явления имели точные наблюдения сверхтонкой структуры дублета жёлтой D-линии натрия, которые провели 1928 году А. М. Теренин и Л. М. Добрецов.
С начала 30-х годов начала активно исследоваться сверхтонкая структура, и с её помощью были определены спины многих ядер. В 1932 году был открыт нейтрон, что позволило решить некоторые разногласия между экспериментальными и теоретическими данными (в первую очередь это касается измерений спина ядер азота−14, который оказался равным единице, однако, исходя из популярной в те годы протон-электронной модели ядра, он должен был быть полуцелым — это противоречие получила название «азотная катастрофа»[5]).
В 1945 году голландский астроном ван де Хюлст предсказал существование радиолинии излучения атома водорода длиной 21 см, которая образуется благодаря переходу между двумя уровнями сверхтонкой структуры[6]. В 1949 году И. С. Шкловский теоретически показал, что интенсивность этого излучения от межзвёздных облаков водорода достаточна для её наблюдения, а в 1951 году излучение было открыто экспериментально. Открытие этого излучения стало важной вехой в развитии радиоастрономии.
Благодаря точному теоретическому описанию сверхтонкого расщепления, Лэмб и Ризерфорд в 1947 году показали, что линии реальных спектров сдвинуты относительно теоретических. Это смещение, получившее название лэмбовский сдвиг, оказалось связанным с квантовыми флуктуациями вакуума. Открытие этого явления стало толчком для создания квантовой электродинамики[7].
С 1967 года эталон секунды определяется точно как 9 192 631 770 периодов излучения, соответствующего переходу между двумя уровнями сверхтонкой структуры атома цезия-133[8].
Механизмы возникновения сверхтонкой структуры
Существует несколько независимых причин для расщепления спектральных линий, которые объединяются и делают картину спектра достаточно сложной.
Изотопный сдвиг
Взаимодействие между электроном и ядром определяется, в первую очередь, их электрическим зарядом, который одинаков для различных изотопов. Однако, электрон вращается не вокруг ядра, а вокруг центра масс системы «ядро-электрон», расположение которого зависит от массы ядра. Смещение же энергетического уровня, вызванное конечной массой ядра, равно , где — энергия уровня при бесконечно массивном ядре. Благодаря расщеплению (при регистрации излучения от смеси изотопов) такого типа, каждая спектральная линия распадается на несколько линий, в соответствии с количеством изотопов элемента. Расстояние между энергетическими уровнями для различных изотопов в таком случае равно .
Кроме того, существует так называемый «специфический эффект массы», который возникает, когда вокруг ядра движется много электронов и связан с обменным взаимодействием. В силу принципа Паули движение электронов вокруг ядра не является независимым, а наоборот — волновые функции отдельных электронов связаны между собой. Волновая функция антисимметрична, что приводит к дополнительному вкладу к энергии взаимодействия с ядром.
Впрочем, эта схема объясняет лишь расщепление линий элементов с малой и средней атомной массой. Для тяжелых ядер этот эффект должен создавать очень малые сдвиги, которыми можно пренебречь, тогда как эксперименты, наоборот, показывали, что для тяжелых ядер изотопный сдвиг очень заметен.
Такое смещение обусловлено объемным эффектом. Упрощенно его можно объяснить так: закон Кулона справедлив лишь для точечных зарядов. Реальные же ядра имеют ненулевые размеры, которые растут приблизительно пропорционально кубическому корню из количества нуклонов в нём. И если снаружи ядра потенциал будет кулоновским, то внутри ядра электрическое взаимодействие ослабевает. Согласно положениям квантовой механики, электрон находится не на какой-то конкретной орбите, а с разной плотностью вероятности может находиться в разных областях около атома и, в частности, — в его ядре. При увеличении размеров ядра, вероятность, что электрон будет находиться внутри него, растет, а энергия связи, соответственно, уменьшается[3]. Поэтому для тяжелых ядер существенной вклад в расщепление вносит изменение их геометрических размеров[9].
Взаимодействие магнитных моментов
Магнитный дипольный момент ядра зависит от орбитальных и спиновых моментов нуклонов следующим образом:
| p | n | |
|---|---|---|
| g l | 1 | 0 |
| g s | 5,5855 | -3,82629 |
- где — масса нуклона;
- — число нуклонов в ядре;
- — орбитальное и спиновое гиромагнитные отношения, значения которых представлены в таблице[10].
Величину называют ядерный магнетон, и она является естественной единицей измерения магнитного момента ядра, поскольку максимальная проекция магнитного момента на некоторую ось всегда пропорциональна ядерном магнетону. По значению ядерный магнетон в (то есть, в 1836 раз) меньше магнетона Бора, и поэтому магнитные моменты ядер также примерно на три порядка меньше магнитных моментов электронов.
Если ядро атома обладает угловым моментом а электрон — полным угловым моментом (равный сумме орбитального углового момента и спинового), то их совокупный угловой момент в зависимости от их взаимного расположения может принимать все целые значения в диапазоне от до
Соответственно, меняется и энергия взаимодействия моментов ядра и электронной оболочки, которую можно приближенно представить как . Качественно это выражается в том, что каждый энергетический уровень электрона, которому соответствует спектральная линия, разделяется на или подуровней (соответственно, если больше , или наоборот). Исходя из того, что взаимодействие между магнитными моментами пропорционально косинусу угла между их направлениями, величину этого расщепления можно оценить как:
- где — величина магнитного поля электронов в области ядра, зависит от и других квантовых чисел;
- — магнитный момент ядра[11].
Максимальное расстояние между линиями, таким образом, равно:
- если или
- если
Правила отбора определяют, с которой подорбитали на которую может перейти электрон, а значит и какую энергию он может при этом высвободить (или поглотить). Одно из правил определяет возможные варианты изменения кроме случая
По величине сверхтонкое расщепление на три порядка меньше расстояния между компонентами тонкой структуры спектральных линий и для основного состояния составляет несколько гигагерц. Для возбуждённых состояний сверхтонкое расщепление уменьшается обратно пропорционально энергии связи возбуждённого электрона в степени 3/2[12].
Взаимодействие с квадрупольным электрическим моментом
Электрический дипольный момент ядра равен нулю в основном состоянии, из-за чётности квадрата волновой функции ядра[13], однако ядро (если оно не сферически симметричное) имеет квадрупольный момент, взаимодействие с которым приводит к дополнительному расщеплению спектральных линий[14]. Квадрупольные расщепления значительно меньше расщепления, связанного с магнитным взаимодействием.
Значение
Определение спина ядра с помощью анализа сверхтонкой структуры
При изучение сверхтонкой структуры спектра позволяет легко измерить спин ядра — в этом случае, достаточно просто подсчитать количество линий, на которые распадается спектральная линия: оно будет равным
В случае, когда известны более сложные способы вычислить спин ядра.
Правило интервалов
Подуровни энергетического уровня, которым соответствуют спектральные линии сверхтонкого расщепления характеризуются одними и теми же квантовыми числами и однако различными Расстояние между подуровнями, которым соответствуют квантовые числа и в таком случае, пропорционально Таким образом, расстояния между линиями сверхтонкой структуры относятся между собой как
Определив таким образом все значения, которые может принимать спин ядра можно определить исходя из того, что максимальное значение [15].
Сравнение интенсивностей линий
Во внешнем магнитном поле поведение атома определяется суммарным моментом а не отдельными моментами электронов и ядра, атом может ориентироваться в нём различными способами (проекция вектора будет принимать значения, соответственно от до ). Соответственно, вырожденность энергетического подуровня также будет равняться что, при равенстве других условий, приводит к тому, что интенсивности линий сверхтонкой структуры также будут относиться в той же пропорции. Сравнивая эти интенсивности можно установить [16].
Этот метод оказывается менее точным, чем правило интервалов, а потому имеет смысл только когда количество линий в сверхтонкой структуре некоторого энергетического уровня меньше трех. Такой случай характерен для щелочных металлов, например, натрия.
Использование в радиоастрономии
Основной уровень энергии водорода расщепляется на два близких подуровня, в зависимости от того, параллельными или антипараллельными являются направления спинов ядра и электрона основного состояния атома водорода. При переходе между этими уровнями излучается фотон с частотой 1420,4 МГц, что соответствует длине волны 21,1 см. Время спонтанного перехода с верхнего уровня на нижний для изолированного атома водорода (время жизни возбуждённого состояния) является значительным — около 1,1·107 лет[6]. Энергия для обратного перехода соответствует температуре лишь 0,068 К, поэтому такой переход происходит при столкновениях атомов водорода между собой даже в очень холодных облаках атомарного межзвёздного водорода или с фотонами реликтового излучения. Как результат, в облаках межзвездного нейтрального водорода устанавливается динамическое равновесие между атомами находящимися в возбуждённом и невозбуждённом состояниях.
Хотя плотность энергии такого излучения на единицу объёма очень незначительна, благодаря распространенности водорода в межзвёздном пространстве Вселенной, исследования излучения на этой частоте дает важную информацию о распределении вещества (водорода) в космосе.
Генераторы частоты
Благодаря высокой точности и стабильности, переходы между уровнями сверхтонкой структуры применяются для очень точного измерения времени. Распространенным вариантом является водородный генератор частоты, который использует описанный выше переход между уровнями сверхтонкой структуры водорода в слабом магнитном поле, во время которого испускается электромагнитное излучение с длиной волны 21,1 см. Для того, чтобы атомы быстро переходили в нижнее энергетическое состояние, пучок атомарного водорода в возбуждённом состоянии направляют в объемный резонатор, настроенный на соответствующую частоту излучения[17].
Сложности экспериментального исследования
Несмотря на очень малое расстояние между линиями, разрешения даже простых интерферометров, таких как интерферометр Фабри — Перо достаточно для их разделения. Главной сложностью при этом является ширина самих линий. Доплеровское уширение, обусловленное эффектом Доплера атомов из-за их теплового движения, делает ширину линий больше, чем расстояние между ними[18]. Так, например, для полного разрешения сверхтонкого расщепления линий натрия его нужно охладить до 5 K, что практически трудно реализовать — ведь эти атомы постоянно возбуждаются светом. Для решения этой проблемы можно использовать пучки быстрых атомов, движущихся перпендикулярно направлению луча наблюдения. Для более тяжелых атомов скорости теплового движения меньше, поэтому для возбуждения излучения может использоваться обычный тлеющий разряд.
Примечания
- ↑ 1 2 Advances in Quantum Chemistry, 1965, p. 47.
- ↑ Сивухин, 1986, p. 36.
- ↑ 1 2 ИЗОТОПИЧЕСКИЙ ЭФФЕКТ В АТОМНЫХ СПЕКТРАХ Архивная копия от 8 августа 2017 на Wayback Machine (рус.)
- ↑ Advances in Quantum Chemistry, 1965, p. 48.
- ↑ Відкриття — нейтрон. Дата обращения: 8 декабря 2020. Архивировано из оригинала 1 сентября 2017 года.
- ↑ 1 2 Радиолиния водорода 21 см Архивная копия от 1 октября 2020 на Wayback Machine (рус.)
- ↑ лэмбовский сдвиг Архивная копия от 14 июля 2017 на Wayback Machine (рус.)
- ↑ В ПОГОНЕ ЗА ТОЧНОСТЬЮ: ЕДИНЫЙ ЭТАЛОН ВРЕМЕНИ — ЧАСТОТЫ — ДЛИНЫ Архивная копия от 13 февраля 2019 на Wayback Machine (рус.)
- ↑ Путилов, Фабрикант, 1963, p. 323.
- ↑ Магнитный дипольный момент ядра Архивная копия от 24 июня 2017 на Wayback Machine (рус.)
- ↑ СВЕРХТОНКАЯ СТРУКТУРА И АТОМНОЕ ЯДРО Архивная копия от 10 августа 2017 на Wayback Machine (рус.)
- ↑ сверхтонкая структура Архивная копия от 9 июля 2017 на Wayback Machine (рус.)
- ↑ Варламов, Гончарова, Ишханов, 2010, p. 28.
- ↑ Ландау, Лифшиц, 1989, p. 579.
- ↑ Сивухин, 1986, p. 42.
- ↑ Сивухин, 1986, p. 43.
- ↑ водородный генератор Архивная копия от 16 июля 2019 на Wayback Machine (рус.)
- ↑ Сивухин, 1986, p. 37.
Литература
- Advances in Quantum Chemistry / Per-Olov Löwdin. — Нью-Йорк: Academic Press Inc, 1965. — Т. 2. — 371 с. — ISBN 978-008-058-227-6.
- Путилов К. А., Фабрикант В. А. Оптика, атомная физика, ядерная физика. // Курс физики.. — Друге. — М.: Государственное издательство физико-математической литературы, 1963. — Т. III. — 634 с.
- Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). // Теоретическая физика; Учеб. пособие для вузов.. — 4. — М.: Наука, 1989. — Т. III. — 768 с. — ISBN 5-02-014421-5.
- Сивухин Д. В. Часть 1. Атомная физика // Общий курс физики. — М.: Наука, 1986. — Т. V. Атомная и ядерная физика. — 426 с. — ISBN 5-02-014053-8.
- Варламов В. В., Гончарова Н. Г., Ишханов Б. С. Физика ядра и банки ядерных данных. — М.: Университетская книга, 2010. — 246 с. — ISBN 978-5-91304-106-7.