Свёртка (математический анализ)
Свёртка, конволюция — операция в функциональном анализе, которая при применении к двум функциям и возвращает третью функцию, соответствующую взаимнокорреляционной функции и . Операцию свёртки можно интерпретировать как «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на произвольных измеримых пространствах, и может рассматриваться как особый вид интегрального преобразования. В дискретном случае свёртка соответствует сумме значений с коэффициентами, соответствующими смещённым значениям , то есть


Определение
Пусть — две функции, интегрируемые относительно меры Лебега на пространстве . Тогда их свёрткой называется функция , определённая формулой
В частности, при формула принимает вид
Свёртка определена при почти всех и интегрируема.
В случае, когда , а функции определены на промежутке , свёртку можно записать в виде
Впервые интегралы, являющиеся свёрткой двух функций, встречаются в трудах Леонарда Эйлера (1760-е годы); позднее свёртка появляется у Лапласа, Лакруа, Фурье, Коши, Пуассона и других математиков. Обозначение свёртки функций при помощи звёздочки впервые предложил Вито Вольтерра в 1912 году на своих лекциях в Сорбонне (опубликованы годом позже)[1].
Свойства
- .
- .
Линейность (дистрибутивность по сложению и ассоциативность с умножением на скаляр):
- ,
- ,
- .
Правило дифференцирования:
- ,
где обозначает производную функции по любой переменной.
- .
Свойство фурье-образа:
- ,
где обозначает преобразование Фурье функции.
Если является матрицей дискретного преобразования Фурье, то:
- ,
где — символ торцевого произведения матриц[2][3][4][5][6], обозначает произведение Кронекера, — символ произведения Адамара (тождество является следствием свойств отсчётного скетча[7]).
Пример

Пусть стоит задача вычислить, как будет изменяться количество снега на каком-либо участке земли в зависимости от времени. Решение этой задачи можно разделить на два этапа:
- построить модель выпадения снега и модель таяния снега.
- каким-то образом соединить эти две модели в одну.
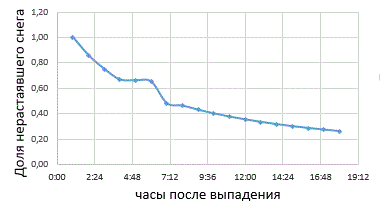
График зависимости количества нерастаявшего снега от времени прошедшего с момента его выпадения.
Задачи первого этапа решаются путём наблюдений и опытов, а задачи второго этапа — свёрткой получившихся на первом этапе моделей.
Пусть в результате решения задачи на первом этапе было построено две зависимости (математические модели):
- зависимость количества выпавшего снега от текущего времени ,
- зависимость доли нерастаявшего снега от времени, прошедшего с момента его выпадения .
Если бы снег не начинал таять, количество всех выпавших осадков можно было бы посчитать путём сложения в дискретном случае:
- ,
или путём интегрирования в случае непрерывном:
- .
Но в данном случае таяние снега имеет место и, более того, оно зависит не только от текущего общего количества снега, но и от того, в какой момент времени выпал этот конкретный объём снега. Так снег, выпавший две недели назад, может уже испариться, в то время как снег, выпавший полчаса назад, ещё будет лежать и даже не начнёт подтаивать.
Получается, что для снега, выпавшего в разное время, нужно построить свою модель таяния и как-то сложить все эти модели вместе.
Для этих целей и можно использовать понятие математической свёртки. Пусть в момент времени рассматривается снег, который выпал в момент времени , тогда
- — время выпадения снега. Например, 13:00;
- — количество выпавшего в момент снега. Например, 7 кг;
- — момент времени, для которого нам нужно узнать состояние выпавшего в снега. Например, 15:00;
- — количество времени, прошедшее с момента выпадения до момента расчёта оставшейся доли снега. То есть 15:00 − 13:00;
- — доля снега, которая не растаяла после того, как пролежала часов.
Нужно для каждого количества снега, выпавшего в момент времени , сложить множество моделей в одну функцию. Если это сделать, получится сумма в дискретном случае:
или интеграл в непрерывном:
Графически функция изображена ниже, где разными цветами представлены вклады каждой кучи снега из графика .
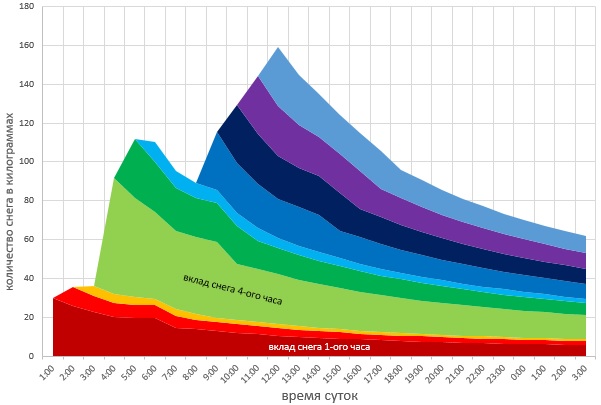
Функция полностью моделирует поведение снега, выпавшего согласно модели . Так, на графике выше видно, что общее количество снега увеличивается тремя скачками, но снег начинает таять сразу, не дожидаясь выпадения других осадков.
Свёртка на группах
Пусть — группа, оснащённая мерой , и — две функции, определённые на . Тогда их свёрткой называется функция[]
Свёртка мер
Пусть есть борелевское пространство и две меры . Тогда их свёрткой называется мера[]
где обозначает произведение мер и .
Свойства
- Пусть абсолютно непрерывны относительно меры Лебега . Обозначим их производные Радона — Никодима:
Тогда также абсолютно непрерывна относительно , и её производная Радона — Никодима имеет вид[]
- Если — вероятностные меры, то также является вероятностной мерой.
Свёртка распределений
Если — распределения двух независимых случайных величин и , то[]
где — распределение суммы . В частности, если абсолютно непрерывны и имеют плотности , то случайная величина также абсолютно непрерывна и её плотность имеет вид:
См. также
- Обратная свертка (деконволюция)
- Взаимнокорреляционная функция
- Автокорреляционная функция
- Свёртка последовательностей
Примечания
- ↑ Domínguez A. A History of the Convolution Operation // IEEE Pulse. — 2015. — Vol. 6, no. 1. — P. 38—49. Архивировано 3 февраля 2016 года.
- ↑ Slyusar, V. I. (December 27, 1996). "End products in matrices in radar applications" (PDF). Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50—53. Архивировано (PDF) 27 июля 2020. Дата обращения: 1 августа 2020.
- ↑ Slyusar, V. I. (1997-05-20). "Analytical model of the digital antenna array on a basis of face-splitting matrix products" (PDF). Proc. ICATT-97, Kyiv: 108—109. Архивировано (PDF) 25 января 2020. Дата обращения: 1 августа 2020.
- ↑ Slyusar, V. I. (1997-09-15). "New operations of matrices product for applications of radars" (PDF). Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73—74. Архивировано (PDF) 25 января 2020. Дата обращения: 1 августа 2020.
- ↑ Slyusar, V. I. (March 13, 1998). "A Family of Face Products of Matrices and its Properties" (PDF). Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz.- 1999. 35 (3): 379—384. doi:10.1007/BF02733426. Архивировано (PDF) 25 января 2020. Дата обращения: 1 августа 2020.
- ↑ Slyusar, V. I. (2003). "Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels" (PDF). Radioelectronics and Communications Systems. 46 (10): 9—17. Архивировано (PDF) 20 сентября 2020. Дата обращения: 1 августа 2020.
- ↑ Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps. SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
Литература
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, — М.: Наука, 2004 (7-е изд.).
- Ширяев А. Н. Вероятность, — М.: Наука. 1989.
- Напалков В. В. Уравнения свертки в многомерных пространствах. — М., Наука, 1982. — Тираж 3500 экз. — 240 с.
Ссылки
- Java-Applet
- Java-Applet
- Линейная и циклическая свертка. Дата обращения: 15 ноября 2010.


























![{\displaystyle {\mathfrak {F}}[f*g]={\mathfrak {F}}[f]\cdot {\mathfrak {F}}[g]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b49a75e4903ad893bf282b14d5f47d7d9fcdb4)
![{\displaystyle {\mathfrak {F}}[]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc7fb12e05f425948c9b1873c57f8785ac4058f)






























































