
Специа́льная тео́рия относи́тельности — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Фактически СТО описывает геометрию четырёхмерного пространства-времени и основана на плоском пространстве Минковского. Обобщение СТО для сильных гравитационных полей называется общей теорией относительности.

Сингони́я — классификация кристаллографических групп симметрии, кристаллов и кристаллических решёток в зависимости от системы координат ; группы симметрии с единой координатной системой объединяются в одну сингонию. Кристаллы, принадлежащие к одной и той же сингонии, имеют подобные углы и рёбра элементарных ячеек.

Теоре́ма Мёнье́ — даёт выражение для кривизны кривой, лежащей на поверхности.
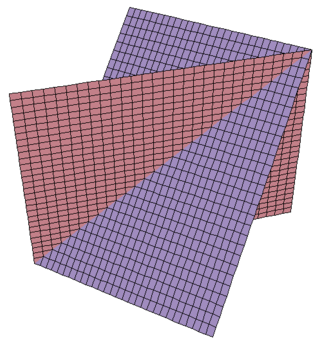
Пло́скость — одно из фундаментальных понятий в геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. В тесной связи с плоскостью принято рассматривать принадлежащие ей точки и прямые; они также, как правило, вводятся как неопределяемые понятия, свойства которых задаются аксиоматически.

Неравенство Птолемея — неравенство на 6 расстояний между четвёркой точек на плоскости.
Эллипти́ческий интегра́л — некоторая функция  над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
 ,
,

Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью.
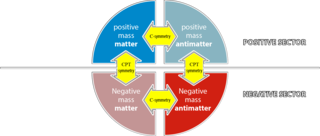
Биметрические теория гравитации — альтернативные теории гравитации, в которых вместо одного метрического тензора используются два или более. Часто вторая метрика вводится только при высоких энергиях, в предположении, что скорость света может зависеть от энергии. Наиболее известными примерами биметрических теорий являются теория Розена и релятивистская теория гравитации.

Моде́ль Ло́тки — Вольте́рры — модель взаимодействия двух видов типа «хищник — жертва», названная в честь её авторов, которые предложили модельные уравнения независимо друг от друга.
Через каждую точку однополостного гиперболоида проходят две различные прямые, целиком расположенные на этой поверхности.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, достаточная для полного описания гравитационного поля в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой  . Гравитационный потенциал в данной точке пространства, задаваемой радиус-вектором
. Гравитационный потенциал в данной точке пространства, задаваемой радиус-вектором  , численно равен работе, которую выполняют гравитационные силы при перемещении пробного тела единичной массы по произвольной траектории из данной точки в точку, где потенциал принят равным нулю. Гравитационный потенциал равен отношению потенциальной энергии
, численно равен работе, которую выполняют гравитационные силы при перемещении пробного тела единичной массы по произвольной траектории из данной точки в точку, где потенциал принят равным нулю. Гравитационный потенциал равен отношению потенциальной энергии  небольшого тела, помещённого в эту точку, к массе тела
небольшого тела, помещённого в эту точку, к массе тела  . Как и потенциальная энергия, гравитационный потенциал всегда определяется с точностью до постоянного слагаемого, обычно (но не обязательно) подбираемого таким образом, чтобы потенциал на бесконечности оказался нулевым. Например, гравитационный потенциал на поверхности Земли, отсчитываемый от бесконечно удалённой точки (если пренебречь гравитацией Солнца, Галактики и других тел), отрицателен и равен −62,7·106 м2/с2 (половине квадрата второй космической скорости).
. Как и потенциальная энергия, гравитационный потенциал всегда определяется с точностью до постоянного слагаемого, обычно (но не обязательно) подбираемого таким образом, чтобы потенциал на бесконечности оказался нулевым. Например, гравитационный потенциал на поверхности Земли, отсчитываемый от бесконечно удалённой точки (если пренебречь гравитацией Солнца, Галактики и других тел), отрицателен и равен −62,7·106 м2/с2 (половине квадрата второй космической скорости).
Теория Эйнштейна — Картана (ЭК) была разработана как расширение общей теории относительности, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина материальных полей. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен общей теории относительности, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к общей теории относительности в условиях современной Вселенной настолько малы, что пока не видно даже гипотетических путей для их измерения.
Уравнение ренормгруппы — дифференциальное уравнение для корреляционных функций (пропагаторов), показывающее их независимость от масштаба рассмотрения. Оно имеет место, например, при рассмотрении динамики системы вблизи критической точки.

Теорема Кейси или Кэзи — теорема в евклидовой геометрии, обобщающая неравенство Птолемея. Названа по имени ирландского математика Джона Кейси.

Бидуга́ — гладкая плоская кривая, составленная из двух круговых дуг, меньших полной окружности. Одной из дуг может быть отрезок прямой. Бидуги были предложены для геометрического моделирования кривых с заданными граничными точками и касательными в них. В классе бидуг эта задача имеет целое семейство решений, и требует дополнительных условий для нахождения конкретных кривых. Таковыми могут быть задание кривизны или поворота одной из дуг, фиксированная длина кривой, требование минимизации скачка кривизны в точке сопряжения, и т. п.

Теорема Фогта устанавливает соотношения между граничными углами плоской кривой с монотонно изменяющейся кривизной (спиральной дуги) в зависимости от возрастания / убывания кривизны.
Тождества Фирца — тождества линейной алгебры, связывающие различные выражения в виде произведений матриц Паули, матриц Гелл-Манна и матриц Дирака, различающиеся между собой перестановкой индексов. Используются в теоретической физике.

Су́ффиксный автома́т — структура данных, позволяющая хранить в сжатом виде и обрабатывать информацию, связанную с подстроками данной строки. Представляет собой детерминированный конечный автомат, принимающий все суффиксы слова  и только их, и обладающий наименьшим возможным числом состояний среди всех таких автоматов. Менее формально, суффиксный автомат — это ориентированный ациклический граф с выделенной начальной вершиной и набором «финальных» вершин, дуги которого помечены символами, такой что у любой вершины символы на исходящих из неё дугах попарно различны и для любого суффикса слова
и только их, и обладающий наименьшим возможным числом состояний среди всех таких автоматов. Менее формально, суффиксный автомат — это ориентированный ациклический граф с выделенной начальной вершиной и набором «финальных» вершин, дуги которого помечены символами, такой что у любой вершины символы на исходящих из неё дугах попарно различны и для любого суффикса слова  существует путь из начальной вершины в некоторую финальную вершину, символы на котором при конкатенации образуют данный суффикс. Из всех графов, удовлетворяющих данному описанию, суффиксным автоматом называется тот, который обладает наименьшим возможным числом вершин.
существует путь из начальной вершины в некоторую финальную вершину, символы на котором при конкатенации образуют данный суффикс. Из всех графов, удовлетворяющих данному описанию, суффиксным автоматом называется тот, который обладает наименьшим возможным числом вершин.






































