
Те́нзор — применяемый в математике и физике математический объект линейной алгебры, заданный на векторном пространстве конечной размерности. В физике в качестве векторного пространства обычно выступает физическое трёхмерное пространство или четырёхмерное пространство-время, а компонентами тензора являются координаты (проекции) взаимосвязанных физических величин. Использование тензоров в физике позволяет глубже понять физические законы и уравнения, упростить их запись за счёт сведения многих связанных физических величин в один тензор, а также записывать уравнения в форме, не зависящей от выбранной системы отсчёта.

Корреля́ция, или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин, при этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.
Свёртка в тензорном исчислении — операция понижения валентности тензора на 2, переводящая тензор валентности  в тензор валентности
в тензор валентности  .
.
Ковариантная производная — обобщение понятия производной для тензорных полей на многообразиях. Понятие ковариантной производной тесно связано с понятием аффинной связности.
Метри́ческий те́нзор, или ме́трика, — симметричное тензорное поле ранга (0,2) на гладком многообразии, посредством которого задаётся скалярное произведение векторов в касательном пространстве. Иначе говоря, метрический тензор задаёт билинейную форму на касательном пространстве к этой точке, обладающую свойствами скалярного произведения и гладко зависящую от точки.

Многоме́рное норма́льное распределе́ние в теории вероятностей — это обобщение одномерного нормального распределения. Случайный вектор, имеющий многомерное нормальное распределение, называется гауссовским вектором.
Символ Ле́ви-Чиви́ты — математический символ, который используется в тензорном анализе. Назван в честь итальянского математика Туллио Леви-Чивиты. Обозначается  . Здесь приведён символ для трёхмерного пространства, для других размерностей меняется количество индексов.
. Здесь приведён символ для трёхмерного пространства, для других размерностей меняется количество индексов.

В механике сплошной среды механическое напряжение — это физическая величина, которая выражает внутренние силы, которые соседние частицы в непрерывной среде оказывают друг на друга, а деформация — это мера изменения геометрических размеров среды. Например, когда сплошная вертикальная штанга поддерживает груз, каждая частица в штанге давит на частицы, находящиеся непосредственно под ней. Когда жидкость находится в закрытом контейнере под давлением, каждая частица сталкивается со всеми окружающими частицами. Стенки контейнера и поверхность, создающая давление, прижимаются к ним в соответствии с силой реакции. Эти макроскопические силы на самом деле являются чистым результатом очень большого количества межмолекулярных сил и столкновений между частицами в этих средах. Механическое напряжение или в дальнейшем напряжение часто обозначается строчной греческой буквой сигма σ.
Метод главных компонент — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретён Карлом Пирсоном в 1901 году. Применяется во многих областях, в том числе в эконометрике, биоинформатике, обработке изображений, для сжатия данных, в общественных науках.
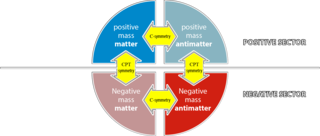
Биметрические теория гравитации — альтернативные теории гравитации, в которых вместо одного метрического тензора используются два или более. Часто вторая метрика вводится только при высоких энергиях, в предположении, что скорость света может зависеть от энергии. Наиболее известными примерами биметрических теорий являются теория Розена и релятивистская теория гравитации.
Звезда́ Хо́джа — важный линейный оператор из пространства q-векторов в пространство (n − q)-форм. Метрический тензор задаёт канонический изоморфизм между пространствами q-форм и q-векторов, поэтому обычно звездой Ходжа называют оператор из пространства дифференциальных форм размерности q в пространство форм размерности n − q.

4-тензоры, четырёхте́нзоры — класс математических объектов, используемый для описания некоторых физических полей в релятивистской физике, тензор, определённый на четырёхмерном пространстве-времени.
- Замечание: в литературе 4-тензоры часто называются просто тензорами, а размерность и природа векторного пространства (многообразия), на котором они заданы в этом случае оговариваются явно или очевидны из контекста.
Ковариа́нтность и контравариа́нтность — используемые в математике и в физике понятия, характеризующие то, как тензоры изменяются при преобразованиях базисов в соответствующих пространствах или многообразиях. Контравариантными называют «обычные» компоненты, которые при смене базиса пространства изменяются с помощью преобразования, обратного преобразованию базиса. Ковариантными — те, которые изменяются так же, как и базис.
В математике и теоретической физике тензор называется симметричным по двум индексам i и j, если он не меняется при перестановке этих индексов:


Гауссова кривизна — мера искривления поверхности в окрестности какой-либо её точки. Гауссова кривизна является объектом внутренней геометрии поверхностей, то есть она не изменяется при изометрических изгибаниях.
Алгебраическое тождество Бьянки — определённый вид симметрии тензора кривизны. Также известно как тождество Бьянки — Падова), или первое тождество Бьянки. Тождество было найдено Грегорио Риччи-Курбастро, но оно называется первым тождеством Бьянки, потому что оно похоже на дифференциальное тождество, описанное Луиджи Бьянки.
Эластичность замещения — применяемый в экономической теории показатель, характеризующий производственную функцию или функцию полезности, и показывающий на сколько процентов необходимо изменить отношение факторов производства при изменении их предельной нормы замещения на 1 %, чтобы объём выпуска оставался неизменным.


![{\displaystyle \scriptstyle T_{[ij]}={1 \over 2}\left(T_{ij}-T_{ji}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29dd00af72830bf8d2dd8c196a3e8b48669a46fe)



![{\displaystyle A_{[m_{1}\ldots m_{k}]m_{k+1}m_{q}}^{n_{1}\ldots n_{p}}={\frac {1}{k!}}\sum _{\sigma (m_{1}\ldots m_{k})}\operatorname {sgn} \sigma \cdot A_{\sigma (m_{1})\ldots \sigma (m_{k})m_{k+1}m_{q}}^{n_{1}\ldots n_{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3a7f839d446dca011681170c873cccc38ec02)

![{\displaystyle A_{[klm]}={\frac {1}{3!}}(A_{klm}+A_{lmk}+A_{mkl}-A_{kml}-A_{lkm}-A_{mlk})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/445115880dd469a57a3c54a5350a72914cd92d27)
![{\displaystyle A_{k}^{q[l}B_{pr}^{m]}={\frac {1}{2!}}(A_{k}^{ql}B_{pr}^{m}-A_{k}^{qm}B_{pr}^{l})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ff4f4f9ecad590821bec9cc59b578de6792450c)







![{\displaystyle T_{[ij]}\in V\wedge V.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c09407e682021ea86ba2a19d9b8b6e91324019c)



















