Окта́эдр — многогранник с восемью гранями.
Квадра́тный парке́т, квадратный паркетаж, квадратная мозаика или квадратная решётка — это замощение плоскости равными квадратами, расположенными сторона к стороне, при этом вершины четырёх смежных квадратов находятся в одной точке. Символ Шлефли мозаики — {4,4}, означающий, что вокруг каждой вершины имеется 4 квадрата.
Треуго́льный парке́т или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
Шестиуго́льный парке́т или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Усечение — операция в пространстве любой размерности, которая отсекает вершины многогранника и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.
Линк вершины многогранника или вершинная фигура — многогранник на единицу меньшей размерности, который получается в сечении исходного многогранника плоскостью, срезающей одну вершину. В частности линк вершины содержит информацию о порядке следования граней многогранника вокруг одной вершины.
Соты — это заполнение пространства непересекающимися многогранниками, при котором не остаётся незаполненного пространства. Это обобщение математического понятия мозаика или паркет на любую размерность.
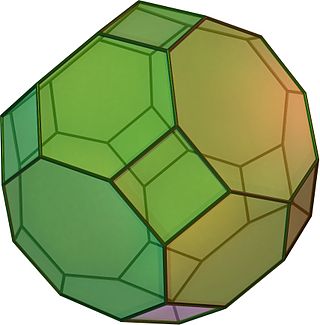
Усечённый кубооктаэдр, усечённый кубоктаэдр — полуправильный многогранник с 12 квадратными гранями, 8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника, 48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию, усечённый кубооктаэдр является зоноэдром.
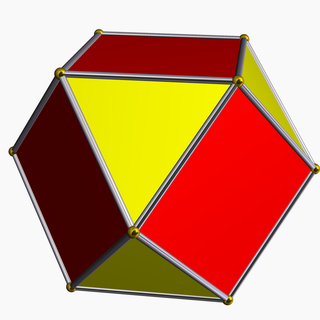
В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек. Получающийся многогранник будет ограничен фасетами вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Так, например, r{4,3} — спрямлённый куб, т.е. кубооктаэдр.
Квазипра́вильный многогра́нник — полуправильный многогранник, который имеет в точности два вида правильных граней, поочерёдно следующих вокруг каждой вершины. Эти многогранники рёберно транзитивны, а потому на шаг ближе к правильным многогранникам, чем полуправильные, которые лишь вершинно транзитивны.
Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.
В пятимерной геометрии пятимерный многогранник или 5-многогранник — это многогранник в пространстве размерности 5, ограниченный 4-мерными гранями. При этом каждая 3-мерная многогранная ячейка принадлежит ровно двум 4-мерным граням.
Четырёхмерный многогранник — многогранник в четырёхмерном пространстве. Многогранник является связанной замкнутой фигурой, состоящей из многогранных элементов меньшей размерности — вершин, рёбер, граней (многоугольников) и ячеек. Каждая грань принадлежит ровно двум ячейкам.
Однородная мозаика — вершинно транзитивная мозаика на плоскости с правильными многоугольными гранями.
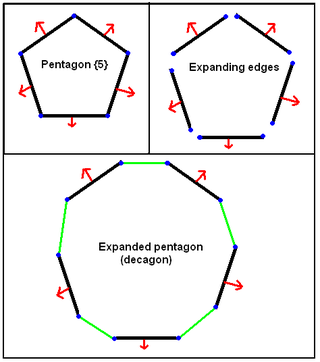
Растяжение — операция над многогранником, при которой фасеты отделяются и передвигаются радиально в направлении от центра, новые фасеты образуются на разделённых элементах. Эти же операции можно понимать как операции, сохраняющие фасеты на месте, но уменьшающие их в размерах.
В гиперболическом трёхмерном пространстве додекаэдральные соты порядка 4 — это одна из четырёх компактных правильных заполняющих пространство мозаик. Имея символ Шлефли {5,3,4}, соты имеют четыре додекаэдра вокруг каждого ребра и 8 додекаэдров вокруг каждой вершины в октаэдральном расположении. Вершины сот строятся на 3 ортогональных осях. Двойственным телом сот являются кубические соты порядка 5.
Нотация Конвея для многогранников, разработанная Конвеем и продвигаемая Хартом, используется для описания многогранников, опираясь на затравочный многогранник, модифицируемый различными префикс-операциями.
Операция snub или отсечение вершин — это операция, применяемая к многогранникам. Термин появился из названий, данных Кеплером двум архимедовым телам — плосконосый куб и плосконосый додекаэдр. В общем случае плосконосые формы имеют хиральную симметрию двух видов, с ориентацией по часовой стрелке и против часовой стрелки. Согласно названиям Кеплера, отсечение вершин можно рассматривать как растяжение правильного многогранника, когда исходные грани отодвигаются от центра и поворачиваются относительно центров, вместо исходных вершин добавляются многоугольники с центрами в этих вершинах, а пары треугольников заполняют пространство между исходными рёбрами.
В гиперболическом пространстве размерности 3 восьмиугольные соты порядка 4 — правильные паракомпактные соты. Они называются паракомпактными, поскольку имеют бесконечные вершинные фигуры со всеми вершинами как идеальные точки на бесконечности. Если многогранник задан символом Шлефли {3,4,4}, он имеет четыре октаэдра {3,4} вокруг каждого ребра и бесконечное число октаэдров вокруг каждой вершины в квадратном паркете {4,4}, в качестве расположения вершин.
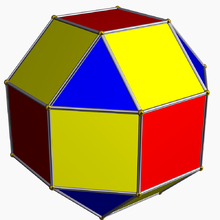
Для многогранников больших размерностей скашивание даёт последовательность из правильного многогранника до его полного усечения. Кубооктаэдр можно рассматривать как полное усечение, например, тетраэдра. 
