Скорость звука
| 0 °C, 101325 Па | м/с | км/ч |
|---|---|---|
| Азот | 333 | 1202,4 |
| Аммиак | 415 | 1494,0 |
| Ацетилен | 327 | 1177,2 |
| Водород | 1284 | 4622,4 |
| Воздух | 331 | 1191,6 |
| Гелий | 965 | 3474,0 |
| Кислород | 316 | 1137,6 |
| Метан | 430 | 1548,0 |
| Угарный газ | 338 | 1216,8 |
| Неон | 435 | 1566,0 |
| Углекислый газ | 259 | 932,4 |
| Хлор | 206 | 741,6 |
| Жидкости | ||
| Вода | 1403 | 5050,8 |
| Ртуть | 1383 | 4978,0 |
| Твёрдые тела | ||
| Бериллий | 12600 | 45360,0 |
| Алмаз | 12000 | 43200,0 |
| Железо | 5950 | 21420,0 |
| Золото | 3240 | 11664,0 |
| Литий | 6000 | 21600,0 |
| Стекло | 4800 | 17280,0 |
Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).
Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.
Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.
История измерения скорости звука
Уже у античных авторов встречается указание на то, что звук обусловлен колебательным движением тела (Птолемей, Евклид). Аристотель отмечает, что скорость звука имеет конечную величину, и правильно представляет себе природу звука[2]. Попытки экспериментального определения скорости звука относятся к первой половине XVII в. Ф. Бэкон в «Новом органоне» указал на возможность определения скорости звука путём сравнения промежутков времени между вспышкой света и звуком выстрела. Применив этот метод, различные исследователи (М. Мерсенн, П. Гассенди, У. Дерхам, группа учёных Парижской академии наук — Д. Кассини, Ж. Пикар, Гюйгенс, Рёмер) определили значение скорости звука (в зависимости от условий экспериментов, 350—390 м/с).
Теоретически вопрос о скорости звука впервые рассмотрел И. Ньютон в своих «Началах»; он фактически предполагал изотермичность распространения звука, поэтому получил заниженную оценку. Правильное теоретическое значение скорости звука было получено Лапласом[3][4][5][6].
В 2020 году физики рассчитали максимально возможную скорость звука, которая составляет 36 км/с (этот показатель приблизительно втрое превышает скорость звука в алмазе (12 км/с), самом твёрдом известном материале в мире). Теория предсказывает наибольшую скорость звука в среде твёрдого атомарного металлического водорода, при давлении выше 1 млн атмосфер[7][8].
Расчёт скорости звука в жидкости и газе

Скорость звука в однородной жидкости (или газе) вычисляется по формуле:
В частных производных:
- где — адиабатическая сжимаемость среды;
- — плотность;
- — изобарная теплоёмкость;
- — изохорная теплоёмкость;
- , , — давление, удельный объём и температура;
- — энтропия среды.
Для идеальных газов эта формула выглядит так:
- ,
- где — показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных;
- — постоянная Больцмана;
- — универсальная газовая постоянная;
- — абсолютная температура;
- — молекулярная масса;
- — молярная масса;
- ;
- — средняя скорость теплового движения частиц газа.
По величине скорость звука в газах близка к средней скорости теплового движения молекул (см. Распределение Максвелла) и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры.
Данные выражения являются приближёнными, поскольку основываются на уравнениях, описывающих поведение идеального газа. При больших давлениях и температурах необходимо вносить соответствующие поправки.
Для расчёта сжимаемости многокомпонентной смеси, состоящей из невзаимодействующих друг с другом жидкостей и/или газов, применяется уравнение Вуда. Это же уравнение применимо и для оценки скорости звука в нейтральных взвесях.
Для растворов и других сложных физико-химических систем (например, природный газ, нефть) эти упрощённые выражения могут давать очень большую погрешность.
Влияние высоты на атмосферную акустику

В атмосфере Земли температура является главным фактором, влияющим на скорость звука. Для данного идеального газа с постоянной теплоемкостью и составом скорость звука зависит исключительно от температуры. В таком идеальном случае эффекты понижения плотности и понижения давления на высоте компенсируют друг друга, и на скорость звука влияет только температура.
Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до 11 км, звук преломляется вверх, удаляясь от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника[9]. Уменьшение скорости звука с высотой называется отрицательным градиентом скорости звука.
Однако выше 11 км в этой тенденции происходят изменения. В частности, в стратосфере на высоте более 20 км скорость звука увеличивается с высотой из-за повышения температуры в результате нагрева озонового слоя. Это дает положительный знак градиента скорости звука в этой области. Ещё одна область положительного градиента наблюдается на очень больших высотах, в слое называемом термосферой (лежащем выше 90 км).
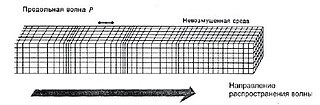
Твёрдые тела
Смотрите также: P-волна
Смотрите также: S-волна
В однородных твёрдых телах могут существовать два типа объёмных волн, отличающихся друг от друга поляризацией колебаний относительно направления распространения волны: продольная (P-волна) и поперечная (S-волна). Скорость распространения первой всегда выше, чем скорость второй :
где — модуль всестороннего сжатия, — модуль сдвига, — модуль Юнга, — коэффициент Пуассона. Как и для случая с жидкой или газообразной средой, при расчётах должны использоваться адиабатические модули упругости.
В многофазных средах из-за явлений неупругого поглощения энергии скорость звука, вообще говоря, зависит от частоты колебаний (то есть наблюдается дисперсия скорости). Например, оценка скорости упругих волн в двухфазной пористой среде может быть выполнена с применением уравнений теории Био-Николаевского. При достаточно высоких частотах (выше частоты Био) в такой среде возникают не только продольные и поперечные волны, но также и продольная волна II-рода. При частоте колебаний ниже частоты Био, скорость упругих волн может быть приблизительно оценена с использованием гораздо более простых уравнений Гассмана.
При наличии границ раздела, упругая энергия может передаваться посредством поверхностных волн различных типов, скорость которых отличается от скорости продольных и поперечных волн. Энергия этих колебаний может во много раз превосходить энергию объёмных волн.
Скорость звука в воде


В чистой воде скорость звука составляет около 1500 м/с (см. опыт Колладона — Штурма) и увеличивается с ростом температуры.
Важное прикладное значение имеет также скорость звука в солёной воде океанов. Скорость звука увеличивается с увеличением солёности и температуры. При увеличении давления скорость также возрастает, то есть, увеличивается с глубиной. Предложено несколько различных эмпирических формул для вычисления скорости распространения звука в воде в зависимости от температуры, солёности и давления (глубины).
Например, формула Вильсона 1960 года для нулевой глубины даёт следующее значение скорости звука:
- где — скорость звука в метрах в секунду,
- — температура в градусах Цельсия,
- — солёность в промилле.
Иногда также пользуются упрощённой формулой Лероя:
- где — глубина в метрах.
Эта формула обеспечивает точность около 0,1 м/с для °C и при м.
При температуре +24 °C, солёности 35 промилле и нулевой глубине скорость звука равна около 1532,3 м/c. При °C, глубине 100 м и той же солёности скорость звука равна 1468,5 м/с[10].
| Коэффициент | Значение | Коэффициент | Значение |
|---|---|---|---|
| 1402,388 | 7,166·10−5 | ||
| 5,03830 | 2,008·10−6 | ||
| -5,81090·10−2 | -3,21·10−8 | ||
| 3,3432·10−4 | 9,4742·10−5 | ||
| -1,47797·10−6 | -1,2583·10−5 | ||
| 3,1419·10−9 | -6,4928·10−8 | ||
| 0,153563 | 1,0515·10−8 | ||
| 6,8999·10−4 | -2,0142·10−10 | ||
| -8,1829·10−6 | -3,9064·10−7 | ||
| 1,3632·10−7 | 9,1061·10−9 | ||
| -6,1260·10−10 | -1,6009·10−10 | ||
| 3,1260·10−5 | 7,994·10−12 | ||
| -1,7111·10−6 | 1,100·10−10 | ||
| 2,5986·10−8 | 6,651·10−12 | ||
| -2,5353·10−10 | -3,391·10−13 | ||
| 1,0415·10−12 | -1,922·10−2 | ||
| -9,7729·10−9 | -4,42·10−5 | ||
| 3,8513·10−10 | 7,3637·10−5 | ||
| -2,3654·10−12 | 1,7950·10−7 | ||
| 1,389 | 1,727·10−3 | ||
| -1,262·10−2 | -7,9836·10−6 |
Международная стандартная формула, применяемая для определения скорости звука в морской воде известна как формула ЮНЕСКО и описана в работе[11]. Она более сложная, чем простые формулы, приведённые выше, и вместо глубины в неё входит давление как параметр. Оригинальный алгоритм ЮНЕСКО для расчётов по формуле описан в работе N. P. Fofonoff и R. C. Millard[12].
В 1995 году коэффициенты, применяемые в данной формуле были уточнены[13] после принятия международной температурной шкалы 1990 года. Конечная форма формулы ЮНЕСКО имеет следующий вид, входящие в формулу постоянные коэффициенты согласно[13] приведены в таблице:
- где
- Здесь — температура в градусах Цельсия (в диапазоне от 0 °С до 40 °С),
- — солёность в промилле (в диапазоне от 0 до 40 промилле),
- — давление в барах (в диапазоне от 0 до 1000 бар).
В библиотеке приводится исходный код алгоритма ЮНЕСКО на языке C#.
См. также
- Скорость света
- Эффект Доплера
- Сверхзвуковая скорость
- Сверхзвуковой самолёт
- Звуковой барьер
- Число Маха
- Гиперзвуковая скорость
- Сейсмическая волна
Примечания
- ↑ Скорость звука // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 4. Архивировано 9 марта 2011 года.
- ↑ Тимкин С. История естествознания
- ↑ The Speed of Sound. mathpages.com. Дата обращения: 3 мая 2015. Архивировано 25 июля 2020 года.
- ↑ Bannon, Mike; Kaputa, Frank The Newton–Laplace Equation and Speed of Sound. Thermal Jackets. Дата обращения: 3 мая 2015. Архивировано 15 августа 2020 года.
- ↑ Murdin, Paul. Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth (англ.). — Springer Science & Business Media, 2008. — P. 35—36. — ISBN 9780387755342.
- ↑ Fox, Tony. Essex Journal (неопр.). — Essex Arch & Hist Soc, 2003. — С. 12—16.
- ↑ Скорость звука: каков ее предел? / Блог компании ua-hosting.company / Хабр. Дата обращения: 26 декабря 2020. Архивировано 3 декабря 2020 года.
- ↑ Источник. Дата обращения: 26 декабря 2020. Архивировано 30 декабря 2020 года.
- ↑ Everest, F. The Master Handbook of Acoustics. — New York : McGraw-Hill, 2001. — P. 262–263. — ISBN 978-0-07-136097-5.
- ↑ Роберт Дж. Урик (Rodert J. Urick) Основы гидроакустики (Principles of underwater sound) Л: Судостроение, 1978; McGraw-Hill 1975.
- ↑ Chen‐Tung Chen, Frank J. Millero. Speed of sound in seawater at high pressures (англ.) // Journal of the Acoustical Society of America[англ.]. — 1977-11-01. — Vol. 62, iss. 5. — P. 1129—1135. — ISSN 0001-4966. — doi:10.1121/1.381646. Архивировано 5 августа 2019 года.
- ↑ Millard R. C., Jr; Fofonoff N. P. Algorithms for the computation of fundamental properties of seawater (англ.). — 1983. Архивировано 5 августа 2019 года.
- ↑ 1 2 George S. K. Wong, Shi‐ming Zhu. Speed of sound in seawater as a function of salinity, temperature, and pressure (англ.) // Journal of the Acoustical Society of America[англ.]. — 1995-03-01. — Vol. 97, iss. 3. — P. 1732—1736. — ISSN 0001-4966. — doi:10.1121/1.413048. Архивировано 5 августа 2019 года.
Литература
- Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1953;
- Михайлов И. Г., Соловьев В. А., Сырников Ю. П., Основы молекулярной акустики, М., 1964;
- Колесников А. Е., Ультразвуковые измерения, М., 1970;
- Исакович М. А., Общая акустика, М., 1973.