Скрученно удлинённый трёхскатный купол

Скрученно удлинённый трёхскатный купол
(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклый
Комбинаторика
Элементы	20 граней 33 ребра 15 вершин Χ = 2
Грани	16 треугольников 3 квадрата 1 шестиугольник
Конфигурация вершины	3(3.4.3.4) 2x3(33.6) 6(34.4)
Развёртка
Классификация
Обозначения	J22, М4+А6
Группа симметрии	C3v

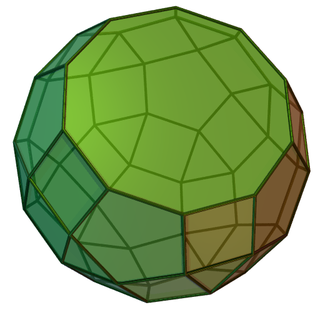
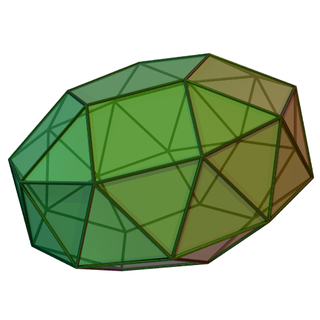
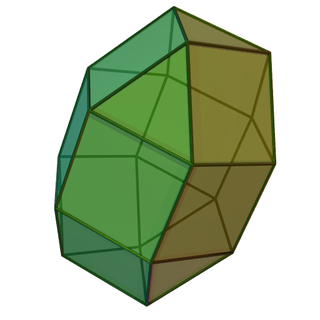
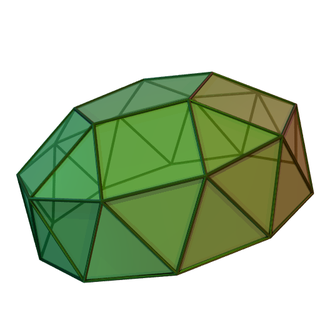
Скру́ченно удлинённый трёхска́тный ку́пол^[1] — один из многогранников Джонсона (J₂₂, по Залгаллеру — М₄+А₆).

Составлен из 20 граней: 16 правильных треугольников, 3 квадратов и 1 правильного шестиугольника. Шестиугольная грань окружена шестью треугольными; каждая квадратная грань окружена четырьмя треугольными; среди треугольных граней 6 окружены шестиугольной и двумя треугольными, 1 — тремя квадратными, 3 — двумя квадратными и треугольной, 3 — квадратной и двумя треугольными, остальные 3 — тремя треугольными.

Имеет 33 ребра одинаковой длины. 6 рёбер располагаются между шестиугольной и треугольной гранями, 12 рёбер — между квадратной и треугольной, остальные 15 — между двумя треугольными.

У скрученно удлинённого трёхскатного купола 15 вершин. В 6 вершинах сходятся шестиугольная и три треугольных грани; в 3 вершинах — две квадратных и две треугольных; в остальных 6 — квадратная и четыре треугольных.

Скрученно удлинённый трёхскатный купол можно получить из двух многогранников — трёхскатного купола (J₃) и правильной шестиугольной антипризмы, все рёбра у которой равны, — приложив их друг к другу шестиугольными гранями.

Если скрученно удлинённый трёхскатный купол имеет ребро длины ${\displaystyle a}$, его площадь поверхности и объём выражаются как

${\displaystyle S=\left(3+{\frac {11{\sqrt {3}}}{2}}\right)a^{2}\approx 12{,}5262794a^{2},}$

${\displaystyle V={\sqrt {2}}\left({\frac {5}{6}}+{\sqrt {1+{\sqrt {3}}}}\right)a^{3}\approx 3{,}5160531a^{3}.}$

• Weisstein, Eric W. Скрученно удлинённый трёхскатный купол (англ.) на сайте Wolfram MathWorld.