Лине́йное отображе́ние — обобщение линейной числовой функции на случай более общего множества аргументов и значений. Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.
Риманово многообразие, или риманово пространство (M, g), — это (вещественное) гладкое многообразие M, в котором каждое касательное пространство снабжено скалярным произведением g — метрическим тензором, меняющимся от точки к точке гладким образом. Другими словами, риманово многообразие — это дифференцируемое многообразие, в котором касательное пространство в каждой точке является конечномерным евклидовым пространством.
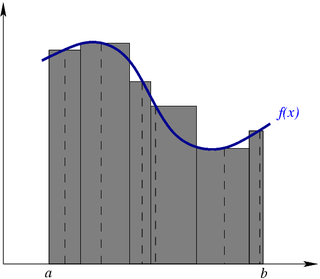
Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.
Моме́нт си́лы — векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. Определяется как векторное произведение радиус-вектора точки приложения силы  и вектора силы
и вектора силы  . Моменты сил, образующиеся в разных условиях, в технике могут иметь названия: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент, скру́чивающий момент.
. Моменты сил, образующиеся в разных условиях, в технике могут иметь названия: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент, скру́чивающий момент.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.
Краевая задача — задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Краевые задачи для гиперболических и параболических уравнений часто называют начально-краевыми или смешанными, потому что в них задаются не только граничные, но и начальные условия.
Опера́тор — математическое отображение между множествами, в котором каждое из них наделено какой-либо дополнительной структурой. Понятие оператора используется в различных разделах математики для отличия от другого рода отображений ; точное значение зависит от контекста, например в функциональном анализе под операторами понимают отображения, ставящие в соответствие функции другую функцию.

Фу́нкция Гри́на — функция, используемая для решения линейных неоднородных дифференциальных уравнений с граничными условиями . Названа в честь английского математика Джорджа Грина, который первым развил соответствующую теорию в 1830-е годы.
Обобщённая фу́нкция, или распределе́ние, — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.
Абсолютная непрерывность — свойство функций и мер, состоящее, неформально говоря, в выполнении теоремы Ньютона — Лейбница о связи между интегрированием и дифференцированием. Обычно эта теорема формулируется в терминах интеграла Римана и включает в свои условия интегрируемость производной по Риману. При переходе к более общему интегралу Лебега естественное требование существования измеримой производной почти всюду становится слишком слабым, и для выполнения соотношения, аналогичного теореме Ньютона — Лейбница, необходимо более тонкое условие, которое и называется абсолютной непрерывностью. Это понятие переносится на меры с помощью производной Радона — Никодима.

Формула Ньютона — Лейбница, или основная формула анализа, или формула Барроу даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Точное нахождение первообразной произвольных функций — процедура более сложная, чем «дифференцирование», то есть нахождение производной. Зачастую, выразить интеграл в элементарных функциях невозможно.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, достаточная для полного описания гравитационного поля в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой  . Гравитационный потенциал в данной точке пространства, задаваемой радиус-вектором
. Гравитационный потенциал в данной точке пространства, задаваемой радиус-вектором  , численно равен работе, которую выполняют гравитационные силы при перемещении пробного тела единичной массы по произвольной траектории из данной точки в точку, где потенциал принят равным нулю. Гравитационный потенциал равен отношению потенциальной энергии
, численно равен работе, которую выполняют гравитационные силы при перемещении пробного тела единичной массы по произвольной траектории из данной точки в точку, где потенциал принят равным нулю. Гравитационный потенциал равен отношению потенциальной энергии  небольшого тела, помещённого в эту точку, к массе тела
небольшого тела, помещённого в эту точку, к массе тела  . Как и потенциальная энергия, гравитационный потенциал всегда определяется с точностью до постоянного слагаемого, обычно (но не обязательно) подбираемого таким образом, чтобы потенциал на бесконечности оказался нулевым. Например, гравитационный потенциал на поверхности Земли, отсчитываемый от бесконечно удалённой точки (если пренебречь гравитацией Солнца, Галактики и других тел), отрицателен и равен −62,7·106 м2/с2 (половине квадрата второй космической скорости).
. Как и потенциальная энергия, гравитационный потенциал всегда определяется с точностью до постоянного слагаемого, обычно (но не обязательно) подбираемого таким образом, чтобы потенциал на бесконечности оказался нулевым. Например, гравитационный потенциал на поверхности Земли, отсчитываемый от бесконечно удалённой точки (если пренебречь гравитацией Солнца, Галактики и других тел), отрицателен и равен −62,7·106 м2/с2 (половине квадрата второй космической скорости).
Спектральная мера - это отображение, определённое на  -алгебре подмножеств заданного множества, значения которого являются ортогональными проекторами в гильбертовом пространстве.
-алгебре подмножеств заданного множества, значения которого являются ортогональными проекторами в гильбертовом пространстве.
Эволюцио́нный проце́сс ― процесс, обладающий свойством детерминированности, конечномерности и дифференцируемости.


![{\displaystyle L^{1}([a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cf02a5838299a9ec9af75e35122831d9c15e173)













![{\displaystyle v\colon [-1,1]\to [-1,1]\colon t\mapsto v(t)={\begin{cases}1,&t>0;\\0,&t=0;\\-1,&t<0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/580bd52779fd33128314e80407d80ab14d948277)

















