В теории вероятностей случайная мера — это меро-значимый случайный элемент.[1][2] Случайная мера вида
где 
Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой.
Моме́нт и́мпульса — векторная физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение.
Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.
Мера Жордана — один из способов формализации понятия длины, площади и 
Принцип неопределённости Гейзенбе́рга в квантовой механике — фундаментальное соображение, устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами.
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез, основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Лагранжева механика — формулировка классической механики, введённая Луи Лагранжем в 1788 году. В лагранжевой механике траектория объекта получается при помощи отыскания пути, который минимизирует действие — интеграл от функции Лагранжа по времени. Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией.
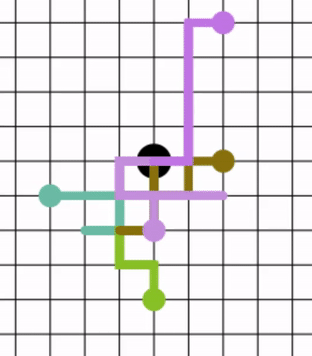
Случайное блуждание — математический объект, известный как стохастический или случайный процесс, который описывает путь, состоящий из последовательности случайных шагов в каком-нибудь математическом пространстве.
Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет система (тело) в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой. Теплота — это одна из основных термодинамических величин в классической феноменологической термодинамике. Количество теплоты входит в стандартные математические формулировки первого и второго начал термодинамики.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Га́мма-распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр 
Сходи́мость по распределе́нию в теории вероятностей — вид сходимости случайных величин.
Бесконе́чно дели́мое распределе́ние в теории вероятностей — распределение случайной величины такой, что она может быть представлена в виде произвольного количества независимых, одинаково распределённых слагаемых.
Гистогра́мма в математической статистике — это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.
Стохастический интеграл — интеграл вида 
Сосиска Винера — это окрестность траектории броуновского движения на момент времени 
Лемма о малом искажении утверждает, что множество из
Псевдослучайная функция Наора — Рейнгольда — псевдослучайная функция, введённая в 1997 году Мони Наором и Омером Рейнгольдом для построения различных криптографических примитивов в симметричном шифровании и криптографии с открытым ключом. Отличительными особенностями данной псевдослучайной функции являются низкая вычислительная сложность и высокая криптографическая стойкость. Данные свойства вместе с тем фактом, что распределение значений данной функции близко к равномерному, позволяют использовать ее в качестве основы для многих криптографических схем.
Оценка Чернова даёт экспоненциально убывающие оценки вероятности больших отклонений сумм независимых случайных величин. Эти оценки являются более точными, чем оценки, полученные с использованием первых или вторых моментов, такие как неравенство Маркова или неравенство Чебышёва, которые дают лишь степенной закон убывания. Вместе с тем оценка Чернова требует, чтобы случайные величины были независимы в совокупности — условие, которое ни неравенство Маркова, ни неравенство Чебышёва не требуют, хотя неравенство Чебышёва требует попарную независимость случайных величин.