
О́бщая тео́рия относи́тельности — общепринятая в настоящее время теория тяготения, описывающая тяготение как проявление геометрии пространства-времени. Предложена Альбертом Эйнштейном 25 ноября 1915 года.
Горизо́нт собы́тий — граница в астрофизике, за которой события не могут повлиять на наблюдателя.
Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом (скаляром) в специальной и общей теории относительности.

Замедление времени — разница в затраченном времени, измеренная двумя часами, либо из-за того, что они имеют разную скорость относительно друг друга, либо из-за разницы в гравитационном потенциале между их местоположениями. После компенсации изменяющихся задержек сигнала из-за изменяющегося расстояния между наблюдателем и движущимися часами наблюдатель будет измерять движущиеся часы как идущие медленнее, чем часы, которые находятся в покое в собственной системе отсчёта наблюдателя. Часы, которые находятся близко к массивному телу, будут показывать меньше прошедшего времени, чем часы, расположенные дальше от указанного массивного тела.
Парадо́кс близнецо́в — мысленный эксперимент, при помощи которого пытаются доказать противоречивость специальной теории относительности. Согласно , с точки зрения «неподвижных» наблюдателей все процессы у двигающихся объектов замедляются. С другой стороны, принцип относительности декларирует равноправие инерциальных систем отсчёта. На основании этого строится рассуждение, приводящее к кажущемуся противоречию. Для наглядности рассматривается история двух братьев-близнецов. Один из них отправляется в космический полёт, второй — остаётся на Земле. После полёта путешественник возвращается на Землю. Чаще всего «парадокс» формулируется следующим образом:
Формулировка I. С точки зрения домоседа часы движущегося путешественника имеют замедленный ход времени, поэтому при возвращении они должны отстать от часов домоседа. С другой стороны, в системе отсчета путешественника двигалась и ускорялась Земля, поэтому отстать должны часы домоседа. На самом деле братья равноправны, следовательно, после возвращения их часы должны показывать одно время.
Простра́нство-вре́мя — физическая модель, дополняющая пространство равноправным временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом. Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.

Простра́нство Минко́вского ― четырёхмерное псевдоевклидово пространство сигнатуры  , предложенное в качестве геометрической интерпретации пространства-времени специальной теории относительности.
, предложенное в качестве геометрической интерпретации пространства-времени специальной теории относительности.

Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистским сокращением длины движущегося тела или масштаба, — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя движущиеся относительно него предметы и пространство имеют меньшую длину в направлении движения, чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.
Мировая линия объекта — это путь объекта в 4-мерном пространстве-времени. Это важное понятие в современной физике, и в особенности в теоретической физике.
Гру́ппа Ло́ренца — группа преобразований Лоренца пространства Минковского, сохраняющих начало координат.
В релятивистской физике координатами Риндлера называется координатная система, представляющая часть плоского пространства-времени, также называемого пространством Минковского. Координаты Риндлера были введены Вольфгангом Риндлером для описания пространства-времени равномерно ускоренного наблюдателя.

Гравитацио́нная сингуля́рность — точка в пространстве-времени, через которую невозможно гладко продолжить входящую в неё геодезическую линию. В таких областях становится неприменимым базовое приближение большинства физических теорий, в которых пространство-время рассматривается как гладкое многообразие без края. Часто в гравитационной сингулярности величины, описывающие гравитационное поле, становятся бесконечными или неопределёнными. К таким величинам относятся, например, скалярная кривизна или плотность энергии в сопутствующей системе отсчёта.
Гравитационное замедление времени — форма замедления времени, фактическая разница прошедшего времени между двумя событиями, измеренная наблюдателями, находящимися на разных расстояниях от гравитирующей массы. Чем ниже гравитационный потенциал, тем медленнее течёт время, ускоряющееся с увеличением гравитационного потенциала. Альберт Эйнштейн первоначально предсказал этот эффект в своей теории относительности, и с тех пор он был подтвержден тестами общей теории относительности.

Относительность одновременности в физике — понятие о том, что отдалённая одновременность — происходят ли два пространственно разделённых события в одно и то же время — не абсолютна, а зависит от системы отсчёта наблюдателя.
4-ускоре́ние в релятивистской кинематике — четырёхвектор, обобщающий классическое ускорение и определяющийся как производная 4-скорости по собственному времени частицы:

Сопутствующее расстояние и собственное расстояние — две тесно связанные меры расстояния, применяемые в физической космологии для определения расстояний между объектами. Собственное расстояние примерно соответствует расстоянию до места, где удалённый объект был бы в определённый момент космологического времени, измеренному с помощью длинного ряда линеек, протянутых от нашей позиции до позиции объекта в это время, и меняющемуся с течением времени в связи с расширением Вселенной. Концепция сопутствующего расстояния «выносит за скобки» расширение Вселенной, позволяя использовать расстояние, которое не изменяется во времени из-за расширения пространства. Сопутствующее расстояние и собственное расстояние определяются таким образом, чтобы они были равны в настоящее время. Таким образом, эти два расстояния, вообще говоря, различны в любой момент времени, отличающийся от момента измерения: расширение Вселенной приводит к изменению собственного расстояния, в то время как сопутствующее расстояние при этом расширении не меняется.
Теория эфира Лоренца (ТЭЛ) уходит своими корнями в «теорию электронов» Х. Лоренца, которая была последней точкой в разработке теорий классического эфира в конце XIX — начале XX века.

Пространственно-временная диаграмма, также известная как Диаграмма Минковского, была разработана в 1908 г. Германом Минковским и дает иллюстрацию свойств пространства и времени в специальной теории относительности. Она позволяет без математических уравнений качественно понимать такие явления, как замедление времени и Лоренцево сокращение.

В теоретической физике диаграмма Пенроуза представляет собой двумерную диаграмму, фиксирующую причинное отношение между различными точками в пространстве-времени. Это расширение диаграммы Минковского, где вертикальное измерение представляет время, горизонтальное — пространство, а наклонные линии под углом 45° соответствуют лучам света. Главное отличие состоит в том, что локально метрика на диаграмме Пенроуза конформно эквивалентна к фактической метрике в пространстве-времени. Конформный фактор выбирается таким образом, что все бесконечное пространство-время преобразуется в диаграмму Пенроуза конечного размера. Для сферически-симметричного пространства-времени каждая точка диаграммы соответствует двумерной сфере.
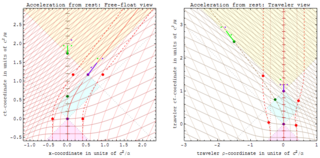
Собственное ускорение в теории относительности — физическое ускорение, испытываемое объектом. Таким образом, это ускорение относительно свободного падения или инерциального наблюдателя, который на мгновение находится в состоянии покоя относительно измеряемого объекта. Гравитация не вызывает собственного ускорения, так как гравитация воздействует на инерциального наблюдателя таким образом, что собственное ускорение не фиксируется. Следствием является то, что все инерционные наблюдатели всегда имеют нулевое собственное ускорение.











