Совместное распределение

Совместное распределе́ние в теории вероятностей — это распределение совместных исходов $(\xi _{1},\xi _{2},\ldots )$ , образованных из нескольких случайных величин $\xi _{1},\xi _{2},\ldots$ . Например, если случайная величина $\xi _{1}$ есть результат кидания первой игральной кости, а случайная величина $\xi _{2}$ есть результат кидания другой игральной кости, то результат $(\xi _{1},\xi _{2})$ совместного кидания игральных костей является составной случайной величиной и имеет совместное распределение.

Определения

Если $\xi _{1},\ldots ,\xi _{n}$ — случайные величины, то каждая составная величина ( $\xi _{1},\ldots ,\xi _{n}$ ) также является случайной величиной. Её распределение называется совместным распределением случайных величин $\xi _{1},\ldots ,\xi _{n}$ .^[1].

Ссылки

↑ Гаральд Крамер, Математические Методы Статистики, перевод с английского А. С. Монина и А. А. Петрова, под редакцией Академика Колмогорова, издание второе, стереотипное, глава 14.2, страница 177.,http://ikfia.ysn.ru/images/doc/Teoriya_veroyatnosti_i_mat_statistika/Kramer1975ru.pdf Архивная копия от 6 февраля 2018 на Wayback Machine

Похожие исследовательские статьи

Случайная величина — переменная, значения которой представляют собой численные исходы некоторого случайного феномена или эксперимента. Другими словами, это численное выражение результата случайного события. Случайная величина является одним из основных понятий теории вероятностей. Для обозначения случайной величины в математике принято использовать греческую букву «кси» $\text{[math]}$ . Если определять случайную величину более строго, то она является функцией $\text{[math]}$ , значения $\text{[math]}$ которой численно выражают исходы $\text{[math]}$ случайного эксперимента. Одним из требований к данной функции будет её измеримость, что служит для отсеивания тех случаев, когда значения данной функции $\text{[math]}$ бесконечно чувствительны к малейшим изменениям в исходах случайного эксперимента. Во многих практических случаях можно рассматривать случайную величину как произвольную функцию из $\text{[math]}$ в $\text{[math]}$ .

В комбинаторике перестано́вкой заданного конечного множества $\text{[math]}$ называется произвольный упорядоченный набор всех элементов $\text{[math]}$ . Группируя эти элементы в разном порядке, можно получить различные перестановки. Всего из множества с $\text{[math]}$ элементами можно получить $\text{[math]}$ различных перестановок.

Корреля́ция, или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин, при этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Норма́льное распределе́ние, также называемое распределением Гаусса или Гаусса — Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

\text{[math]}

где параметр

\text{[math]}

— математическое ожидание, медиана и мода распределения, а параметр

\text{[math]}

— среднеквадратическое отклонение,

\text{[math]}

— дисперсия распределения.

<span class="mw-page-title-main">Случайный процесс</span>

Случа́йный проце́сс в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.

<span class="mw-page-title-main">Геометрическое распределение</span>

Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

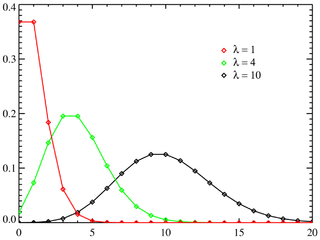
Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Га́мма-распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр $\text{[math]}$ принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.

<span class="mw-page-title-main">Закон больших чисел</span> математический принцип

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Стационарность — свойство процесса не менять свои характеристики со временем. Имеет смысл в нескольких разделах науки.

Эргодическая теорема Биркгофа — Хинчина утверждает, что для динамической системы, сохраняющей меру, и интегрируемой по этой мере функции на пространстве для почти всех начальных точек соответствующие им временны́е средние сходятся. Более того, если инвариантная мера эргодична, то для почти всех начальных точек предел один и тот же — интеграл функции по данной мере. Этот принцип формулируется как «временно́е среднее для почти всех начальных точек равно пространственному».

Множественный коэффициент корреляции - Характеризует тесноту линейной корреляционной связи между одной случайной величиной и некоторым множеством случайных величин. Более точно, если (ξ₁,ξ₂,...,ξ_k) - случайный вектор из R^k, тогда коэффициент множественной корреляции $\text{[math]}$ между ξ₁ и ξ₂,...,ξ_k численно равен коэффициенту парной линейной корреляции между величиной ξ₁ и её наилучшей линейной аппроксимацией $\text{[math]}$ по переменным ξ₂...,ξ_k, которая представляет собой линейную регрессию ξ₁ на ξ₂,...,ξ_k.

Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0..

Статистическая оценка — это статистика, которая используется для оценивания неизвестных параметров распределений случайной величины.

Количество степеней свободы — это количество значений в итоговом вычислении статистики, способных варьироваться. Иными словами, количество степеней свободы показывает размерность вектора из случайных величин, количество «свободных» величин, необходимых для того, чтобы полностью определить вектор.

Дискретная случайная величина — случайная величина, множество значений которой конечно или счётно. Значения дискретной случайной величины не содержат какой-либо непрерывный интервал на числовой прямой.

Теорема Колмогорова о двух рядах в теории вероятностей задаёт достаточное условие сходимости с вероятностью единица ряда независимых случайных величин. Теорема Колмогорова о двух рядах может быть использована для доказательства усиленного закона больших чисел.

Для сходимости с вероятностью единица ряда $\text{[math]}$ из независимых случайных величин достаточно, чтобы одновременно сходились два ряда: $\text{[math]}$ и $\text{[math]}$ . Если к тому же $\text{[math]}$ , то это условие является и необходимым.

K-распределение — в теории вероятности и статистике семейство трёхпараметрических непрерывных вероятностных распределений. Возникает при суперпозиции двух гамма-распределений. В каждом случае производится репараметризация гамма-распределения, и параметрами распределения являются:

среднее значение распределения;
обычные параметры формы.

Теорема Райкова — oбратное утверждение к следующему наблюдению если случайные величины $\text{[math]}$ и $\text{[math]}$ независимы и распределены по закону Пуассона, то их сумма также распределена по закону Пуассона. .

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.