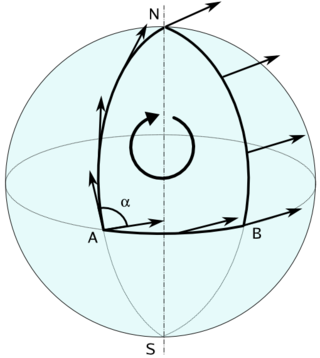
Ковариантная производная — обобщение понятия производной для тензорных полей на многообразиях. Понятие ковариантной производной тесно связано с понятием аффинной связности.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.
Пространственная форма — связное полное риманово многообразие постоянной секционной кривизны 
.
Геодези́ческая — кривая определённого типа, обобщение понятия «прямая» для искривлённых пространств.
Внутренняя метрика — метрика в пространстве, определяемая с помощью функционала длины, как инфимум длин всех путей (кривых), соединяющих данную пару точек.
Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью.
Геодезическая кривизна 
кривой 
в римановой геометрии измеряет, насколько далеко кривая отличается от геодезической. Например, для 1D кривой на 2D поверхности, вложенной в 3D пространство, это кривизна кривой, спроецированной на плоскость, касательную к поверхности. Более обще, в заданном многообразии 
геодезическая кривизна ― это обычная кривизна кривой . Однако если кривая лежит в подмногообразии 
многообразия , геодезическая кривизна относится к кривизне в , и она отличается в общем виде от кривизны в объемлющем многообразии . (Объемлющая) кривизна кривой зависит от двух факторов ― кривизны подмногообразия в направлении , которая зависит только от направления кривой и кривизны в многообразии , которая является величиной второго порядка. Связь между ними ― 
. В частности, геодезические на имеют нулевую геодезическую кривизну («прямые»), так что 
.
Экспоненциальное отображение — обобщение экспоненциальной функции в римановой геометрии.
Лемма Синга — ключевое утверждение о стабильности замкнутых геодезических в римановых многообразиях с положительной секционной кривизной.
Теорема сравнения Рауха — фундаментальный результат римановой геометрии. Доказана Раухом.
Поле Якоби — векторное поле вдоль геодезической в римановом многообразии, описывающие разницу между этой геодезической и «бесконечно близкой» ей геодезической. Можно сказать, что все поля Якоби вдоль геодезической образуют касательное пространство к ней в пространстве всех геодезических.
Радиус инъективности — размер максимальной проколотой окрестности точки полного риманова многообразия, на которой расстояние до этой точки является гладкой функцией.
Замкнутая геодезическая на римановом многообразии — это геодезическая, которая образует простую замкнутую кривую. Её можно формализовать как проекцию замкнутой орбиты геодезического потока на касательное пространство многообразия.
Модулярная кривая 
— это риманова поверхность или соответствующая алгебраическая кривая, построенная как фактор комплексной верхней половины плоскости H по конгруэнтной подгруппе 
модулярной группы целочисленных 2×2 матриц SL(2, Z). Термин модулярная кривая может также использоваться для ссылок на компактифицированные модулярные кривые 
, которые являются компактификациями, полученными добавлением конечного числа точек к фактору. Точки модулярной кривой параметризуют классы изоморфизмов эллиптических кривых, вместе с некоторой дополнительной структурой, зависящей от группы . Эта интерпретация позволяет дать чисто алгебраическое определение модулярных кривых без ссылок на комплексные числа, и, более того, доказывает, что модулярные кривые являются полем определения либо над полем Q рациональных чисел, либо над круговым полем. Последний факт и его обобщения имеют фундаментальную важность в теории чисел.
Голоно́ми́я — один из инвариантов связности в расслоении над гладким многообразием, сочетающий свойства кривизны и монодромии, и имеющий важное значение как в геометрии, так и геометризированных областях естествознания, таких как теория относительности и теория струн. Обыкновенно речь идёт о голономии связностей в векторном расслоении, хотя в равной степени имеет смысл говорить о голономии связности в главном расслоении или даже голономии связности Эресманна в локально тривиальном топологическом расслоении.
Тор Клифтона — Поля — пример компактного лоренцева многообразия, не являющегося геодезически полным. Пример показывает, что теорема Хопфа — Ринова не обобщается на псевдоримановы многообразия. Этот пример был построен Йитоном Клифтоном и Уильямом Полем в 1962 году.
