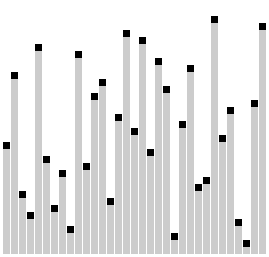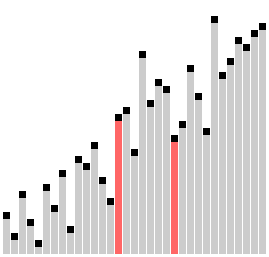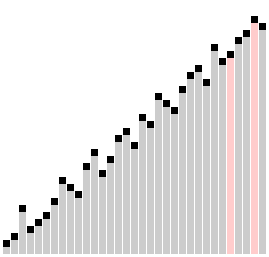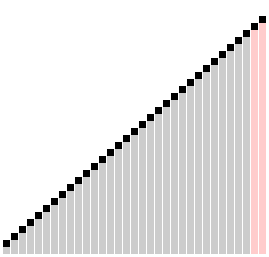
Сортировка Шелла

Сортировка Шелла
Сортировка с шагами 23, 10, 4, 1.
Автор	Дональд Шелл[1]
Предназначение	Алгоритм сортировки
Структура данных	Массив
Худшее время	${\displaystyle O(n^{2})}$
Лучшее время	${\displaystyle O(n\log ^{2}n)}$
Среднее время	зависит от выбранных шагов
Затраты памяти	${\displaystyle O(n)}$ всего, ${\displaystyle O(1)}$ дополнительно

Сортировка Шелла (англ. Shell sort) — алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и на определённом расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными «грубыми» проходами. Аналогичный метод усовершенствования пузырьковой сортировки называется сортировка расчёской.

При сортировке Шелла сначала сравниваются и сортируются между собой значения, стоящие один от другого на некотором расстоянии ${\displaystyle d}$ (о выборе значения ${\displaystyle d}$ см. ниже). После этого процедура повторяется для некоторых меньших значений ${\displaystyle d}$, а завершается сортировка Шелла упорядочиванием элементов при ${\displaystyle d=1}$ (то есть обычной сортировкой вставками). Эффективность сортировки Шелла в определённых случаях обеспечивается тем, что элементы «быстрее» встают на свои места (в простых методах сортировки, например, пузырьковой, каждая перестановка двух элементов уменьшает количество инверсий в списке максимум на 1, а при сортировке Шелла это число может быть больше).

Невзирая на то, что сортировка Шелла во многих случаях медленнее, чем быстрая сортировка, она имеет ряд преимуществ:

• отсутствие потребности в памяти под стек;
• отсутствие деградации при неудачных наборах данных — быстрая сортировка легко деградирует до ${\displaystyle O(n^{2})}$, что хуже, чем худшее гарантированное время для сортировки Шелла.

Сортировка Шелла была названа в честь её изобретателя — Дональда Шелла, который опубликовал этот алгоритм в 1959 году.

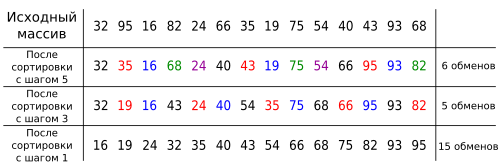
Пусть дан список ${\displaystyle A=(32,95,16,82,24,66,35,19,75,54,40,43,93,68)}$ и выполняется его сортировка методом Шелла, а в качестве значений ${\displaystyle d}$ выбраны ${\displaystyle 5,3,1}$.

На первом шаге сортируются подсписки ${\displaystyle A}$, составленные из всех элементов ${\displaystyle A}$, различающихся на 5 позиций, то есть подсписки ${\displaystyle A_{5,1}=(32,66,40)}$, ${\displaystyle A_{5,2}=(95,35,43)}$, ${\displaystyle A_{5,3}=(16,19,93)}$, ${\displaystyle A_{5,4}=(82,75,68)}$, .${\displaystyle A_{5,5}=(24,54)}$

В полученном списке на втором шаге вновь сортируются подсписки из отстоящих на 3 позиции элементов.

Процесс завершается обычной сортировкой вставками получившегося списка.

Среднее время работы алгоритма зависит от длин промежутков — ${\displaystyle d}$, на которых будут находиться сортируемые элементы исходного массива ёмкостью ${\displaystyle N}$ на каждом шаге алгоритма. Существует несколько подходов к выбору этих значений:

• первоначально используемая Шеллом последовательность длин промежутков: ${\displaystyle d_{1}=N/2,d_{i}=d_{i-1}/2,d_{k}=1}$ в худшем случае, сложность алгоритма составит ${\displaystyle O(N^{2})}$;
• предложенная Хиббардом последовательность: все значения ${\displaystyle 2^{i}-1\leq N,i\in \mathbb {N} }$; такая последовательность шагов приводит к алгоритму сложностью ${\displaystyle O(N^{3/2})}$;
• предложенная Седжвиком последовательность: ${\displaystyle d_{i}=9\cdot 2^{i}-9\cdot 2^{i/2}+1}$, если i четное и ${\displaystyle d_{i}=8\cdot 2^{i}-6\cdot 2^{(i+1)/2}+1}$, если i нечетное. При использовании таких приращений средняя сложность алгоритма составляет: ${\displaystyle O(n^{7/6})}$, а в худшем случае порядка ${\displaystyle O(n^{4/3})}$. При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.^[2];
• предложенная Праттом последовательность: все значения ${\displaystyle 2^{i}\cdot 3^{j}\leq N/2,i,j\in \mathbb {N} }$; в таком случае сложность алгоритма составляет ${\displaystyle O(N\log ^{2}N)}$;
• эмпирическая последовательность Марцина Циура (последовательность A102549 в OEIS): ${\displaystyle d\in \left\{1,4,10,23,57,132,301,701,1750\right\}}$; является одной из лучших для сортировки массива ёмкостью приблизительно до 4000 элементов.^[3];
• эмпирическая последовательность, основанная на числах Фибоначчи: ${\displaystyle d\in \left\{F_{n}\right\}}$.

template<typename RandomAccessIterator, typename Compare>
void shell_sort( RandomAccessIterator first, RandomAccessIterator last, Compare comp )
{
    for( auto d = ( last - first ) / 2; d != 0; d /= 2 )
    //нужен цикл для first = a[0..d-1]
        for( auto i = first + d; i != last; ++i )
            for( auto j = i; j - first >= d && comp( *j, *( j - d ) ); j -= d )
                std::swap( *j, *( j - d ) );
}

void shell_sort(int *array, int size) {
    for (int s = size / 2; s > 0; s /= 2) {
        for (int i = s; i < size; ++i) {
            for (int j = i - s; j >= 0 && array[j] > array[j + s]; j -= s) {
                int temp = array[j];
                array[j] = array[j + s];
                array[j + s] = temp;
            }
        }
    }
}

void shell_sort(List<Integer> array) {
        for (int s = array.size() / 2; s > 0; s /= 2)
            for (int i = s; i < array.size(); ++i)
                for (int j = i - s; j >= 0 && array.get(j) > array.get(j + s); j -= s) Collections.swap(array, j, j + s);
}

def shell_sort(data: list[int]) -> list[int]:
    last_index = len(data)
    step = len(data)//2
    while step > 0:
        for i in range(step, last_index, 1):
            j = i
            delta = j - step
            while delta >= 0 and data[delta] > data[j]:
                data[delta], data[j] = data[j], data[delta]
                j = delta
                delta = j - step
        step //= 2
    return data

• Дональд Кнут. Искусство программирования. Том 3. Сортировка и поиск, 2-е изд. Гл. 5.2.1. ISBN 5-8459-0082-4
• Анимированное представление алгоритма сортировки Шелла
• Представление алгоритма сортировки Шелла в виде танца (видео)