Сортировка с помощью двоичного дерева

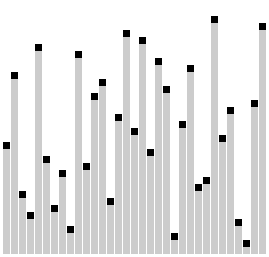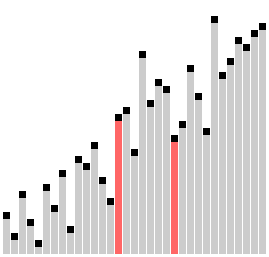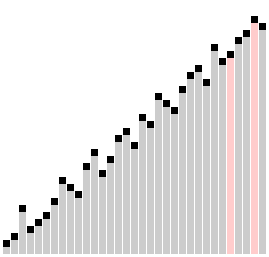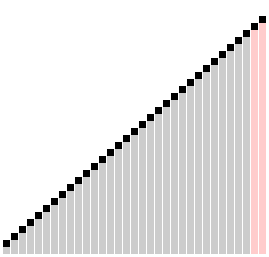
Сортировка с помощью двоичного дерева (сортировка двоичным деревом, сортировка деревом, древесная сортировка, сортировка с помощью бинарного дерева, англ. tree sort) — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения из потока (например, файла, сокета или консоли).
Алгоритм
- Построение двоичного дерева.
- Сборка результирующего массива путём обхода узлов в необходимом порядке следования ключей.
Эффективность
Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка . Соответственно, для n объектов сложность будет составлять , что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать , что может привести к общей сложности порядка .
При физическом развёртывании древовидной структуры в памяти требуется не менее чем ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.
Примеры реализации
В простой форме функционального программирования на Haskell данный алгоритм будет выглядеть так:
data Tree a = Leaf | Node (Tree a) a (Tree a)
insert :: Ord a => a -> Tree a -> Tree a
insert x Leaf = Node Leaf x Leaf
insert x (Node t y t') | x <= y = Node (insert x t) y t'
insert x (Node t y t') | x > y = Node t y (insert x t')
flatten :: Tree a -> [a]
flatten Leaf = []
flatten (Node t x t') = flatten t ++ [x] ++ flatten t'
treesort :: Ord a => [a] -> [a]
treesort = flatten . foldr insert Leaf
Реализация на C++14:
#include <memory>
#include <cassert>
#include <algorithm>
#include <vector>
#include <iostream>
using namespace std;
// класс, представляющий бинарное дерево
class BinaryTree
{
protected:
// узел бинарного дерева
struct BinaryTreeNode
{
shared_ptr<BinaryTreeNode> left, right; // левое и правое поддерево
int key; // ключ
};
shared_ptr<BinaryTreeNode> m_root; // корень дерева
protected:
// рекурсивная процедура вставки ключа
// cur_node - текущий узел дерева, с которым сравнивается вставляемый узел
// node_to_insert - вставляемый узел
void insert_recursive(const shared_ptr<BinaryTreeNode>& cur_node, const shared_ptr<BinaryTreeNode>& node_to_insert)
{
assert(cur_node != nullptr);
// сравнение
bool insertIsLess = node_to_insert->key < cur_node->key;
if(insertIsLess)
{
// вставка в левое поддерево
if(cur_node->left == nullptr)
cur_node->left = node_to_insert;
else
insert_recursive(cur_node->left, node_to_insert);
}
else
{
// вставка в правое поддерево
if(cur_node->right == nullptr)
cur_node->right = node_to_insert;
else
insert_recursive(cur_node->right, node_to_insert);
}
}
public:
void insert(int key)
{
shared_ptr<BinaryTreeNode> node_to_insert(new BinaryTreeNode);
node_to_insert->key = key;
if(m_root == nullptr)
{
m_root = node_to_insert;
return;
}
insert_recursive(m_root, node_to_insert);
}
public:
typedef function<void(int key)> Visitor;
protected:
// рекурсивная процедура обхода дерева
// cur_node - посещаемый в данный момент узел
void visit_recursive(const shared_ptr<BinaryTreeNode>& cur_node, const Visitor& visitor)
{
assert(cur_node != nullptr);
// сначала посещаем левое поддерево
if(cur_node->left != nullptr)
visit_recursive(cur_node->left, visitor);
// посещаем текущий элемент
visitor(cur_node->key);
// посещаем правое поддерево
if(cur_node->right != nullptr)
visit_recursive(cur_node->right, visitor);
}
public:
void visit(const Visitor& visitor)
{
if(m_root == nullptr)
return;
visit_recursive(m_root, visitor);
}
};
int main()
{
BinaryTree tree;
// добавление элементов в дерево
vector<int> data_to_sort = {10, 2, 7, 3, 14, 7, 32};
for(int value : data_to_sort)
{
tree.insert(value);
}
// обход дерева
tree.visit([](int visited_key)
{
cout<<visited_key<<" ";
});
cout<<endl;
// результат выполнения: 2 3 7 7 10 14 32
return 0;
}
Полная реализация на C++11:
#include <algorithm>
#include <cstddef>
#include <utility>
template<typename T>
void tree_sort(T array[], std::size_t size) noexcept
{
struct tree_t
{
tree_t(T &&_value = T())
{
left = right = nullptr;
value = std::forward<T>(_value);
}
T* operator()(T array[])
{
if (this->left) array = this->left->operator()(array);
*array++ = std::move(this->value);
if (this->right) array = this->right->operator()(array);
return array;
}
tree_t *left, *right;
T value;
} root(std::move(array[0]));
for (std::size_t idx = 1; idx < size; idx++)
{
bool inserted = false;
tree_t *p_root = &root;
while (!inserted)
{
if (array[idx] < p_root->value)
{
if (p_root->left) p_root = p_root->left;
else
{
p_root->left = new tree_t(std::move(array[idx]));
inserted = true;
}
}
else
{
if (p_root->right) p_root = p_root->right;
else
{
p_root->right = new tree_t(std::move(array[idx]));
inserted = true;
}
}
}
}
root(array);
}
Пример создания бинарного дерева и сортировки на языке Java:
// Скомпилируйте и введите java TreeSort
class Tree {
public Tree left; // левое и правое поддеревья и ключ
public Tree right;
public int key;
public Tree(int k) { // конструктор с инициализацией ключа
key = k;
}
/* insert (добавление нового поддерева (ключа))
сравнить ключ добавляемого поддерева (К) с ключом корневого узла (X).
Если K>=X, рекурсивно добавить новое дерево в правое поддерево.
Если K<X, рекурсивно добавить новое дерево в левое поддерево.
Если поддерева нет, то вставить на это место новое дерево
*/
public void insert( Tree aTree) {
if ( aTree.key < key )
if ( left != null ) left.insert( aTree );
else left = aTree;
else
if ( right != null ) right.insert( aTree );
else right = aTree;
}
/* traverse (обход)
Рекурсивно обойти левое поддерево.
Применить функцию f (печать) к корневому узлу.
Рекурсивно обойти правое поддерево.
*/
public void traverse(TreeVisitor visitor) {
if ( left != null)
left.traverse( visitor );
visitor.visit(this);
if ( right != null )
right.traverse( visitor );
}
}
interface TreeVisitor {
public void visit(Tree node);
};
class KeyPrinter implements TreeVisitor {
public void visit(Tree node) {
System.out.println( " " + node.key );
}
};
class TreeSort {
public static void main(String args[]) {
Tree myTree;
myTree = new Tree( 7 ); // создать дерево (с ключом)
myTree.insert( new Tree( 5 ) ); // присоединять поддеревья
myTree.insert( new Tree( 9 ) );
myTree.traverse(new KeyPrinter());
}
}