Дельто́ид — четырёхугольник, у которого по две смежные стороны равны ; если бо́льшая пара смежных сторон изображена вверх, то очертания фигуры напоминают заглавную греческую букву Δ. В ранней литературе иногда также называется ромбоидом, однако в современной планиметрии ромбоидом обычно считается параллелограмм, не являющийся прямоугольником или ромбом.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.
Геронов треугольник — треугольник, стороны и площадь которого являются целыми числами. Героновы треугольники названы в честь греческого математика Герона. Термин иногда понимается несколько шире и распространяется на треугольники, имеющие рациональные стороны и площадь.

Окта́эдр — многогранник с восемью гранями.

Медиа́на треуго́льника ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине. Иногда медианой называют также прямую, содержащую этот отрезок, а иногда длину этого отрезка. Точка пересечения медианы со стороной треугольника называется основанием медианы.

Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии.

Правильный треугольник — треугольник, все стороны которого равны между собой, как следствие, все углы также равны и составляют 60°; дважды равнобедренный треугольник; правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Символ Шлефли —  .
.

Равнобедренный треугольник — треугольник, в котором две стороны имеют равную длину. Боковыми называются равные стороны, а третья сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.

Фронто́н — завершение фасада здания, портика, колоннады, ограниченное двумя скатами крыши по бокам и карнизом у основания.

Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью.
Точки Наполеона в геометрии — пара специальных точек на плоскости треугольника. Легенда приписывает обнаружение этих точек французскому императору Наполеону I, однако его авторство сомнительно. Точки Наполеона относятся к замечательным точкам треугольника и перечислены в Энциклопедии центров треугольника как точки X(17) и X(18).

Точки Торричелли — две точки, из которых все стороны треугольника видны либо под углом в 60°, либо под углом в 120°. Эти точки в треугольнике — «парные». Иногда эти точки называют точками Ферма или точками Ферма-Торричелли.
- Две Точки Торричелли — это точки пересечения отрезков, соединяющих вершины треугольника:
- c соответствующими свободными вершинами равносторонних треугольников, построенных на противолежащих сторонах треугольника (наружу) — первая точка Торричелли
- с соответствующими свободными вершинами правильных треугольников, построенных на противолежащих сторонах внутрь треугольника — вторая точка Торричелли.
Треугольная призма — призма с тремя боковыми гранями. Этот многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны. Прямая треугольная призма имеет прямоугольные боковые стороны, в противном случае призма называется косой.

Делящаяся плитка — понятие геометрии мозаик, фигура, которую можно разрезать на меньшие копии самой фигуры. В 2012 обобщение делящихся мозаик с названием self-tiling tile set было предложено английским математиком Ли Сэлоусом в журнале Mathematics Magazine.

Дельтаэдр — это многогранник, все грани которого являются правильными треугольниками. Название взято от греческой заглавной буквы дельта, которая имеет форму равностороннего треугольника. Существует бесконечно много дельтаэдров, но из них только восемь выпуклы, и они имеют 4, 6, 8, 10, 12, 14, 16 и 20 граней.

Икосаэдр — это многогранник с 20 гранями.

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый внутренний угол равен 45°:


Триангуляция — способ пропорционирования здания на основе системы равносторонних или равнобедренных треугольников.

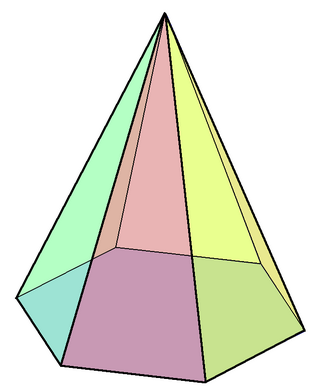
Пятиуго́льная пирами́да — пирамида, имеющая пятиугольное основание.