Спичечный граф

В теории графов спичечным графом называется граф, который можно нарисовать на плоскости таким образом, что все его рёбра представляют собой отрезки прямой длиной единица и рёбра не пересекаются. Таким образом, этот граф имеет вложение в плоскость одновременно в виде графа единичных расстояний и планарного графа. Говоря неформально, спичечный граф можно выложить непересекающимися на плоской поверхности спичками, откуда и название^[1].

Много исследований спичечных графов касается регулярных графов, в которых каждая вершина имеет одинаковое число соседей. Это число называется степенью графа.

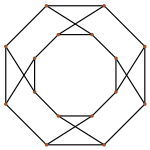
Известно, что существуют спичечные графы всех степеней вплоть до четвёртой. Полные графы с одной, двумя и тремя вершинами (отдельная вершина, ребро и треугольник) являются спичечными графами, 0-, 1- и 2-регулярными соответственно. Наименьший 3-регулярный спичечный граф образуется двумя копиями ромбов, расположенных так, что соответствующие вершины располагаются на единичном расстоянии. Его двойное двудольное покрытие — это граф 8-угольной призмы с пересечениями^[1].

В 1986 году Хейко Харборт представил граф, который получил его имя — граф Харборта. Имея 104 ребра и 52 вершины, этот граф является наименьшим известным примером 4-регулярного спичечного графа^[2]. Граф является жёстким^[3].

Невозможно для регулярного спичечного графа иметь степень больше чем четыре^[4].

Как показали Курц и Мазуколо^[5], наименьший 3-регулярный спичечный граф без треугольников (обхват ≥ 4) имеет 20 вершин. Кроме того, они представили наименьший известный пример 3-регулярного спичечного графа с обхватом 5 (180 вершин).

Проверка, можно ли представить заданный неориентированный планарный граф в виде спичечного графа, является NP-трудной задачей^[6][7]

Число различных (с точностью до изоморфизма) спичечных графов известно вплоть до десяти рёбер^[8][9]:

1, 1, 3, 5, 12, 28, 74, 207, 633, 2008, …